题目描述

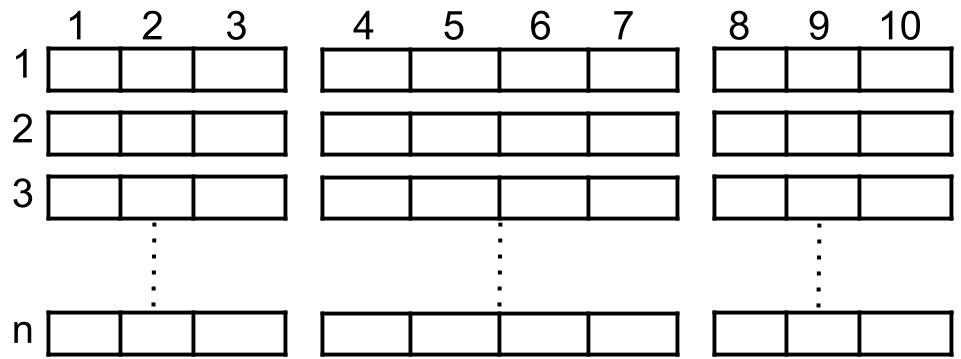
如上图所示，电影院的观影厅中有 n 行座位，行编号从 1 到 n ，且每一行内总共有 10 个座位，列编号从 1 到 10 。

给你数组 reservedSeats ，包含所有已经被预约了的座位。比如说，researvedSeats[i]=[3,8] ，它表示第 3 行第 8 个座位被预约了。

请你返回 最多能安排多少个 4 人家庭 。4 人家庭要占据 同一行内连续 的 4 个座位。隔着过道的座位（比方说 [3,3] 和 [3,4]）不是连续的座位，但是如果你可以将 4 人家庭拆成过道两边各坐 2 人，这样子是允许的。

样例

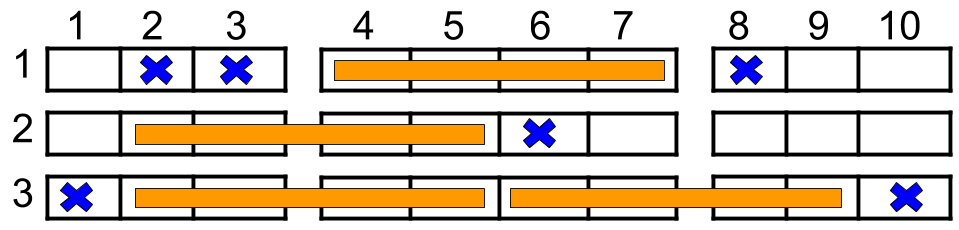
输入：n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
输出：4
解释：上图所示是最优的安排方案，总共可以安排 4 个家庭。蓝色的叉表示被预约的座位，橙色的连续座位表示一个 4 人家庭。

输入：n = 2, reservedSeats = [[2,1],[1,8],[2,6]]
输出：2

输入：n = 4, reservedSeats = [[4,3],[1,4],[4,6],[1,7]]
输出：4

提示：

• 1 <= n <= 10^9

• 1 <= reservedSeats.length <= min(10*n, 10^4)

• reservedSeats[i].length == 2

• 1 <= reservedSeats[i][0] <= n

• 1 <= reservedSeats[i][1] <= 10

• 所有 reservedSeats[i] 都是互不相同的。

算法分析

模拟

• 1、用哈希表存储每一行有哪些位置被预约

• 2、先算出被预约过的每一行能坐多少个家庭，即res，枚举哈希表中被预约过的每一行，left,right,middle分别记录的是左边，右边，中间能否坐满一个家庭，

  • 1、若 left 和 right 均为 true ，表示能坐 2 个家庭

  • 2、不满足1的条件下，若 left 和 right 任意一个是 true ，表示能坐 1 个家庭

  • 3、不满足1、2的条件下，若 middle 是 true ，表示能坐满 1 个家庭

• 3、结果为n - map.size + res

时间复杂度 $O(给的数组长度)$

Java 代码

class Solution {
    public int maxNumberOfFamilies(int n, int[][] reservedSeats) {
        Map<Integer, HashSet<Integer>> map = new HashMap<Integer,HashSet<Integer>>();
        int res = 0;
        for(int i = 0;i < reservedSeats.length;i ++)
        {
            int row = reservedSeats[i][0];
            int col = reservedSeats[i][1];
            if(!map.containsKey(row)) map.put(row, new HashSet<Integer>());
            map.get(row).add(col);
        }
        for(Map.Entry<Integer, HashSet<Integer>> entry : map.entrySet())
        {
            HashSet t = entry.getValue();
            int cnt = 0;
            boolean left = false,right = false,middle = false;
            if(!t.contains(2) && !t.contains(3) && !t.contains(4) && !t.contains(5)) left = true;
            if(!t.contains(6) && !t.contains(7) && !t.contains(8) && !t.contains(9)) right = true;
            if(!t.contains(4) && !t.contains(5) && !t.contains(6) && !t.contains(7)) middle = true;
            if(left && right) cnt += 2;
            else if((left || right) || middle) cnt += 1;
            res += cnt;
        }
        return (n - map.size()) * 2 + res;
    }
}