题目描述

给你一个 m x n 的网格 grid。网格里的每个单元都代表一条街道。grid[i][j] 的街道可以是：

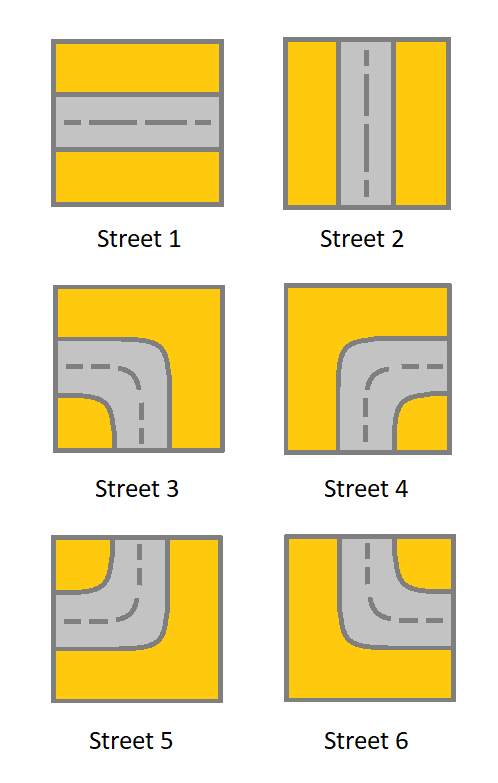
• 1 表示连接左单元格和右单元格的街道。
• 2 表示连接上单元格和下单元格的街道。
• 3 表示连接左单元格和下单元格的街道。
• 4 表示连接右单元格和下单元格的街道。
• 5 表示连接左单元格和上单元格的街道。
• 6 表示连接右单元格和上单元格的街道。

你最开始从左上角的单元格 (0,0) 开始出发，网格中的 有效路径 是指从左上方的单元格 (0, 0) 开始，一直到右下方的 (m - 1,n - 1) 结束的路径。该路径必须只沿着街道走。

注意：你 不能 变更街道。

如果网格中存在有效的路径，则返回 true，否则返回 false。

样例

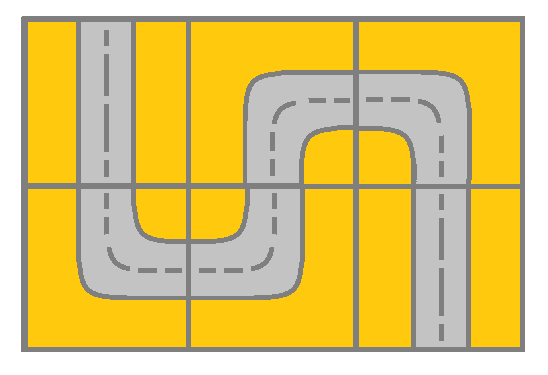
输入：grid = [[2,4,3],[6,5,2]]
输出：true
解释：如图所示，你可以从 (0, 0) 开始，访问网格中的所有单元格并到达 (m - 1, n - 1)。

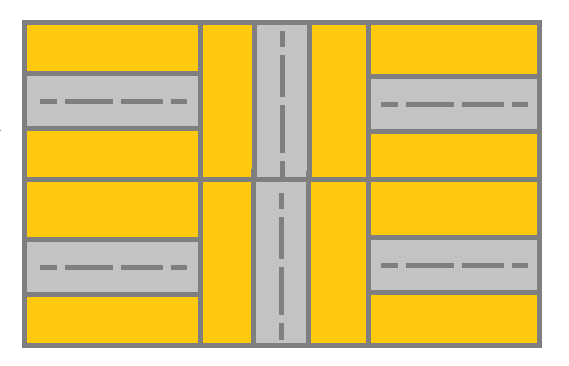
输入：grid = [[1,2,1],[1,2,1]]
输出：false
解释：如图所示，单元格 (0, 0) 上的街道没有与任何其他单元格上的街道相连，你只会停在 (0, 0) 处。

输入：grid = [[1,1,2]]
输出：false
解释：你会停在 (0, 1)，而且无法到达 (0, 2) 。

输入：grid = [[1,1,1,1,1,1,3]]
输出：true

输入：grid = [[2],[2],[2],[2],[2],[2],[6]]
输出：true

限制

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• 1 <= grid[i][j] <= 6

算法

(宽度优先遍历) $O(mn)$

1. 按照规则进行宽度优先遍历。
2. 转移的过程中，需要判断两个点之间是否能互相到达。

时间复杂度

• 每个点最多遍历一次，共有 $O(mn)$ 条边，故总时间复杂度为 $O(mn)$。

空间复杂度

• 需要额外 $O(mn)$ 的空间存储队列和访问标记数组。

C++ 代码

class Solution {
public:
    void add(int x, int y, queue<pair<int, int>> &q, vector<vector<bool>> &vis) {
        if (!vis[x][y]) {
            vis[x][y] = true;
            q.push(make_pair(x, y));
        }
    }

    bool hasValidPath(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();

        vector<vector<bool>> vis(m, vector<bool>(n, false));
        queue<pair<int, int>> q;
        vis[0][0] = true;

        q.push(make_pair(0, 0));

        while (!q.empty()) {
            auto u = q.front();
            q.pop();
            int x = u.first, y = u.second;
            if (x == m - 1 && y == n - 1)
                return true;

            if ((grid[x][y] == 2 || grid[x][y] == 5 || grid[x][y] == 6)
                && x - 1 >= 0
                && (grid[x - 1][y] == 2 || grid[x - 1][y] == 3 || grid[x - 1][y] == 4))
                add(x - 1, y, q, vis);

            if ((grid[x][y] == 1 || grid[x][y] == 3 || grid[x][y] == 5)
                && y - 1 >= 0
                && (grid[x][y - 1] == 1 || grid[x][y - 1] == 4 || grid[x][y - 1] == 6))
                add(x, y - 1, q, vis);

            if ((grid[x][y] == 2 || grid[x][y] == 3 || grid[x][y] == 4)
                && x + 1 < m
                && (grid[x + 1][y] == 2 || grid[x + 1][y] == 5 || grid[x + 1][y] == 6))
                add(x + 1, y, q, vis);

            if ((grid[x][y] == 1 || grid[x][y] == 4 || grid[x][y] == 6)
                && y + 1 < n
                && (grid[x][y + 1] == 1 || grid[x][y + 1] == 3 || grid[x][y + 1] == 5))
                add(x, y + 1, q, vis);
        }

        return false;
    }
};