题目描述

给你一个披萨，它由 3n 块不同大小的部分组成，现在你和你的朋友们需要按照如下规则来分披萨：

• 你挑选 任意 一块披萨。
• Alice 将会挑选你所选择的披萨逆时针方向的下一块披萨。
• Bob 将会挑选你所选择的披萨顺时针方向的下一块披萨。
  *重复上述过程直到没有披萨剩下。

每一块披萨的大小按顺时针方向由循环数组 slices 表示。

请你返回你可以获得的披萨大小总和的最大值。

样例

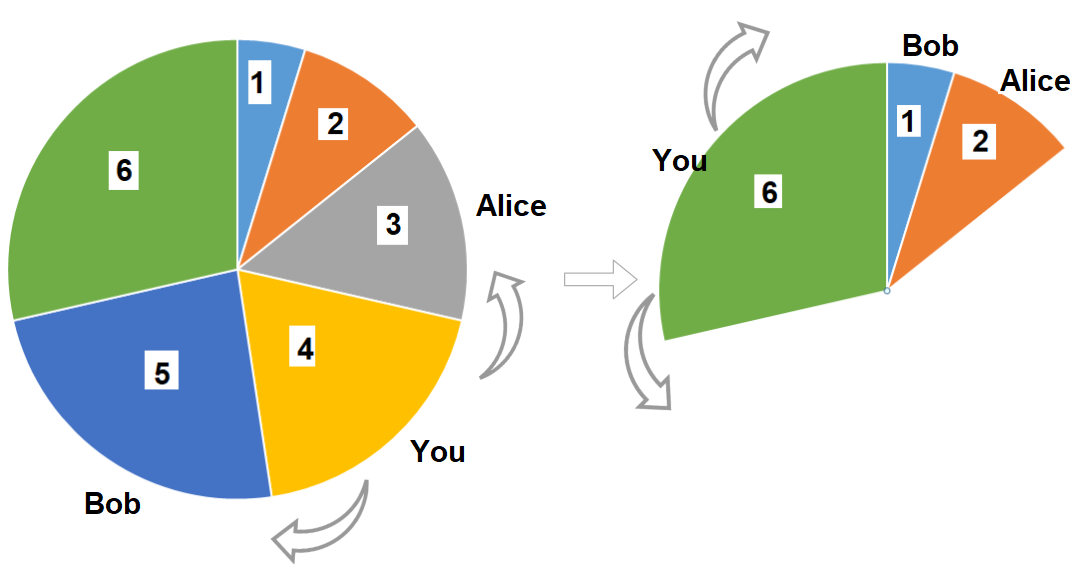
输入：slices = [1,2,3,4,5,6]
输出：10
解释：选择大小为 4 的披萨，Alice 和 Bob 分别挑选大小为 3 和 5 的披萨。
然后你选择大小为 6 的披萨，Alice 和 Bob 分别挑选大小为 2 和 1 的披萨。
你获得的披萨总大小为 4 + 6 = 10。

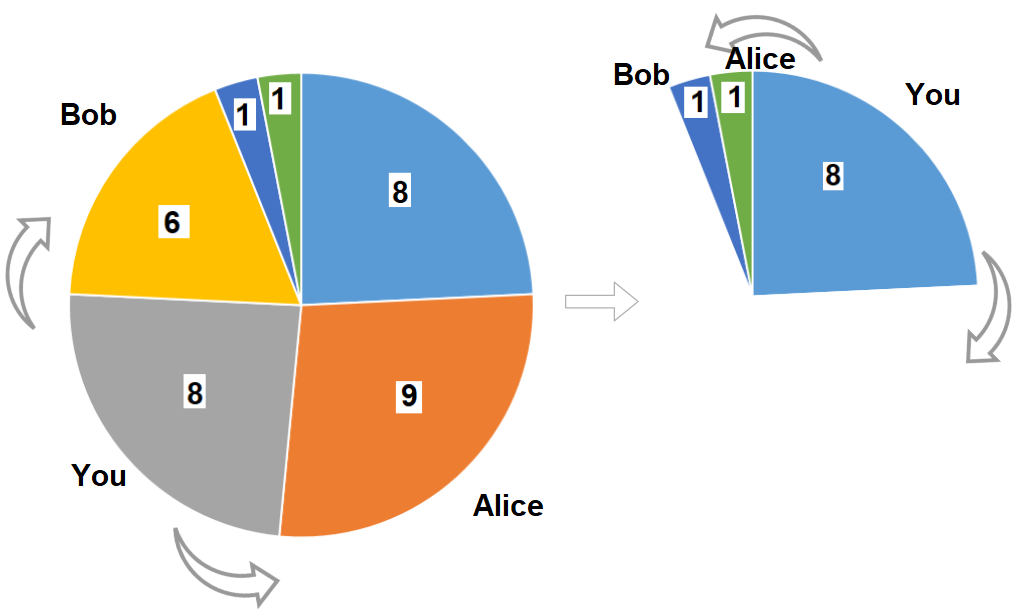
输入：slices = [8,9,8,6,1,1]
输出：16
解释：两轮都选大小为 8 的披萨。
如果你选择大小为 9 的披萨，你的朋友们就会选择大小为 8 的披萨，这种情况下你的总和不是最大的。

输入：slices = [4,1,2,5,8,3,1,9,7]
输出：21

输入：slices = [3,1,2]
输出：3

限制

• 1 <= slices.length <= 500
• slices.length % 3 == 0
• 1 <= slices[i] <= 1000

算法1

(区间动态规划) $O(n^3)$

1. 设状态 $f(i, j)$ 表示分完区间 [i, j] 的披萨能得到的最大总和。其中，区间长度始终为 3 的倍数。
2. 由于这是个环形的问题，所以我们考虑将原数组拷贝一份接在后边，即我们在总长度为 2n 的数组上做动态规划，找到一个总长度为 n 的子问题的最大值。
3. 初始时，$f(i - 1, i + 1) = a[i]$。
4. 转移时，对于当前区间 [i, j]，我们可以考虑将其一分为二，分成两个长度都是 3 的倍数的子区间。还有一类转移是，固定开头和结尾，枚举中点 $k$，$i < k < j$，满足 [i + 1, k - 1] 和 [k + 1, j - 1] 的长度都是 3 的倍数。可以看到，任何一种划分方式都可以由这两类转移得到，故我们取这两类转移的最大值。
5. 最终答案就是 $\max(f(i, i + n - 1))$，其中 $0 \le i < n$。

时间复杂度

• 状态数为 $O(n^2)$，每个状态需要 $O(n)$ 的时间转移，故总时间复杂度为 $O(n^3)$。

空间复杂度

• 需要额外 $O(n^2)$ 的空间。

C++ 代码

class Solution {
public:
    int maxSizeSlices(vector<int>& slices) {
        int n = slices.size();
        vector<int> a(slices);
        a.insert(a.end(), slices.begin(), slices.end());

        vector<vector<int>> f(2 * n + 1, vector<int>(2 * n + 1, 0));
        for (int i = 1; i < 2 * n - 1; i++)
            f[i - 1][i + 1] = a[i];

        for (int len = 6; len <= n; len += 3)
            for (int i = 0; i < 2 * n - len + 1; i++) {
                int j = i + len - 1;

                for (int k = i + 2; k <= j - 3; k += 3)
                    f[i][j] = max(f[i][j], f[i][k] + f[k + 1][j]);

                for (int k = i + 1; k <= j - 1; k += 3)
                    f[i][j] = max(f[i][j], f[i + 1][k - 1] + a[k] + f[k + 1][j - 1]);
            }

        int ans = 0;
        for (int i = 0; i < n; i++)
            ans = max(ans, f[i][i + n - 1]);

        return ans;
    }
};

算法2

(动态规划) $O(n^2)$

1. 这个问题可以转化为，从长度为 n 的环形数组中选择 n/3 个互不相邻的数字。
2. 我们分为两类，一类是不允许取第一个数字，一类是不允许去最后一个数字。
3. 对这两类问题分别做动态规划，此时转换为线性数组上的问题。
4. 下标从 0 开始。设状态 $f(i, j)$ 表示前 $i$ 个数字，取了 $j$ 个数字的最大总和。
5. 转移时，可以取第 $i$ 个数字，也可以不取第 $i$ 个数字，很容易写出转移方程。
6. 最终答案为 $f(n - 1, n / 3)$。

时间复杂度

• 状态数为 $O(n^2)$ 个，转移为常数时间，故总时间复杂度为 $O(n^2)$。

空间复杂度

• 需要额外 $O(n^2)$ 的空间存储状态。

C++ 代码

class Solution {
public:
    int solve(const vector<int>& nums) {
        int n = nums.size();
        vector<vector<int>> f(n, vector<int>(n / 3 + 1, INT_MIN));

        f[0][0] = 0;
        f[0][1] = nums[0];
        for (int i = 1; i < n; i++) {
            for (int j = 0; j <= n / 3; j++) {
                f[i][j] = f[i - 1][j];
                if (j == 1) f[i][1] = max(f[i][1], nums[i]);
                if (i >= 2 && j >= 1) f[i][j] = max(f[i][j], f[i - 2][j - 1] + nums[i]);
            }
        }

        return f[n - 1][n / 3];
    }

    int maxSizeSlices(vector<int>& slices) {
        vector<int> nums(slices);
        nums[0] = slices.back() = INT_MIN;
        return max(solve(slices), solve(nums));
    }
};