算法提高课汇总

理解题意

若数字$N$满足条件, 则$N = \sum_{i} B^i$, 即$N$的$B$进制表示只有$0$和$1$, 且$1$的个数为$K$.

数位$DP$

数位$DP$问题一般形式: 在某区间满足某种性质的数字个数.

解题技巧$1$

类似前缀和思想, 题目问某区间满足性质数字个数$f([X, Y]) = f’(Y) - f’(X - 1)$, 其中
$f’(N)$表示$0\sim N$中满足性质的数字个数.

解题技巧$2$

按$N$的数位从大到小分类讨论(集合划分), 主要考虑$\le N$限制, 以及满足性质的情况.

回到本题, 假设$N$的$B$进制表示为$N = a_{n-1}, a_{n-2}, …, a_0$. 首先分类考虑最高位:

• 最高位数字为$0\sim a_{n-1} - 1$, 此时$0\sim n-2$位数字任取都不会超过$N$($I’am free!$),
  问题转变为组合问题: 在剩余$n - 1$位中选择$K$或$K-1$位为$1$的所有可能情况, 可直接求解.

• 最高位数字为$a_{n - 1}$, 后续数字若任意选择可能会超过$N$, 需要进一步讨论.

在最高位为$a_{n - 1}$的条件下我们继续向下讨论, 直到遇到$a_0$为止.

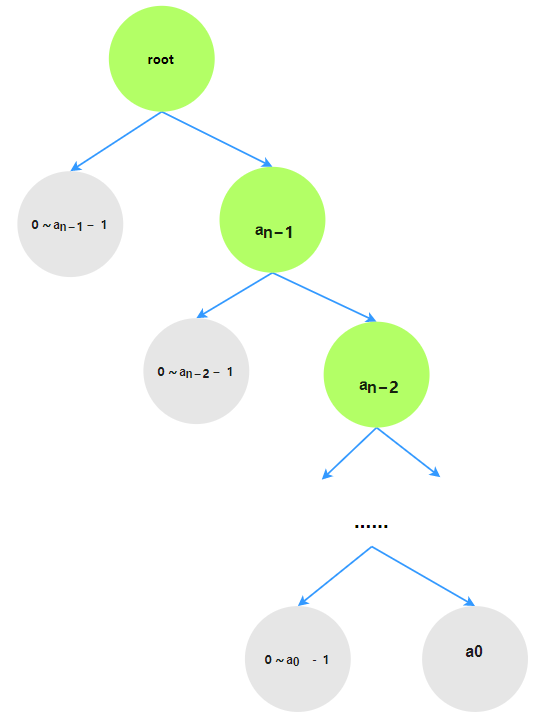
最后综合所有叶子节点的计算结果.

具体实现

注意本题可能出现提前结束的情况(提前遇到叶节点), 以$a_{n - 1}$为例:

• $a_{n - 1} = 0$, 则其不存在左子树, 继续向下讨论.

• $a_{n - 1} = 1$, 存在$a_{n - 1} = 0$的左子树, 继续向下讨论.

• $a_{n - 1}\gt 1$, 存在$a_{n - 1} = 0, 1$的左子树, 此时右子树的$a_{n - 1}$不为$0$或$1$,
  向下讨论也不存在满足条件的数字 — 只能由$0$和$1$组成, 所以可以提前结束.

具体代码

#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 35;

int K, B;
int f[N][N]; //组合数

void init()
{//递推计算组合数
    for ( int i = 0; i < N; i ++ )
        for ( int j = 0; j <= i; j ++ )
            if ( !j )   f[i][j] = 1;
            else    f[i][j] = f[i - 1][j] + f[i - 1][j - 1];
}

int dp(int n)
{
    if ( !n )   return 0; //l - 1最小到达0, 需要特别讨论: 由于K > 1, 所以0一定不满足条件

    vector<int> nums; //按位存储
    while ( n ) nums.push_back( n % B ), n /= B;

    int res = 0; //最终结果, 综合所有叶节点
    int last = 0; //之前确定的位数的信息, 这里是之前确定位数1的个数
    for ( int i = nums.size() - 1; i >= 0; i -- ) //从大到小按位讨论
    {
        int x = nums[i];
        if ( x )
        {//存在左子树
            res += f[i][K - last]; //a(i) = 0的左子树
            if ( x > 1 )
            {//存在a(i) = 1的左子树
                //需要判断是否还可以填1
                if ( K - last - 1 >= 0 )    res += f[i][K - last - 1];
                break; //a(i) > 1, 提前退出
            }
            else
            {
                last ++ ;
                if ( last > K ) break; //后续无合法数字
            }
        }
        //最后一个叶子节点 实际表示n的B进制是否合法 之前讨论的都是0 ~ n - 1
        if ( !i && last == K )  res ++ ; 
    }
    return res;
}

int main()
{
    int l, r;
    cin >> l >> r >> K >> B;

    init();
    cout << dp(r) - dp(l - 1) << endl;

    return 0;
}