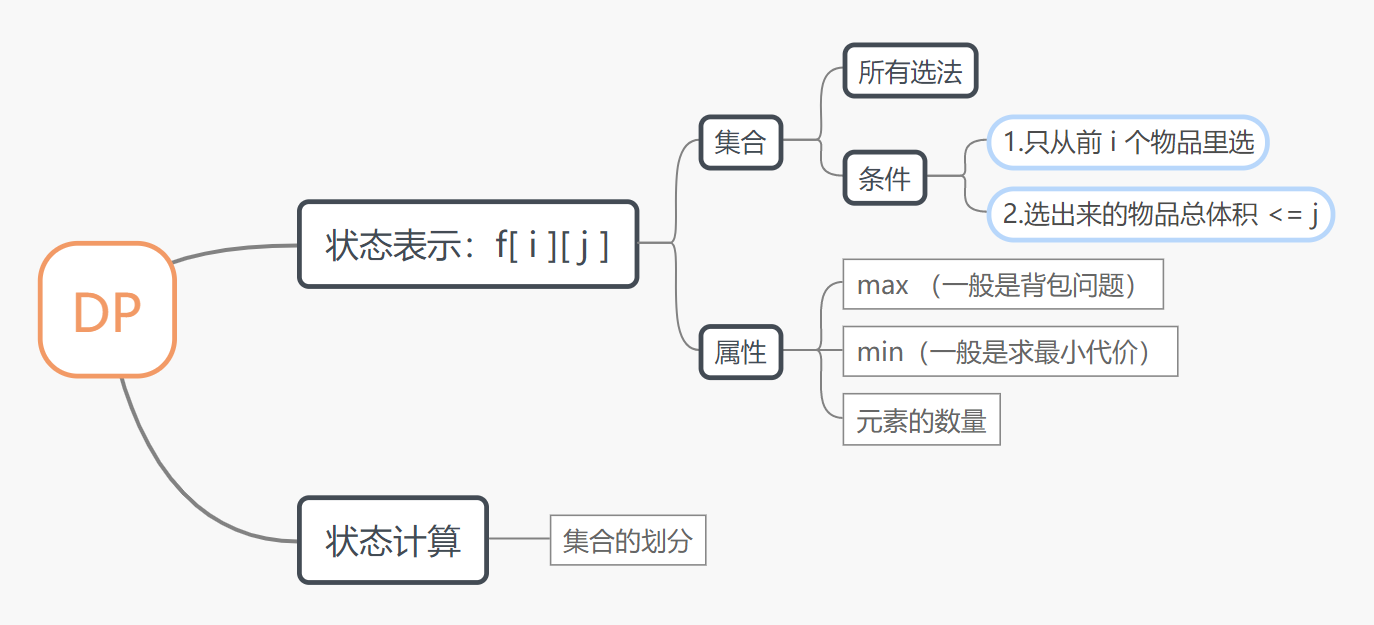
f[i][j]: 表示从前 i 个物品里选体积不超过 j 的最优解

这里分两种情况：
1. 当前背包容量不够（j < w[i]），前i-1个物品就是最优解：即f[i][j] = f[i - 1][j]
2. 当前背包容量够，判断选与不选第i个物品：

• 选：f[i][j] = f[i - 1][j - v[i]] + w[i]
  （把第i个删掉，求出前一个的最优解即f[i - 1][j - v[i]]，再加上第i个的价值 $ w[i] $ ）
• 不选：f[i][j] = f[i - 1][j]

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N];  // 物品的体积
int w[N];  // 每个物品的价值
int f[N][N];  // f[i][j]：从前 i 个物品选， 总体积不超过j,总体积的最大值

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )  // 枚举到第i个物品
        for (int j = 1; j <= m; j ++ ) // 枚举背包容量
        {
            // 如果放入第i个物品超重了，那就只能放到 i - 1 个 
            if(j < v[i])
                f[i][j] = f[i - 1][j];
            // 如果放入第i个物品没超重，就要决定放不放进去
            else 
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }

    cout << f[n][m] << endl;
    return 0;
}

优化成一维做法

其实我没懂，我是憨憨555

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = m; j >= v[i]; j -- )
        {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }

    cout << f[m] << endl;

    return 0;
}