题目描述:给定 n 个 0 和 n 个 1,它们将按照某种顺序排成长度为 2n 的序列,求它们能排列成的所有序列中,能够满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个。答案对 109+7 取模。
数据范围:1≤n≤105
组合计数,卡特兰数
解法
将 01 序列置于坐标系中,起点定于原点。若 0 表示向右走,1 表示向上走,那么任何前缀中 0 的个数不少于 1 的个数就转化为,路径上的任意一点,横坐标大于等于纵坐标。题目所求即为这样的合法路径数量。
下图中,表示从 (0,0) 走到 (n,n) 的路径,在绿线及以下表示合法,若触碰红线即不合法。
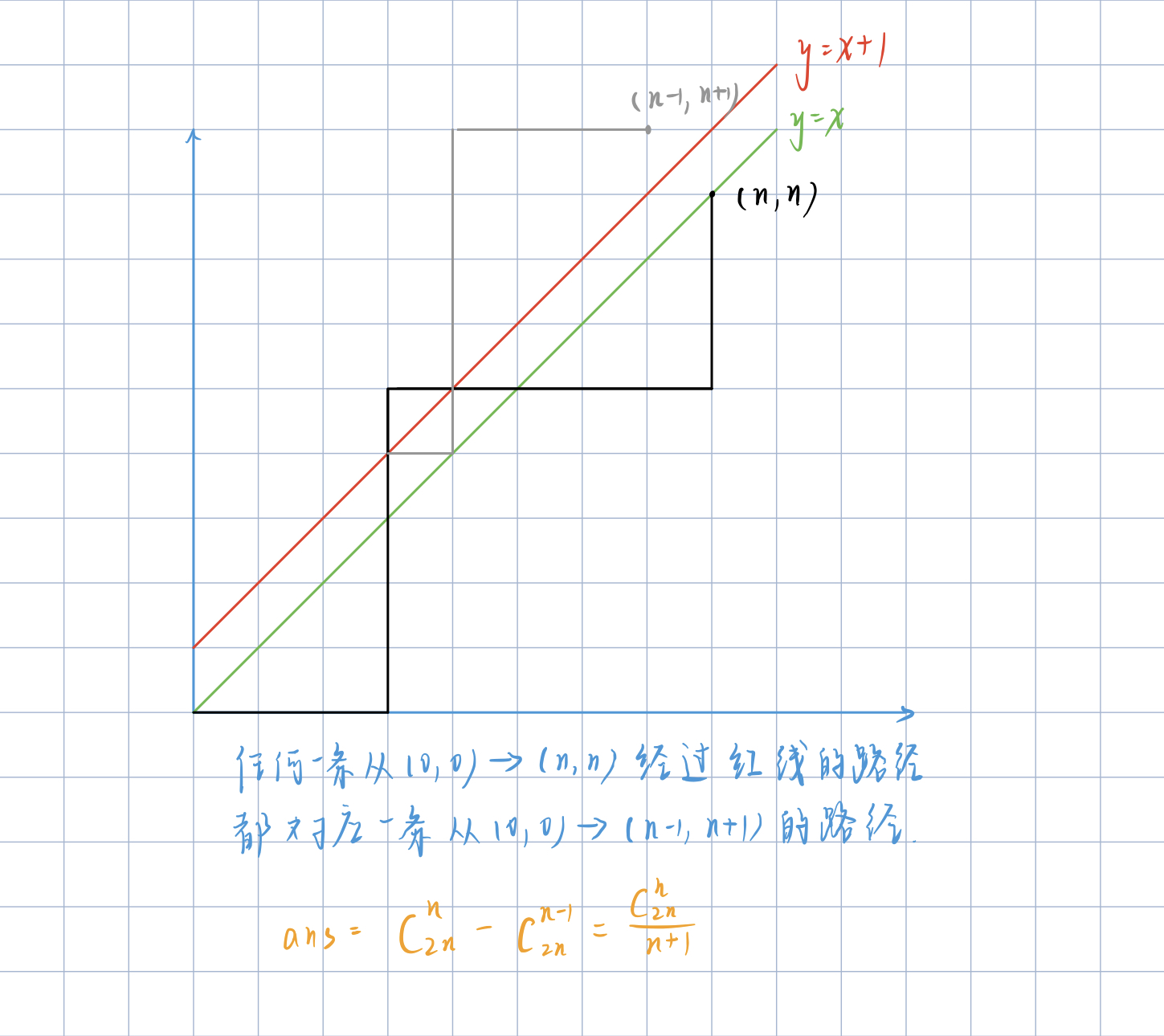
由图可知,任何一条不合法的路径(如黑色路径),都对应一条从 (0,0) 走到 (n−1,n+1) 的一条路径(如灰色路径)。而任何一条 (0,0) 走到 (n−1,n+1) 的路径,也对应了一条从 (0,0) 走到 (n,n) 的不合法路径。
答案如图,即卡特兰数。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 200010, mod = 1e9 + 7;
int n;
int fact[N], infact[N];
int ksm(int a, int k) {
int res = 1;
while (k) {
if (k & 1) res = (LL)res * a % mod;
a = (LL)a * a % mod;
k >>= 1;
}
return res;
}
void init() {
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i++) {
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * ksm(i, mod - 2) % mod;
}
}
int main() {
init();
cin >> n;
int res = (LL)fact[2 * n] * infact[n] % mod * infact[n] % mod * ksm(n + 1, mod - 2) % mod;
cout << res << endl;
return 0;
}


好图!偷了(会标注来源的
为什么除(n+1)也要用逆元来算qaq
只要\pmod p ,且p是质数,都必然是存在一个对应的逆元. 使得a * a^{-1) \equiv 1 \pmod p.
是只要mod了都要用逆元来算吗?直接除是不对的吗
根据我百度的模运算的运算法则,好像没有一个是除法,所以逆元的作用:保证计算过程中,每次计算符合模运算的规则.(模运算规则百度即可)
比如求\frac{a}{b}\pmod p,(p是质数).
\frac{a \bmod p}{b \bmod p} != 所求原式,因为没有除法的运算规则.但是如果我们找到一个x,使得
a \times x \equiv \frac{a}{b} \pmod p.
通过费马小定理可知,当模数p为质数,则
a^{p-1} \equiv 1 \pmod p
变换等式为 a \times a^{p-2} \equiv 1 \pmod p 显然,a^{p-2}就是所求逆元.
也就是说逆元的作用其实就是等量替代除法运算,变成乘法.
谢谢dalao。数论太难了qaq
是啊= =我觉得学算法就是学完后写博客,记录学习笔记= = 很多代码我都是跟着模仿的.写笔记的时候才顺便自己再写一遍…
太棒了吧这也
直接用
除法是对的,但是比起逆元所需要的乘法运算慢很多,为了追求效率所以求逆元不是吧,本来应该是能够整除的,但是为了避免写高精度,我们都是边算边模的。而在模意义下就不一定整除了,所以我们得找到一种能避免除法却又能满足整除性质的运算。
有道理,我一个月前写的我自己都蒙了
直接用除法不行的,乘上1 / 3和乘 3在模p意义下的逆元不是一个概念。
直接用除法不行的,乘上1 / 3和乘 3在模p意义下的逆元不是一个概念。
要是能严格证明就好了,光有个图,还是觉得有点那个了……
为啥不合法的路径数是C(n - 1) 2n呢?
即从 (0, 0) 走到 (n - 1, n + 1) 的所有方案数,一共要走 2n 步,其中向右走 n-1 步,向上走 n+1 步,组合数就是 C(2n, n - 1) 或者 C(2n, n + 1)
👍🏻 C(2n, n-1) == C(2n, n+1)
hh,ipad上的notability 配合 apple pencil 画的(其实就是只是画了几根直线而已呀)
知道了!感谢哦
主要字好看
这字也太好看了吧
orz
为什么最后必须ksm(n+1,mod-2) 前面已经预处理了,infact[n+1]怎么不行那?
ksm(n+1,mod-2) 是(n+1)的逆元,infact[n+1]是(n+1)!的逆元
emm这预处理逆元没有意义,增加了复杂度,但是题解写得好
是的,题目只有一组数据
懂了!解释的很清楚啊!
我指的那个卡特兰数
好偷,图了!
这么预处理有点浪费时间吧, 直接求逆元就行了.
不是,是因为分母是阶乘,我们需要计算阶乘的逆元,你能一个一个乘
如何用欧几里得算法求逆元呢
y总前面有视频
卧槽,这方法强的一
大佬 为什么
LL mz=fact[b]%p*infact[a-b]%p*infact[b]%p; LL nmz=fact[b-1]%p*infact[a-b+1]%p*infact[b-1]%p; LL res=mz-nmz%p;按原来的公式写会不对呢??
你把mz和nmz,都加上mod ,再%mod,最后的res写成res=(mz-nmz+mod)%mod,应该就对了
int res = (LL)fact[2 * n] * infact[n] % mod * infact[n] % mod * ksm(n + 1, mod - 2) % mod;大佬,这里的为什么要强制转化成long long 如果不转会怎么样
因为两个int相乘可能会爆int,所以先强制转化成long long了比较保险
那个我强制转化的是fact[2*n]还是这整个式子
只是fact[2 * n],这样他就是LL的,然后LL和后面的int相乘,int自动会转化为LL
好的,明白了
请问你画图的工具是什么呀,很漂亮~
Notability