提示

在我的 洛谷博客 中获得更好的阅读体验（图片显示问题）

前言

果然是$AcWing$中的困难难度题，花了我2个小时的时间才做出来，期间也看过另一篇题解，与我一开始的思路吻合，于是尝试了一下，花了一个小时，码了好几$KB$，第一次错了，发现有很大问题，于是推翻又码了好几$KB$,又发现了错误，然后感觉我的思路从根本上是有问题的，于是就放弃了这个思路，开始找规律......（此处省略无数次的失败提交和辛酸经历），终于解决了这道题，简直令我感动到眼泪流下来。

题目描述

题意还是挺明确的，至少我没有感觉到歧义，所以大略地讲一下：

在一个平面上有一个箱子，箱子有竖立，平行于x轴或平行于y轴几种可能，可以选择上下左右移动，然后同时箱子的位置会改变，状态可能会改变，给出起点和终点，要你求最少的步数。

算法1

宽搜 接近$O(xy)$

从起点开始宽搜，然后开一个$f[ch,i,j]$数组记录在ch状态下($U$,$V$,$H$)到达坐标$(x,y)$的最小步数，初始赋值为无限大，在宽搜过程中发现比原有答案小就入队，反复迭代优化，但基本上不会多次迭代（当然也有例外，要不然$SPFA$就不会死了），但面对如此大的数据范围，这种算法时间和空间肯定是都会超出限制的，但可以用来对拍，找规律（此题正解之一），所以也是很重要的。（多亏我先打了这个代码）

时间&空间复杂度

接近$O(xy)$

Pascal 代码

const max=100;min=-100;//定宽搜上线
var
  f:array['A'..'Z',-200..200,-200..200] of longint;
  a:array[0..10000000] of char;
  b,x,y:array[0..10000000] of longint;
  ch1,ch:char;  xx,yy,xxx,yyy,i,l,r:longint;
begin
  readln(ch1,xx,yy);
  fillchar(f,sizeof(f),63);//初始赋一个极大值，类似于memset
  l:=1; r:=1; a[1]:=ch1; b[1]:=0; x[1]:=xx; y[1]:=yy;
  f[ch1,xx,yy]:=0;//初始化宽搜队列，头尾指针和起点步数
  while l<=r do
  begin
    for i:=1 to 4 do//分别对应上下左右四个方向
    begin
      xxx:=x[l];
      yyy:=y[l];
      case i of
      1:case a[l] of
      'U':begin ch:='H'; yyy:=yyy+1; end;//注意箱子状态的变化，一定要仔细，别写错了，可以拿我的对照一下
      'H':begin ch:='U'; yyy:=yyy+2; end;//注意我们定位的方格在箱子中的位置，有时需要+或-2，后面也是一样的
      'V':begin ch:='V'; yyy:=yyy+1; end;
      end;//向上
      2:case a[l] of
      'U':begin ch:='H'; yyy:=yyy-2; end;
      'H':begin ch:='U'; yyy:=yyy-1; end;
      'V':begin ch:='V'; yyy:=yyy-1; end;
      end;//向下
      3:case a[l] of
      'H':begin ch:='H'; xxx:=xxx-1; end;
      'V':begin ch:='U'; xxx:=xxx-1; end;
      'U':begin ch:='V'; xxx:=xxx-2; end;
      end;//向左
      4:case a[l] of
      'H':begin ch:='H'; xxx:=xxx+1; end;
      'V':begin ch:='U'; xxx:=xxx+2; end;
      'U':begin ch:='V'; xxx:=xxx+1; end;
      end;//向右
      end;
      if (xxx>=min) and (yyy>=min) and (xxx<=max) and (yyy<=max) then//如果没有超出上限
      begin
        if b[l]+1<f[ch,xxx,yyy] then//并且答案更优
        begin
          f[ch,xxx,yyy]:=b[l]+1;
          inc(r);
          a[r]:=ch;
          b[r]:=b[l]+1;
          x[r]:=xxx;
          y[r]:=yyy;//更新答案+入宽搜队列
        end;
      end;
    end;
    inc(l);
  end;
  write(f['U',0,0]:3);//输出答案，带3个场宽，后面打表找规律时表格更整齐，规律可以好找不少
end.

麻烦诸位$C++$巨佬不要吐槽，我才刚来$AcWing$，我会把注释写的尽量明白的（虽然不写也看得懂）

算法2

(找规律/数学) $O(1)$

我想到的第二个思路，本来抱着试试看的心态，结果成为了我$A$掉这道题的方法
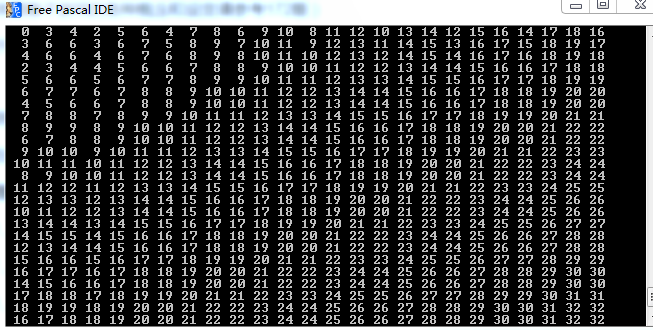
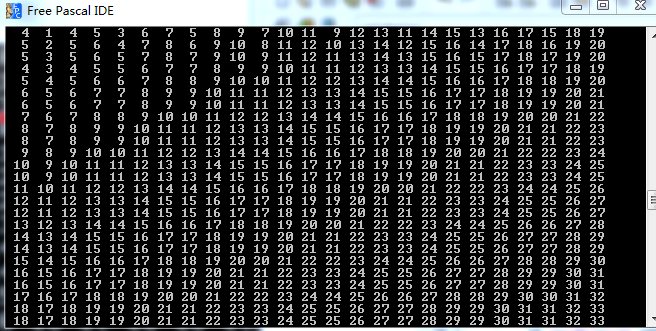
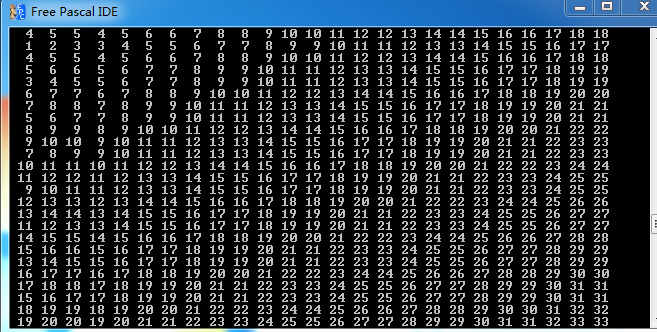
我们用之前贴出的代码在小数据中找一下规律，如下面三张图片
箱子状态为U 坐标x为0~24 y为0~24的答案

箱子状态为H 坐标x为0~24 y为0~24的答案

箱子状态为V 坐标x为0~24 y为0~24的答案

感觉好像有规律的样子，让我们先来分析为U情况下的规律

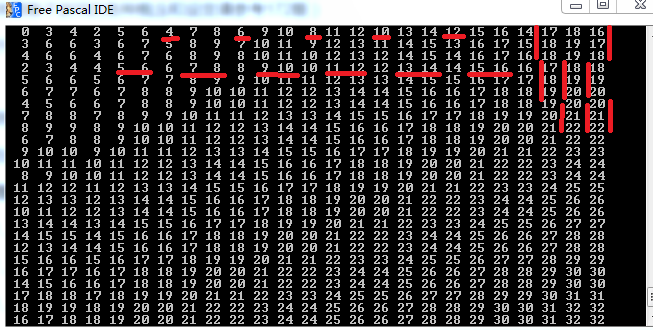
红线竖向标出，每三位一节连续自然数，但是从横向红线可以看出，只有在横向三位一节每节的最后一列，这样的循环是从第一个开始的，其他的都是从第4个开始的，同时最上面一行的数也有很明显规律，同样3位一节去寻找，这里就不列举具体公式了，可以自己推，也可以看我的代码

你以为这样就结束了......又不然我也不会这么心累了

仔细一看就会发现，前三列和前三行都不满足刚刚我们找出来的规律，所以对于前三行和前三列还要自己分别推出公式（当然也是有技巧的），无非就是三位一节分好之后找等差数列即可

当箱子状态为$H$或$V$的状态同理，但这两个之间是有规律的，可以从上面的图里看出来，行列反一下的答案是一样的(比如$H(1,3)=V(1,3)$)，所以只要找出其中一种状态的公式就可以了。

同时，我们还可以发现所得答案正负是对称的(如$U(1,1)=U(-1,1)$)，这也是很重要的一个规律

时间&空间复杂度

都是$O(1)$

C++ 代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll x,y,ans;
char ch;
int ansssu(int x,int y)//U状态的情况
{
    int ans;
    if (x<0) x=-x;
    if (y<0) y=-y;//负数取绝对值不影响结果
    if (x==0)
    {
        if (y%3==0) return y/3*2;
        else return y/3*2+2+y%3;
    }
    if (x==1)
    {
        if (y==0||y==3) return 3;
        if (y==1||y==2||y==4) return 6;//前面的好像没有规律，就打一个小表
        if (y%3==0) return y/3*2+1;
        else return y/3*2+3+y%3;//公式看不懂可以发帖询问，或者私信我，但最好还是自己推一下
    }
    if (x==2)
    {
        if (y==0||y==3) return 4;
        if (y==1||y==2||y==4) return 6;
        if (y%3==0) return y/3*2+2;
        else return y/3*2+3+y%3;
    }//分别判断x=0,1,2的情况
    if (x%3==0) return y/3*2+x/3*2+y%3;
    ans=(1+x/3)*2+x%3;
    if (y==0) return ans;
    else if (y==1||y==2) return ans+1;
    else return (y-3)/3*2+y%3+ans;//通用公式
}
int ansssh(int x,int y)//H状态的情况（用V也是可以的），于U的情况基本同理，就不注释了，但x,y必须分清
{
    int ans;
    if (x<0) x=-x;
    if (y<0) y=-y;
    if (x>=3&&y>=3) 
    {
        ans=y/3;
        ans=ans*2+3;
        if (y%3==2) ans++;
        return (x/3-1)*2+ans+x%3;
    }
    if (y==0||y==2)
    {
        if (x==0) return 4;
        if (x==1||x==2) return 5;
        return x/3*2+2+x%3;
    }
    if (y==1)
    {
        return x/3*2+1+x%3;
    }
    if (x==0)
    {
        ans=(y+1)/3*2+2;
        if (y%3==1) return ans-3;
        if (y%3==2) return ans;
        ans=y/3*2+3;
        return ans;
    }
    if (x==1)
    {
        ans=y/3*2+4;
        if (y%3==0) return ans;
        if (y%3==1) return ans-2;
        return ans+1;
    }
    if (x==2)
    {
        ans=y/3*2+4;
        if (y%3==0) return ans;
        if (y%3==1) return ans-1;
        return ans+1;
    }
}
int main()
{
    while (cin>>ch>>x>>y)
    {
        ans=0;
        if (ch=='U')
        {
           cout<<ansssu(x,y)<<endl;
        }
        if (ch=='H')
        {
            cout<<ansssh(x,y)<<endl;
        }
        if (ch=='V')
        {
            cout<<ansssh(y,x)<<endl;//找到相反这一个规律就可以少打不少内容
        }
    }
}

后记

这道题代码难度不大，主要侧重于思维，数学功底一定要扎实，这样可以更加轻松，而且一定要注意细节，思路要清楚，避免不必要的调试。

$All$ $in$ $all$还是要继续努力，两小时一道题还是有点慢......