题目描述

给定一棵含有 N 个结点二叉树的根结点，树中每个结点都 node.val 枚硬币，总共有 N 枚硬币。

每一次移动中，我们可以选择两个相邻的结点，然后从一个结点移动一枚硬币到另一个结点。（移动可以从父亲到儿子，或者从儿子到父亲。）

返回移动次数，使得每个结点仅含有一枚硬币

样例

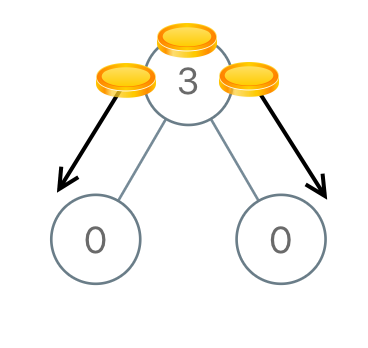
输入：[3,0,0]
输出：2
解释：从根结点开始，移动一枚硬币到左儿子，再移动一枚硬币到右儿子。

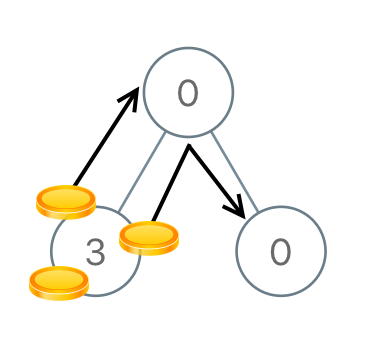
输入：[0,3,0]
输出：3
解释：从根结点的左儿子开始，我们移动两枚硬币到根结点【需要两次移动】。
然后，我们移动一枚硬币从根结点到它的右儿子上。

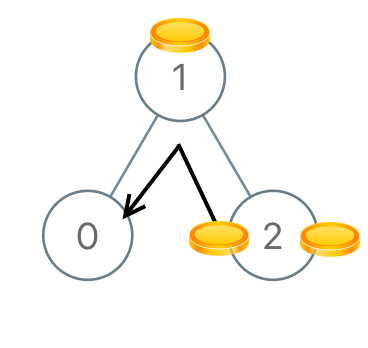
输入：[1,0,2]
输出：2

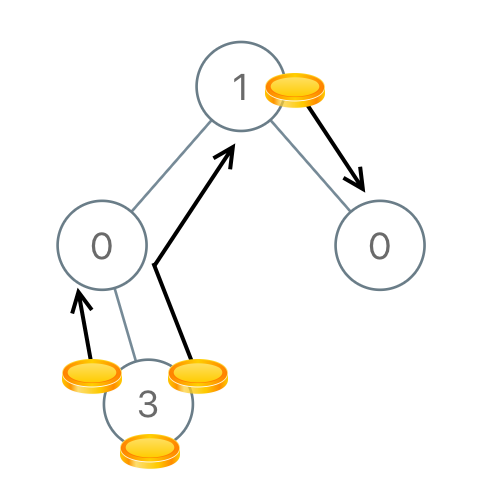
输入：[1,0,0,null,3]
输出：4

注意

• 1 <= N <= 100
• 0 <= node.val <= N

算法

(递归) $O(n)$

1. 我们自底向上的解决问题，假设每个结点的硬币数量可以为负数。首先我们满足叶子结点，使得叶子结点上的硬币数量都是 1，然后依次向上直到根结点。
2. 通过递归实现这个过程，在当前结点中，首先递归左右儿子，然后如果当前结点的硬币数量不足 1 个，则需要向父亲结点索要 1 - node.val 个；如果当前结点硬币数量大于 1 个，则向父亲结点送出 node.val - 1 个。索要和送出的个数需要累计到答案中。

时间复杂度

• 每个结点仅遍历一次，故时间复杂度为 $O(n)$。

空间

• 需要系统的栈空间来做递归，故空间复杂度为 $O(h)$，$h$ 为树的最大高度。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:

    void solve(TreeNode *rt, TreeNode *parent, int& ans) {
        if (rt == nullptr)
            return;
        solve(rt -> left, rt, ans);
        solve(rt -> right, rt, ans);

        if (rt -> val < 1) {
            parent -> val -= 1 - rt -> val;
            ans += 1 - rt -> val;
            rt -> val = 1;
        }
        else if (rt -> val > 1) {
            parent -> val += rt -> val - 1;
            ans += rt -> val - 1;
            rt -> val = 1;
        }
    }

    int distributeCoins(TreeNode* root) {
        int ans = 0;
        solve(root, nullptr, ans);
        return ans;
    }
};