题目描述

在一个NxN的棋盘上，有一个马被放在第r行第c列的位置，并且被移动K次。行和列的下标都是从0开始，所以左上角的方块下标是(0, 0), 右下角的下标是(N-1, N-1)。

马有8种可能的移动方式，如下图所示，每次移动在一个方向上移动1格，在另一个方向上移动2格。

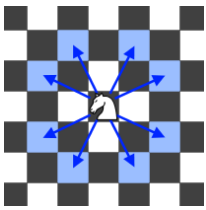
每次马移动的时候都随机从8种可能的移动方式中选一个，一直移动到马走出了棋盘或者移动次数到了K次以后停止。返回马停止移动后依旧在棋盘内的概率。

样例

输入: 3, 2, 0, 0
输出: 0.0625
说明: 第一次移动时有两种仍旧留在棋盘上的可能(移到(1, 2), (2, 1))，然后再从这两个位置继续移动，分别有2种可能依旧留在棋盘上，所以最后的概率为0.0625.

算法1

(深搜+数组记录) $O(k*N^2)$

考虑深搜，枚举移动的8个方向依次进行搜索，注意处理边界条件。为了避免重复搜索，用dp数组记录搜过的情况，之后就不用再次搜索了。

时间复杂度分析：$O(k*N^2)$

C++ 代码

class Solution {
public:
    int direction[8][2] = {{-1,2},{-1,-2},{1,2},{1,-2},{-2,1},{-2,-1},{2,1},{2,-1}};//8个方向
    double dp[26][26][105];//数组记录
    double help(int N,int r, int c, int K){
        if(r>=N||r<0)
            return 0;
        if(c>=N||c<0)
            return 0;
        if(dp[r][c][K]!=0)
            return dp[r][c][K];
        if(K==0)
            return 1;
        double res = 0;
        for(int i= 0;i<8;i++){
            res += 0.125*help(N,r+direction[i][0],c+direction[i][1],K-1);
        }
        dp[r][c][K] = res;
        return res;     
    }
    double knightProbability(int N, int K, int r, int c) {
        memset(dp,0,sizeof(dp));
        double res = help(N,r,c,K);
        return res;
    }
};