题目描述

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

样例

输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

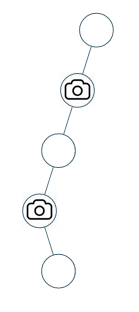
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

注意

• 给定树的节点数的范围是 [1, 1000]。
• 每个节点的值都是 0。

算法

(动态规划) $O(n)$

1. $f(i, 0)$ 表示 $i$ 结点被父结点监控的所需要的最少摄像头数量；同理，$f(i, 1)$ 和 $f(i, 2)$ 分别表示被自己监控和被某个儿子结点监控所需要的最少摄像头数量。
2. 我们通过递归的方式来更新 $f$ 数组；对于叶结点，$f(i, 0) = 0$，$f(i, 1) = 1$，$f(i, 2) = +\infty$。
3. 对非叶结点转移时，$f(i, 0)$ 不能取儿子结点中被父结点监控，所以很容易写出 $f(i, 0) = \min (f(j1, 1) + f(j2, 2)) + \min (f(j2, 1) + f(j2, 2))$；$f(i, 1)$ 可以取儿子结点中三种状态的最小值之和；$f(i, 2)$ 则需要某个儿子必须取“被自己监控”，其余取“被自己监控”和“被某个儿子监控”中的最小值。转移方程都可以很容易的写出。
4. 最终答案为，$\min (f(root, 1), f(root, 2))$。
5. 我们需要用一个哈希表，将指针映射到数字编号。

时间复杂度

• 每个结点仅遍历一次，遍历某个结点仅需要常数的时间更新，故总时间复杂度为 $O(n)$。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> f;
    int counter;
    unordered_map<TreeNode*, int> num;

    void solve(TreeNode *rt) {
        num[rt] = counter++;
        if (rt -> left == nullptr && rt -> right == nullptr) {
            f[num[rt]][0] = 0;
            f[num[rt]][1] = 1;
            f[num[rt]][2] = 1001;
        }

        else if (rt -> left != nullptr && rt -> right != nullptr) {
            solve(rt -> left);
            solve(rt -> right);

            f[num[rt]][0] = min(f[num[rt -> left]][1], f[num[rt -> left]][2])
                + min(f[num[rt -> right]][1], f[num[rt -> right]][2]);

            f[num[rt]][1] = 1
                + min(min(f[num[rt -> left]][0], f[num[rt -> left]][1]), f[num[rt -> left]][2])
                + min(min(f[num[rt -> right]][0], f[num[rt -> right]][1]), f[num[rt -> right]][2]);

            f[num[rt]][2] = min(
                f[num[rt -> left]][1] + min(f[num[rt -> right]][1], f[num[rt -> right]][2]),
                f[num[rt -> right]][1] + min(f[num[rt -> left]][1], f[num[rt -> left]][2])
            );
        }

        else if (rt -> left != nullptr && rt -> right == nullptr) {
            solve(rt -> left);

            f[num[rt]][0] = min(f[num[rt -> left]][1], f[num[rt -> left]][2]);

            f[num[rt]][1] = 1
                + min(min(f[num[rt -> left]][0], f[num[rt -> left]][1]), f[num[rt -> left]][2]);

            f[num[rt]][2] = f[num[rt -> left]][1];
        }

        else if (rt -> left == nullptr && rt -> right != nullptr) {
            solve(rt -> right);

            f[num[rt]][0] = min(f[num[rt -> right]][1], f[num[rt -> right]][2]);

            f[num[rt]][1] = 1
                + min(min(f[num[rt -> right]][0], f[num[rt -> right]][1]), f[num[rt -> right]][2]);

            f[num[rt]][2] = f[num[rt -> right]][1];
        }

    }

    int minCameraCover(TreeNode* root) {
        counter = 0;
        f = vector<vector<int>>(1000, vector<int>(3, 1001));
        solve(root);
        return min(f[num[root]][1], f[num[root]][2]);
    }
};