题目描述

给你一个 n 行 m 列的矩阵，最开始的时候，每个单元格中的值都是 0。

另有一个索引数组 indices，indices[i] = [ri, ci] 中的 ri 和 ci 分别表示指定的行和列（从 0 开始编号）。

你需要将每对 [ri, ci] 指定的行和列上的所有单元格的值加 1。

请你在执行完所有 indices 指定的增量操作后，返回矩阵中 奇数值单元格 的数目。

样例

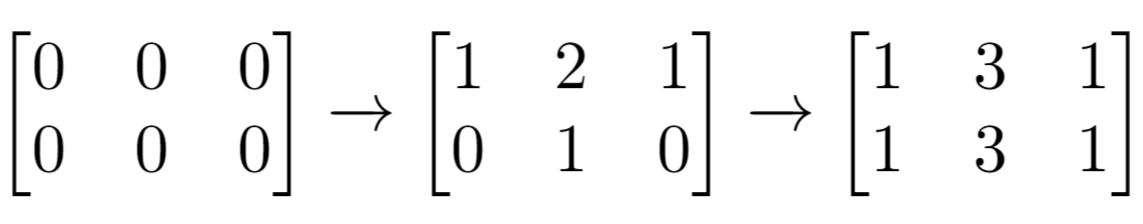
输入：n = 2, m = 3, indices = [[0,1],[1,1]]
输出：6
解释：最开始的矩阵是 [[0,0,0],[0,0,0]]。
第一次增量操作后得到 [[1,2,1],[0,1,0]]。
最后的矩阵是 [[1,3,1],[1,3,1]]，里面有 6 个奇数。

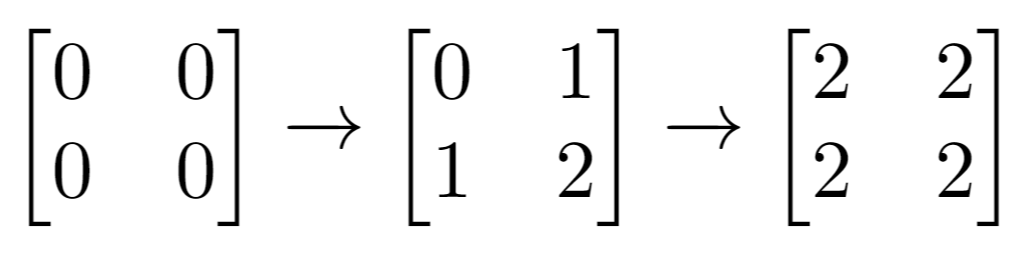
输入：n = 2, m = 2, indices = [[1,1],[0,0]]
输出：0
解释：最后的矩阵是 [[2,2],[2,2]]，里面没有奇数。

限制

• 1 <= n <= 50
• 1 <= m <= 50
• 1 <= indices.length <= 100
• 0 <= indices[i][0] < n
• 0 <= indices[i][1] < m

算法

(数学，哈希表) $O(L)$

1. 暴力的做法很简单，直接模拟即可。这里我们假设 n 和 m 都给到了 $10^9$，indices.length 即 L 给到了 $10^6$。
2. 分析哪些单元格最后会变成奇数。我们按行来看，假设这一行有过奇数次更新，则这一行中经过偶数次更新的列可以成为奇数；如果这一行经过偶数次更新，则这一行中经过奇数次更新的列可以成为奇数。
3. 我们如果统计出了有多少行经过了奇数次更新 cnt_r，以及有多少列经过了奇数次更新 cnt_c，则答案就是 cnt_r * (m - cnt_c) + cnt_c * (n - cnt_r)。
4. 统计以上信息可以用一个哈希表来记录。

时间复杂度

• 由于哈希表的时间复杂度是常数，我们只遍历一次 indices 数组即可完成统计。
• 故总时间复杂度为 $O(L)$。

空间复杂度

• 由于需要存储哈希表，而哈希表的大小与 $L$ 线性相关，故空间复杂度为 $O(L)$。

C++ 代码

class Solution {
public:
    int oddCells(int n, int m, vector<vector<int>>& indices) {
        unordered_map<int, int> r, c;
        int cnt_r = 0, cnt_c = 0;
        for (const auto &v : indices) {
            int &vr = r[v[0]], &vc = c[v[1]];
            vr ^= 1; vc ^= 1;
            cnt_r += (vr & 1) ? 1 : -1;
            cnt_c += (vc & 1) ? 1 : -1;
        }

        return cnt_r * (m - cnt_c) + cnt_c * (n - cnt_r);
    }
};