题目描述

将一个 二叉搜索树 就地转化为一个 已排序的双向循环链表 。

对于双向循环列表，你可以将左右孩子指针作为双向循环链表的前驱和后继指针，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

特别地，我们希望可以 就地 完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中最小元素的指针。

样例

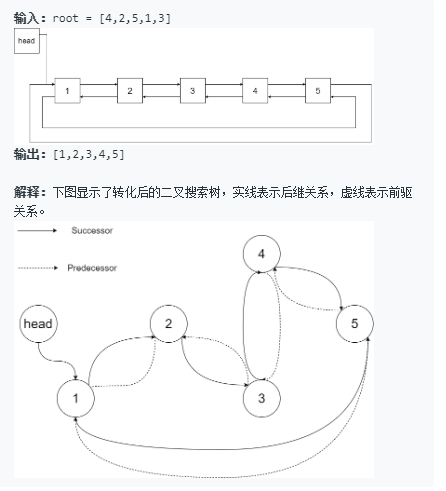
算法思路： 中序遍历

假设有这样的一个二叉搜索树：

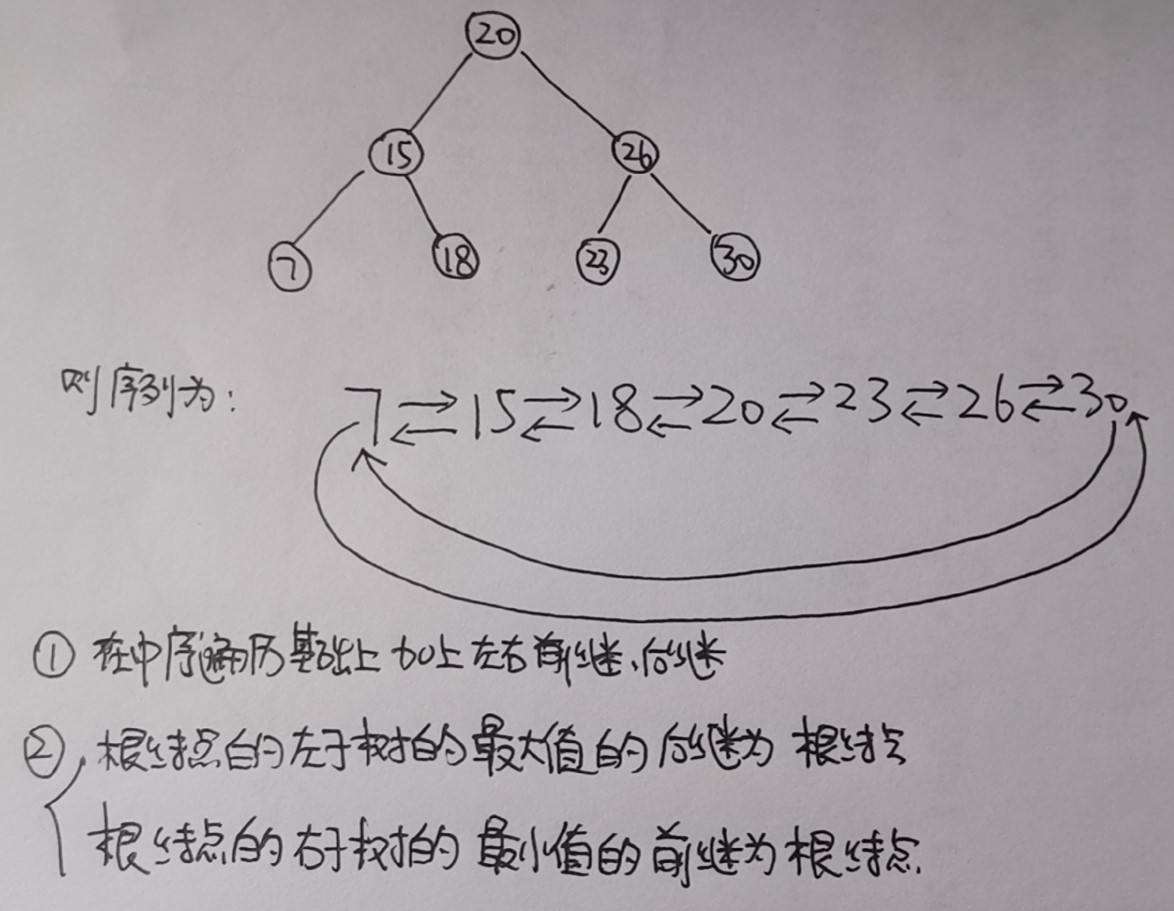
时间复杂度 $O(n)$

c++代码

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;

    Node() {}

    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }

    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/

class Solution {
public:
    //中序遍历O(n)
    pair<Node*, Node*> dfs(Node* root) //找到root为根的最小值和最大值节点
    {
        if(!root) return {NULL, NULL};
        auto left = dfs(root->left); //返回左子树的最小值和最大值
        auto right = dfs(root->right); //返回右子树的最小值和最大值

        //然后将左子树的最大值的后继 指向 根节点
        //    将右子树的最小值的前继 指向 根节点
        if(left.second){
            left.second -> right = root;
            root -> left = left.second;
        }
        if(right.first){
            right.first -> left = root;
            root -> right = right.first;
        }

        return {left.first? left.first : root, right.second? right.second : root};
    }

    Node* treeToDoublyList(Node* root) {
        if(!root) return NULL;
        auto p = dfs(root); //返回root为根的树的最小值和最大值节点

        p.first -> left = p.second;
        p.second -> right = p.first;
        return p.first;
    }
};