题目描述

城市的规划在城市建设中是个大问题。

不幸的是，很多城市在开始建设的时候并没有很好的规划，城市规模扩大之后规划不合理的问题就开始显现。

而这座名为 Fractal 的城市设想了这样的一个规划方案，如下图所示：

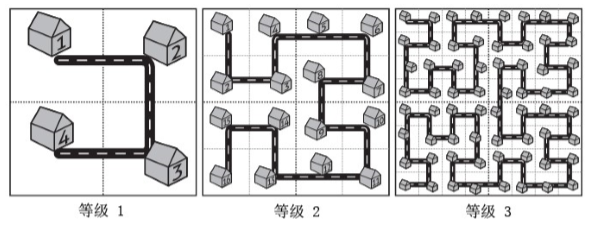
当城区规模扩大之后，Fractal 的解决方案是把和原来城区结构一样的区域按照图中的方式建设在城市周围，提升城市的等级。

对于任意等级的城市，我们把正方形街区从左上角开始按照道路标号。

虽然这个方案很烂，Fractal 规划部门的人员还是想知道，如果城市发展到了等级 N，编号为 A 和 B 的两个街区的直线距离是多少。

街区的距离指的是街区的中心点之间的距离，每个街区都是边长为 10 米的正方形。

输入格式
第一行输入正整数n，表示测试数据的数目。

以下n行，输入n组测试数据，每组一行。

每组数据包括三个整数 N,A,B, 表示城市等级以及两个街区的编号，整数之间用空格隔开。

输出格式
一共输出n行数据，每行对应一组测试数据的输出结果，结果四舍五入到整数。

数据范围
$ 1≤N≤31 $
$ 1≤A,B≤2^{2N} $
$ 1≤n≤1000 $
输入样例：

3 
1 1 2 
2 16 1 
3 4 33 

输出样例：

10 
30 
50 

递归+分治+数学坐标系公式+找规律

1. 递归+分治好理解，因为这个题目中最显著的特点就是，不断地重复旋转复制，也就是$N$级城市，可以由$4$个$N-1$级城市构造，因此我们每次可以不断地分形$N-1$级，将问题范围不断地缩小即可
2. 这道题目的数学坐标公式，其实一共有两个，一个是高中的数学函数，旋转，这是一个难点，其实可以通过找规律，求解，第二公式则是欧几里得距离公式。$ \sqrt{(x_1-x_2)^2 - (y_1-y_2)^2} $
3. 最难的就是如何旋转这个正方形 找规律。

总的来说这道题目数学知识较多，考察画图能力，解法自然，数据毒瘤，相信可以给你的NOIP一个有利的一脚。

1. 左上角：我们可以发现，左上角的$N-1$级矩阵其实就是等级为$N-1$，也就是上一个矩阵，顺时针旋转$90°$，那么既然如此的话，我们就可以综合yxc老师上课所讲的公式(补充:也就是旋转矩阵,属于大学的线性代数内容)，得出转移后的矩阵中的一点坐标从$(x,y)$变为$(y,x)$
2. 左下角：同左上角，它则是逆时针旋转$90°$而且还要水平翻转，也即是沿着$X$轴对称，原本逆时针后为$(y,-x)$，然后要对称,$x$坐标不变，$y$坐标取反，所以坐标为$(-y,-x)$ 也就是所谓的$(2 \times len-1 -y,len-1-x)$ 最难理解的坐标，具体可以画图理解
3. 右上角和右下角：通过$N=2$级图发现，其实和$N=1$是一样的，并没有旋转，只是平移，则右上角坐标为$(x,y+len)$，右下角坐标为$(x+len,y+len)$
4. 总的来说以上四种转移，都可以通过画图理解
5. 还有本题数据毒瘤，四舍五入最好是double类型，而且整数类型一定要是long long，否则容易WA！

易错点：公式使用，double型浮点数精度问题，输出格式化问题,还有@墨辛大佬指出的问题。

C++ 代码

以下为ACwingAc代码
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define PLL pair<ll,ll>
PLL calc(ll n,ll m)
{
    if (n==0)
        return make_pair(0,0);
    ll len=1LL<<(n-1),cnt=1LL<<(2*n-2);
    PLL pos=calc(n-1,m%cnt);
    ll x=pos.first,y=pos.second;
    ll z=m/cnt;
    if (z==0)
        return make_pair(y,x);
    if (z==1)
        return make_pair(x,y+len);
    if (z==2)
        return make_pair(x+len,y+len);
    return make_pair(2*len-1-y,len-1-x);
}
int main()
{
    //ios::sync_with_stdio(false);
    int t;
    cin>>t;
    while(t--)
    {
        ll n,a,b;
        cin>>n>>a>>b;
        PLL x=calc(n,a-1);
        PLL y=calc(n,b-1);
        ll dx=x.first-y.first,dy=x.second-y.second;
        double ans=(sqrt(dx*dx+dy*dy)*10);
        printf("%0.lf\n",ans);
    }
    return 0;
}

//以下为POJ&Acwing Ac代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
#define ll long long
#define PLL pair<ll,ll>
PLL calc(ll n,ll m)
{
    if (n==0)
        return make_pair(0,0);
    ll len=1LL<<(n-1),cnt=1LL<<(2*n-2);
    PLL pos=calc(n-1,m%cnt);
    ll x=pos.first,y=pos.second;
    ll z=m/cnt;
    if (z==0)
        return make_pair(y,x);
    if (z==1)
        return make_pair(x,y+len);
    if (z==2)
        return make_pair(x+len,y+len);
    return make_pair(2*len-1-y,len-1-x);
}
int main()
{
    //ios::sync_with_stdio(false);
    int t;
    scanf("%d",&t);
    while(t--)
    {
        ll n,a,b;
        scanf("%lld%lld%lld",&n,&a,&b);
        PLL x=calc(n,a-1);
        PLL y=calc(n,b-1);
        ll dx=x.first-y.first,dy=x.second-y.second;
        double ans=(sqrt(double(dx*dx+dy*dy))*10);
        printf("%0.lf\n",ans);
    }
    return 0;
}