于4.21修改了一个小错误

神仙题,不可做题.

12pts:就暴搜

36pts:考虑dp.
f[i][j]表示考虑到i,且最后一段是[j+1...i]的最小花费
S(i,j)表示[i..j]的和(显然可以预处理前缀和,然后O(1)计算)
转移方程:
$$f[i][j]=(\min_{0\le k<j,S(k+1,j)\le S(j+1,i)} f[j][k])+S(j+1,i)^2$$

64pts:
引理:设g[i]表示考虑到i的最小花费,last[i]表示最优决策下最后一段的和,则有:
$i$位置的最优决策,就是满足$last[j]\le S(j+1,i)$的最大$j$

感性的证明一下:首先,要证明这个最大合法$j$会让$g[i]$最小.
看这个图:

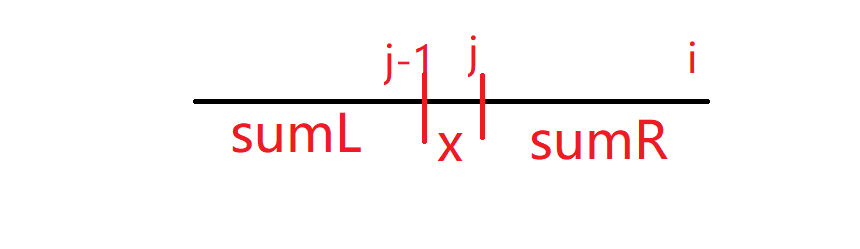
图中$j$表示最大合法$j$.选$j$的代价是:$(sumL+x)^2+sumR^2=sumL^2+x^2+2x\times sumL+sumR^2$
如果选择$j-1$,贡献是$sumL^2+(x+sumR)^2=sumL^2+x^2+2x\times sumR+sumR^2$
由于$j$合法,有$sumL+x\le sumR$.所以$sumL\le sumR$,那么$2x\times sumL\le 2x\times sumR$,选$j$更优.

其次,要证明选了这个之后不会让后面更劣.
$j$更大意味着更小的$last[j]$,那么后面的就可以分的更小更多,结果自然就更小了.
证毕.

那么,由引理,我们可以直接用$g[i]$来dp,找最大合法$j$就暴力枚举,时间复杂度$O(n^2)$,64pts.

88pts:
进一步优化.考虑一个$j$合法,当且仅当$S(j+1,i)\ge last[j]$,也就是$S(1,i)\ge S(1,j)+last[j]$
而$S(1,i)$是单调递增的,也就是说,合法的$j$的集合单调递增.

想到这里的时候,我直接用了变量维护法,但这样做是不对的.
因为$last[j]$没有单调性,所以合法的$j$出现不一定从$1$到$n$.用有点奇怪的单调队列优化.
队列维护的是一个$j$递增,$S(1,j)+last[j]$递增的集合(允许队列中存在不满足$S(1,i)\ge S(1,j)+last[j]$的$j$)
考虑处理队头:队头不一定是最优的,可能后面几个元素都是合法的.一种显而易见的解决方案是,只要第二个元素合法,就删除队头.但严格地说,队列不支持”访问第二个元素”.我们可以维护一个变量$maxv$表示当前的最优决策,只要队头合法就用它更新$maxv$并删除队头,最后$maxv$就是最优决策.
考虑处理队尾:如果存在不满足我们要求的$j$递增,$S(1,j)+last[j]$递增的单调性,也就是存在了
$$j1<j2,S(1,j1)+last[j1]\ge S(1,j2)+last[j2]$$
那么如果$j1$合法,$j2$一定合法,由引理,$j2$优于$j1$,所以$j1$不可能成为最优决策,直接从队尾删除.

这样求出$g[i]$后,再把$i$插入到队尾就好了.
时间复杂度$O(n)$

//省略快读
typedef long long ll;
ll n,type;
namespace type0
{
#define MAXN 500011
    ll f[MAXN],last[MAXN],a[MAXN],s[MAXN];
    ll q[MAXN],h,t;
    void solve()
    {
        for(ll i=1;i<=n;++i)a[i]=read(),s[i]=s[i-1]+a[i];
        f[0]=last[0]=0;
        h=t=1;
        q[t++]=0;//注意0也是合法的决策
        ll maxv=0;
        //si-sj\ge lastj
        for(ll i=1;i<=n;++i)
        {
            while(h<t&&s[q[h]]+last[q[h]]<=s[i])maxv=q[h++];
            last[i]=s[i]-s[maxv];
            f[i]=f[maxv]+last[i]*last[i];//这里的f就是g
            //printf("i=%lld:best=%lld,last=%lld,f=%lld\n",i,maxv,last[i],f[i]);
            while(h<t&&s[i]+last[i]<=s[q[t-1]]+last[q[t-1]])--t;
            q[t++]=i;
        }
        printf("%lld",f[n]);
    }

#undef MAXN

100pts:
需要高精度和卡空间.
然而用高精会TLE＆MLE．可以用两个long long代替高精,或者__int128(赛场上不能用)
但是空间还是很紧张.把b[],a[],s[]用同一个数组存,last[]和f[]不能开了,用nxt[i]表示到i的最优决策,最后倒推计算.
最终代码: https://www.acwing.com/activity/content/code/content/157664/