NIM游戏

定理：NIM博弈
A1 ^ A2 ^ … ^ An == 0 ——> 先手必败
A1 ^ A2 ^ … ^ An != 0 ——> 先手必胜

给定N堆物品，第i堆物品有Ai个。两名玩家轮流行动，每次可以任选一堆，取走任意多个物品，
可把一堆取光，但不能不取。取走最后一件物品者获胜。两人都采取最优策略，问先手是否必胜。

这种游戏称为NIM博弈。把游戏过程中面临的状态称为局面。
整局游戏第一个行动的称为先手，第二个行动的称为后手。
若在某一局面下无论采取何种行动，都会输掉游戏，则称该局面必败。

先手必胜状态：可以走到某一个必败状态
先手必败状态：走不到任何一个必败状态

最优策略是指，若在某一局面下存在某种行动，使得行动后使得对面进入先手必败状态，则优先采取该行动。

同时，这样的局面被称为必胜。我们讨论的博弈问题一般都只考虑理想情况，即两人均无失误，
都采取最优策略行动时游戏的结果。
NIM博弈不存在平局，只有先手必胜和先手必败两种情况。

SG函数

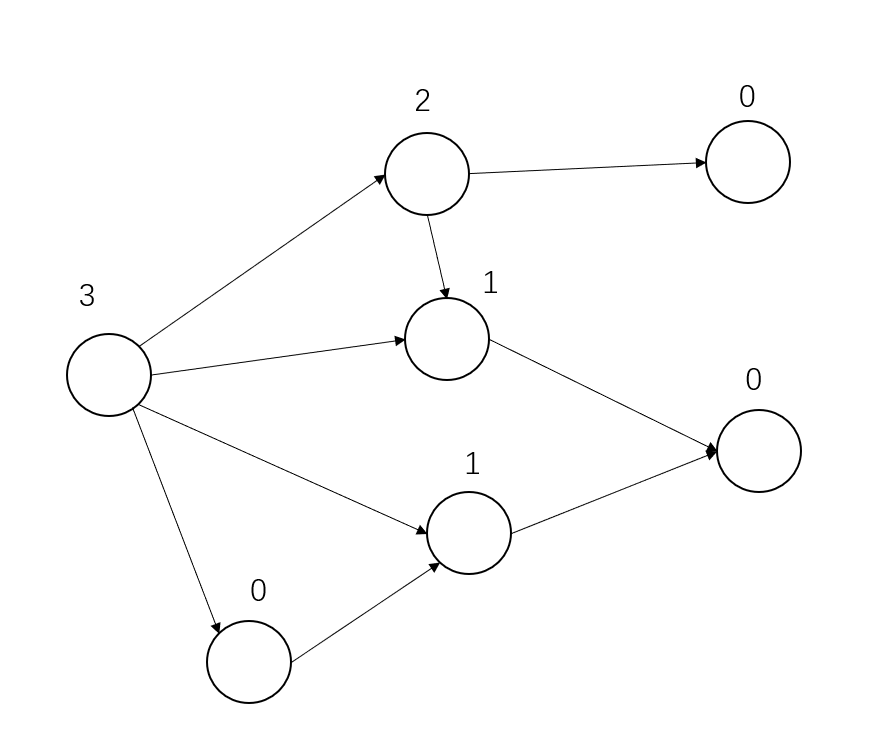
终点状态定义为0：
SG( 终点 ) = 0;

其他点状态定义为：
当前状态所不能到达的最小自然数

在有向图游戏中，对于每个节点x，设从x出发共有k条有向边，分别到达节点y1, y2, …, yk，
定义SG(x)为x的后继节点y1, y2, …, yk 的SG函数值构成的集合再执行mex(S)运算的结果，即：
SG(x) = mex( {SG(y1), SG(y2), …, SG(yk)} )

特别地，整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值，即SG(G) = SG(s)。

当
SG(x) == 0 ——> 必败（任何为0的状态不能走到终点，只能走到非零点）
SG(x) != 0 ——> 必胜

将n个图的局面异或每一个图的初始状态来进行判断

// 记忆化搜索
int sg(int x ) {
    //因为取石子数目的集合是已经确定了的,所以每个数的sg值也都是确定的,如果存储过了,直接返回即可
    if ( f[x] != -1 ) return f[x];

    unordered_set<int> S;
    for ( int i=0; i<m; i++ ) {
        int sum = s[i];
         //先延伸到终点的sg值后,再从后往前排查出所有数的sg值
        if ( x >= sum ) S.insert( sg(x-sum) );
    }
     //循环完之后可以进行选出最小的没有出现的自然数的操作
    for ( int i=0; ;i++ ) 
      if ( ! S.count(i) ) // 判断非空
         return f[x] = i;
}