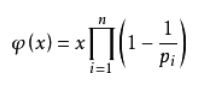
表示从1到n中所有与n互质的数的个数
注意pi与质因子的次数无关，只要有出现过都要乘
如：
6 = 2 * 3;
ϕ(6) = 6 * (1 - 1/2 ) * (1 - 1/3);
N = 2 ^ 100 * 3 ^ 100;
ϕ(N) = N * (1 - 1/2 ) * (1 - 1/3);

加上两个， 减去三个，加上四个…
原理：容斥原理

求欧拉函数

int phi(int n )
{
    int res = n;
    for (int i = 2; i <= n / i; i ++ )
        if (n % i == 0)
        {
            res = res / i * (i - 1); // i 等同 p， 表示约数
                 // res * ( 1 - 1 / i );
            while (n % i == 0) n /= i;
        }
    if (n > 1) res = res / n * (n - 1);

    return res;
}

筛法求欧拉函数

求 1 ~ N 中每一个数的欧拉函数

int primes[N], cnt;     // primes[]存储所有素数
int euler[N];           // 存储每个数的欧拉函数
bool st[N];         // st[x]存储x是否被筛掉


void get_eulers(int n)
{
    euler[1] = 1;
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i])
        {
            primes[cnt ++ ] = i;
            euler[i] = i - 1;  // 一个数x是质数，则1到x-1的数均与其互质
        }
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            int t = primes[j] * i;
            st[t] = true;
            /* 
            i % pj == 0:
             ϕ(i) 与 ϕ(pj *i) 的质因子相同
             ϕ(i) = i * ( 1 - 1/p1 ) * (1 - 1 / p2) *...(1 - 1 / pk) 
             ϕ(pj *i) = pj* i * ( 1 - 1/p1 ) * (1 - 1 / p2) *...(1 - 1 / pk) 
                      = pj * ϕ(i) 
             */
            if (i % primes[j] == 0)
            {
                euler[t] = euler[i] * primes[j];
            }
            /*
            i % pj != 0:
            ϕ(i) = i * ( 1 - 1/p1 ) * (1 - 1 / p2) *...(1 - 1 / pk) 
            ϕ(pj *i) = pj* i * ( 1 - 1/p1 ) * (1 - 1 / p2) *...(1 - 1 / pk) * (1 - 1 / pj)
                      = pj*ϕ(i)*(1 - 1 / pj) = ϕ(i)*( pj - 1)
            */
            else
            {
                euler[t] = euler[i] * (primes[j] - 1); 
            }

        }
    }
}

欧拉定理

若a与n互质，a^ϕ(n) ≡ 1 ( mod n ) ——> 同余

费马定理

若n为质数p，则有：
a^(p-1) ≡ 1 ( mod p )

快速幂

快速求解 a ^ k % p 的结果

先预处理出结果，再将k用二进制来表示，找到二进制中1的位置：

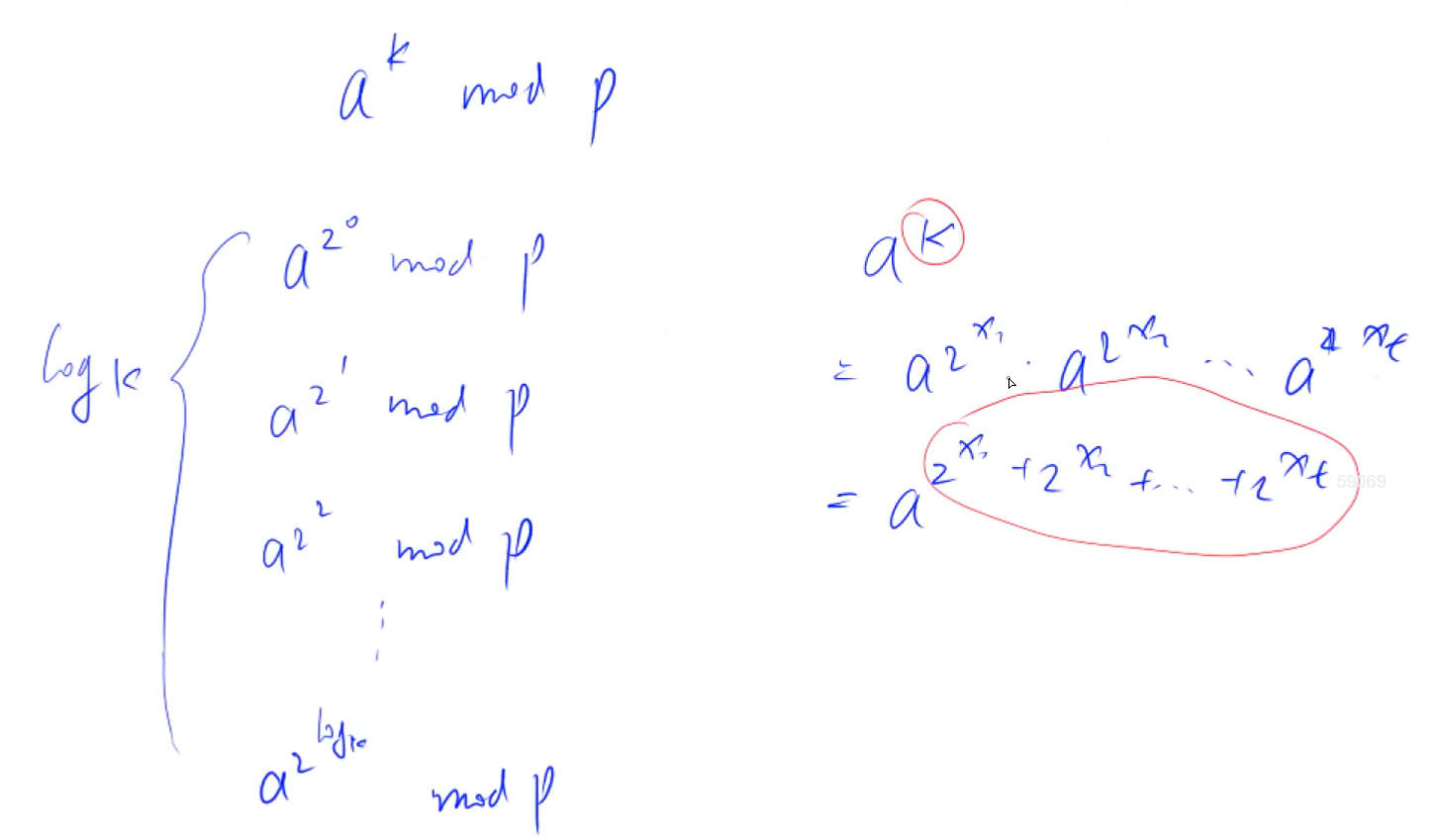
预处理：

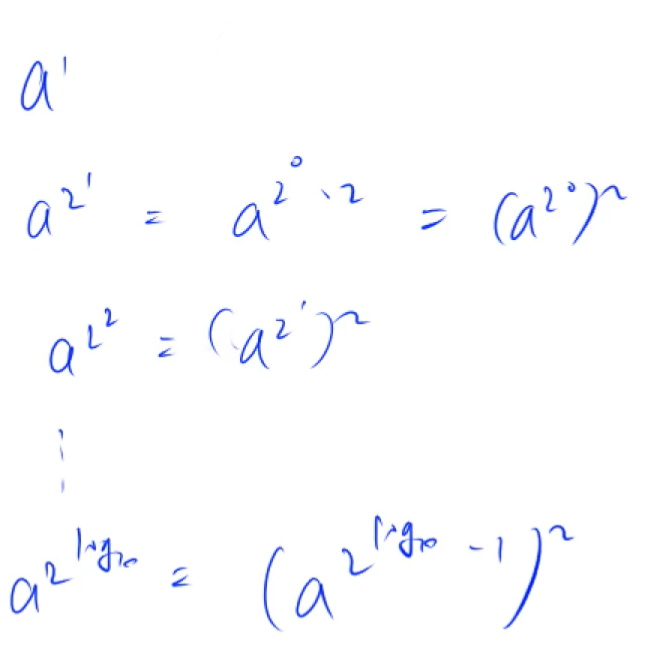
每一个数都是上一个数的平方再 % p

typedef long long LL;
LL qmi(int a, int k, int p)
{
    int res = 1 % p;
    while (k)
    {   
        // k末位是1
        if ( k & 1 ) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1; // k左移去掉当前位
    }
    return res;
}

快速幂求逆元

LL qmi( int a, int k, int p ) {
    int res = 1;
    // k使用二进制表示
    while ( k ) {
        if ( k & 1 ) res = ( LL ) res * a % p; // k最后一位是1
        k >>= 1; // 去掉最后一位
        a  = (LL) a * a % p;
    }
    return res;
}
// p为质数（费马小定理）
int res = qmi( a, p-2, p );