本笔记内容来源于算法基础课

最小生成树

1. Prim算法
   • 稠密图：朴素版Prim $O(n^2)$
   • 稀疏图：堆优化版Prim $O(m\lg n)$
2. Kruskal算法 $O(m\lg m)$

算法选择：

• 稠密图：朴素版Prim
• 稀疏图：Kruskal算法，相比于堆优化版Prim更简洁

通常为在无向图中求最小生成树，因此添加边注意添加正反两条

由于不最小生成树中不存在环，因此边权可以为负

对于重边：邻接矩阵维护最小权边，邻接表无需

朴素版Prim

点到集合的距离：点到集合中的所有点的路径中距离最短的的路径

思路：

距离初始化所有点到集合的距离 dist[i] = Inf
for (i : 0 ~ n - 1) 迭代n次
    t <- 找到集合外距离最近的点
    用 t 更新其他点到集合的距离
    st[t] = true

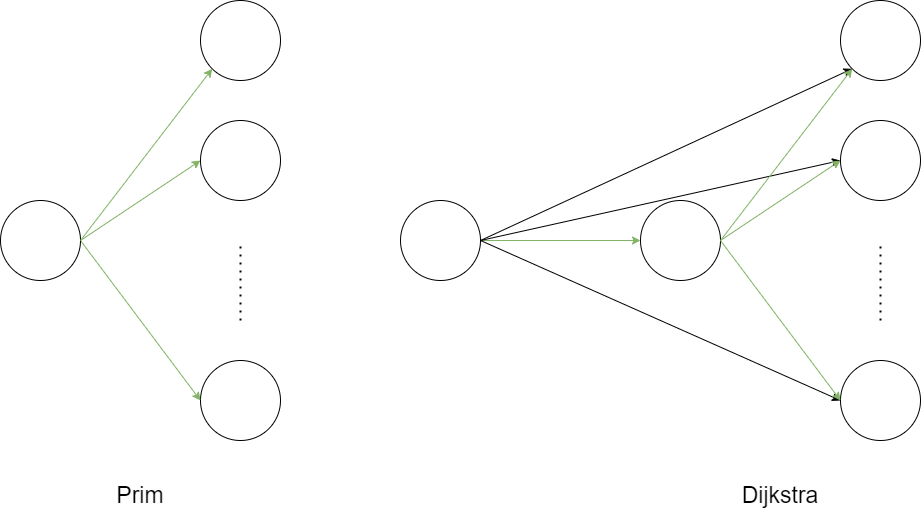
与Dij算法的区别在于距离的更新方式,Prim算法则是更新到集合的距离min(dist[j], g[t][j]),Dij算法中的距离是起始点到各个点的距离min(dist[j], dist[t] + g[t][j]

{:height=”80%” width=”80%”}

dist[N]点到集合的距离
st[N]是否加入到集合当中

int Prim() {
    for (int i = 1; i <= n; i++) dist[i] = Inf; // 距离初始化到集合的距离

    int res = 0; // 最小生成树边权和
    for (int i = 0; i < n; i++) { // 迭代n次
        int t = -1;
        for (int j = 1; j <= n; j++) { // 取出距离最小的点
            if (!st[j] && (t == -1 || dist[j] < dist[t]))
                t = j;
        }
        if (i != 0 && dist[t] == Inf) return Inf; // 当前图不连通
        if (i != 0) res += dist[t]; // 加入到权值
        for (int j = 1; j <= n; j++) 
            dist[j] = Integer.min(dist[j], g[t][j]); // 更新其他点到集合的距离
        st[t] = true;
    }
    return res;
}

注意需要先加入权重，再更新其他点到权重的距离，以防止加入的权重值错误

Kruskal算法

思路：

将所有边按权重从小到大排序 O(mlgm)
for 每条边 (a -> b, c) O(m)
    if a b 不连通
        将这条边加入到集合中

可以使用并查集来实现连通块的插入和查询

int Kruskal() {
    Arrays.sort(edges, 0, m, (o1, o2) -> o1.w - o2.w); // 从小到大排序所有边
    for (int i = 1; i <= n; i++) p[i] = i; // 初始化并查集
    int res = 0, cnt = 0; // res为边权和，cnt为加入的边的数目
    for (int i = 0; i < m; i++) {
        int a = edges[i].a;
        int b = edges[i].b;
        if (find(a) != find(b)){ // 判断是否属于同一个集合
            res += edges[i].w;
            cnt++;
            p[find(a)] = find(b); // 集合合并
        } 
    }
    if (cnt < n - 1) return Inf; // 没有加入n-1条边，说明不连通
    else return res;
}

二分图

判断一个图是否为二分图：
1. 染色法：$O(n + m)$
2. 匈牙利算法: $O(mn)$ 实际运行时间一般远小于$O(mn)$

染色法

一个图是二分图当前仅当这个图可以被二染色

一个图是二分图当且仅当图中不含奇数环

思路： dfs，尝试对所有节点涂色判断是否含有冲突

for (i : 1 ~ n)
    if i未染色
        dfs(i， 1) // 确定一个点则其可达的点的颜色都被确定

dfs(i, c): 
    染色c
    for 相邻所有点
        if 未染色
            染色~c
        else 
            判断染色是否冲突

dfs返回false说明染色时发生矛盾

int color[N]存储每个节点的颜色,0代表还未涂色，1,2代表两类节点

boolean dfs(int u, int c) {
    color[u] = c; // 当前节点涂色
    for (int i = h[u]; i != -1; i = ne[i]) { // 遍历周围节点
        int j = e[i];
        if (color[j] == 0) { // 如果未涂色，则尝试涂色
            if (!dfs(j, 3 - c)) return false; // 有矛盾则直接返回
        }
        else if (color[j] == c) return false; // 有涂色，则判断颜色是否相同冲突
    }
    return true; // 说明无冲突
}

因为考虑到图可能不连通，要对所有节点都尝试dfs

boolean flag = true;
for (int i = 1; i <= n; i++) {
    if (color[i] == 0) {
        flag = dfs(i, 1);
        if (!flag) break;
    }
}
if (flag) wr.write("Yes");
else wr.write("No");

匈牙利算法

求一个二分图的最大匹配

成功的匹配：不存在两条边共用一个点

思路：

对$a$尝试与$b$匹配一条边，如果$b$已经匹配，则对$b$尝试新的空闲匹配

考虑最坏情况，$b$需要尝试所有边，因此时间复杂度最坏为$O(mn)$

存左边指向右边的边集，因为需要遍历左边中点相邻的点

boolean st[N]标记点是否在匹配交换的过程，保证它不会再次重复区匹配交换已经标记的点，从而导致被无限尝试匹配交换
因此在对每个点匹配交换时，都需要清空st

int mathc[N]存储右边点所匹配的左边点

boolean find(int x) {
    for (int i = h[x]; i != -1; i = ne[i]) {
        int j = e[i];
        if (!st[j]) {
            st[j] = true;
            if (match[j] == 0 || find(match[j])) {
                match[j] = x; // 成功匹配
                return true;
            }
        }
    }
    return false;
}

对左边点依次寻找匹配,，注意每次清空标记数组st

int res = 0;
for (int i = 1; i <= n1; i++) {
    for (int j = 1; j <= n2; j++) st[j] = false;
    if (find(i)) res++;
}