CSAPP 第二章 信息的表示和处理

作者： 作者的头像   代码改变头发 ,  2021-08-17 16:17:37 ,  所有人可见 ,  阅读 526

2


CSAPP笔记&实验
本章属于第一部分:程序结构和执行. 包括 :

  • 信息存储 Information Storage

  • 整数表示 Integer Representations

  • 整数运算 Integer Arithmetic

  • 浮点数 Floating Point

对于拥有十个手指的人类而言, 使用十进制是很正常的. 但在构造存储和处理信息的处理器时, 二进制工作的更好:
二进制能够更容易的表示、存储和传输.(比如用高低电平表示0/1可以允许一定的偏差)

孤立而言, 单个的0/1位不是很有用. 然而把位组合 + 某种解释规则, 赋予不同可能的位模式以含义, 我们就能
表示任何有限集合的元素. (信息就是位 + 上下文)

我们将研究三种最重要的数字表示. 无符号(unsigned)表示大于等于0的数字; 补码(two's-complement)是
表示有符号整数的最常见方式; 浮点数(floating point)编码是表示实数的科学计数法的以2为基数的版本.
我们将会看到计算机在运算整数和浮点数运算过程中可能会出现意想不到的结果(反直觉的), 这是计算机用
有限的位表示无限数字所作的妥协(trade-off), 但重要的是计算可能没有产生期望的结果,但它是一致的!

2.1 信息存储

虚拟内存

通常情况下, 计算机以8bit/1byte作为最小的可寻址单元, 而不是访问单独的位bit.
程序将内存视为一个一维字节数组, 每个字节用唯一数字标识, 称为地址.
所有可能地址的集合称为虚拟内存地址(virtual adress space)
a.png

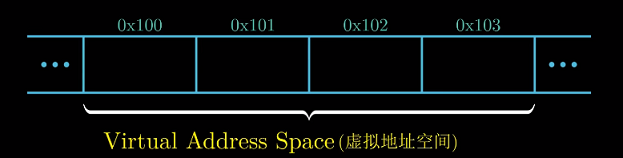
2.1.1 十六进制表示法
字节Byte :

8位组成, 每一位0/1. 在二进制表示法中, 它的值域是$00000000$~$11111111$.
如果看成十进制整数, 它的值域就是0~255.这种一位一位表示数据的方式称为位模式.
二进制表示太冗长, 十进制表示与位模式互相转换很麻烦. 所以我们用以16为基数, 或者
叫做16进制(hexadecimal)数来表示位模式.

16进制

简称Hex, 使用数字‘0’ ~ ‘9’和字符’A’ ~ ‘F’组成. 在C语言中以$0x$/$0X$开头的数字常量被认为是
16进制的值, 比如我们熟悉的$0x3f3f3f3f$. 大小写任意.

进制间转换

2进制/16进制 -> 10进制可以直接按位乘对应权重获得.
10进制-> k进制 可以用我们在树形DP用到的辗转相除法实现.

vector<int> convert(int x, int k)
{//十进制转为k进制
    vector<int> vec;
    while( x )  vec.push_back( x % k ), x /= k;
    reverse(vec.begin(), vec.end());
    return vec;
}

在C中输出整数的16进制表示可以用printf("%x")实现.

16进制->2进制 : 按位展开即可.
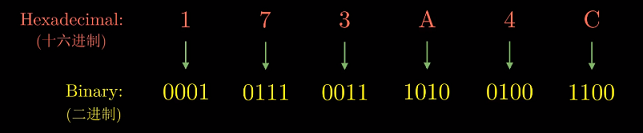
2-16.png
2进制->16进制 : 从右向左(低位到高位)按4位一组转换, 最后一组如果不到4位在前面补0.
1.png

2.png

$2^k$转为2进制 : 在1后面加$k$个0.
$2^k$转为16进制 : 2进制的4个0等价于16进制的1个0. $k = i+4j$, 那么16进制表示为$2^i$后面加$j$个0.

2.1.2 字数据大小 Word
字长

字是一个有点模糊的数据大小. 在计算机中字长决定的最重要系统参数是虚拟内存地址的最大大小. 对于
字长为$w$位的机器而言, 其虚拟地址范围为 $0$~$2^w-1$ , 程序最多访问$2^w$字节.

32位机到64位机的迁移

最近这些年出现了大规模的从32位字长机器到64位字长机器的迁移. 大多数64位机器也可以运行32位机器编译的
程序, 这是一种向后兼容 . 反之不能. 我们可以用不同的编译选项选择编译在32/64位机器运行的程序.

C中数据类型

C中不同数据类型在32/64位机器上所占字节 :
c.png
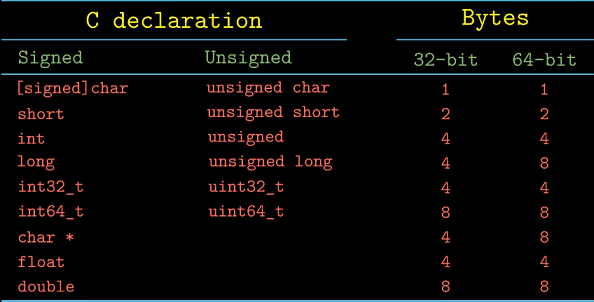
我们可以用sizeof运算符输出C中不同数据类型所占字节. 为了避免同一数据类型在不同机器上
字节大小可能变化, C中提供明确字节大小数据类型(如int32_t)

2.1.3 寻址和字节顺序
大小端

我们已经知道计算机是以byte为寻址单位, 对于跨越多个byte的程序对象, 必须建立两个规则

  • 程序对象的地址

  • 如何排列多个字节

几乎在所有机器上, 多字节对象都被存储为连续的字节序列, 地址为所使用字节的最小地址.
那么可以想到有两种排列顺序 : 从低地址到高地址, 可以从低位字节->高位字节, 或者顺序颠倒.
前一种规则称为小端法(little endian), 后一种称为大端法(big endian) . 以int类型的变量x
为例, 其16进制值为0x01234567, 位于地址0x100处(字节序列的最小地址)
端.png
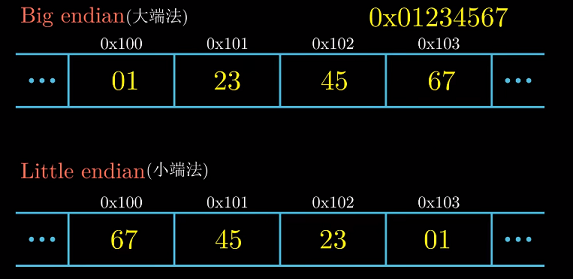
注意这里01为最高位字节.

只要选择其中一种规则并 始终如一地坚持 , 对于哪种字节排序都是任意的.

大小端何时可见

在大部分情况下(比如我们做算法题时)机器使用的字节顺序是完全不可见的, 不过有时字节顺序会成为问题.

  • 在不同类型的机器间通过网络传输二进制数据时. 网络应用程序的代码编写必须确保发送方机器
    将它内部的表示转换为网络标准, 而接收方机器将网络标转转换为它的内部表示.

  • 阅读表示整型数据的字节序列, 这常发生在阅读汇编代码时.

  • 在编写规避正常类型系统的程序时, 比如C中不同数据类型间的强制类型转换(cast)

字节打印代码
#include <stdio.h>

typedef unsigned char* byte_pointer; //字节指针(char 一个字节)

void show_bytes(byte_pointer start, size_t len)
{//按字节序打印一端字节序列的值(hex) start作为字节数组的首地址
    size_t i;
    for( i = 0; i < len; i++ )
        printf("%.2x ",start[i]);//%x 打印字节的地址
    printf("\n");
}

void show_int(int x)
{//类型转换:将int转为当作长度为4的字节序列
    show_bytes( (byte_pointer)&x, sizeof(int) );
}

void show_float(float x)
{
    show_bytes( (byte_pointer)&x, sizeof(float) );
}

void show_pointer(void *x)
{
    show_bytes( (byte_pointer)&x, sizeof(void *));
}

void test_show_bytes(int val)
{
    int ival = val;
    float fval = (float)val;
    int *pval = &val;
    printf("show_int : "); show_int( ival );
    printf("show_float: "); show_float( fval );
    printf("show_pointer : "); show_pointer( pval );
}

int main()
{
    int x = 12345; //0x00003039
    test_show_bytes(x);
}
/* 
 *show_int : 39 30 00 00 低字节39在低地址 --> 小端机器
 *show_float: 00 e4 40 46 
 *show_pointer : 8c 83 1c b3 ff 7f 00 00 
 */

代码关键部分为show_bytes函数, 将任意类型作为字节数组按地址顺序输出内容. 其中void*可以
保存任意数据类型的指针.

书中在4中机器上运行了上述代码.

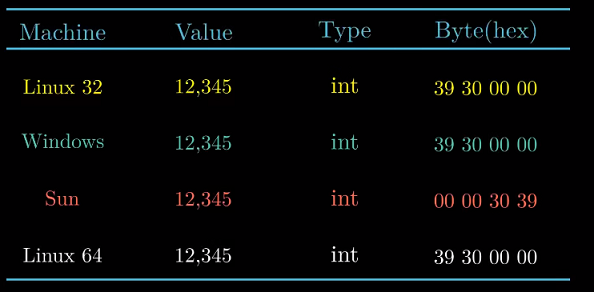
int.png

f.png

p.png

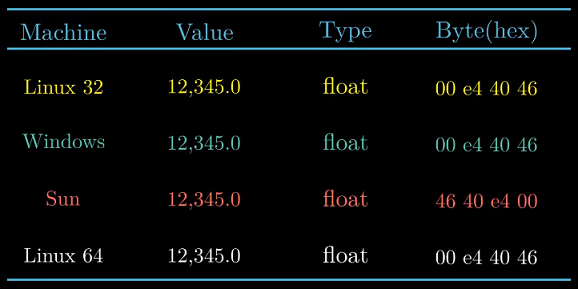
可以看出只有Sun机器是大端法机器. int和float数据除字节顺序均相同. 但不同机器/操作系统
使用不同存储分配机制, 所以地址均不相同.(同一机器不同时间运行同一代码可能地址也不相同)

int : 0x 39 30 00 00 ; float : 0x 00 e4 40 46. 观察它们的二进制表示 :
配.png
两种编码有13位的匹配. 这是否是个巧合呢 ?

2.1.4 表示字符串
字符串的平台独立性

C中字符串被编码为以null(assii值为0)的字符数组.
s.png
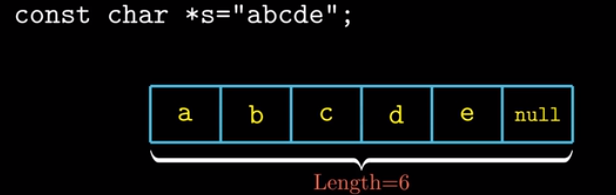
运行字节打印代码

int main()
{
    char *s = "12345";
    show_bytes( (byte_pointer)s, 6 );
}
/* 
 *31 32 33 34 35 00 
 */

最后的00即结尾的null.

使用ascii码表示字符在任何系统上都会得到相同结果, 与字节顺序和字的大小无关. 因而,
文本数据比二进制数据具有更强的平台独立性.

2.1.6 布尔代数简介
布尔代数 Boolean algebra

二进制值是计算机编码、存储和操作信息的核心. 所以围绕数值0和1的研究已经演化出了丰富的数学知识
体系. 这起源于1850年前后乔治·布尔(George Boole,1815-1894)的工作.

bool.png

2.1.7 C语言中的位级运算

C的一个特性就是支持对位向量按位进行布尔运算. 位向量 : 固定长度为w, 由0, 1组成的串.
bit.png
应用 :

  • 位向量表示有限集合. 比如状态压缩DP.
  • 位运算实现掩码操作 比如取整型数据x的低字节 x & 0xFF
2.1.8 C语言中的逻辑运算
逻辑运算特点
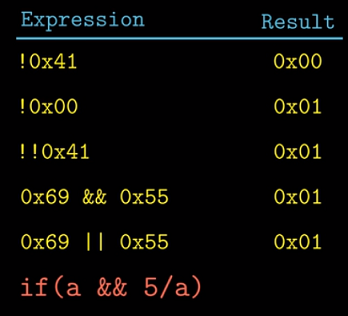
  • 仅有True/False : 逻辑运算认为所有非零参数表示True, 0表示Flase. 比如我们常见的if(!x)
  • 提前终止(短路) : 如果第一个参数值就能确定表达式结果, 那么逻辑运算停止运算. 比如
    if(a && 5/a)如果a为0, 运算返回False, 不会出现除以0的情况.
    逻辑.png
2.1.8 C语言中的移位运算
左移

x << y 位向量x向左移动y位, 丢弃高y位, 多出的低位用0填补.
例如00110左移三位 –> 10000

右移

  • 逻辑右移 与左移类似, x >> y, 丢弃低y位, 多出高位用0填补

  • 算数右移 有符号整数的最高位位符号位, 此时多出的高位用符号位填补.

移位.png

一般对无符号整数采用逻辑移位, 对有符号整数右移时采用算数右移.

对32位类型的int移位32会得到什么结果
int main()
{
    int a = 1;
    printf("a << 32 = %d\n", a << 32);
    printf("a << 33 = %d\n", a << 33);
    printf("a << 31 << 1 = %d\n",a << 31 << 1);
}
/*
 *a << 32 = 1
 *a << 33 = 2
 *a << 31 << 1 = 0
 */

对宽度为w的数据类型左移y位, 实际移位为$y mod w$ 位. 但最好保持移位量小于待移位数值的位数.

2.2 整数表示

本节中我们描述用位来编码整数的两种方式, 一种表示非负数, 另一种能够表示负数、零和正数. 我们
将会看到它们在数学属性和机器级实现方面的密切相关. 我们还会研究扩展或收缩一个已编码整数以
适应不同长度表示.

2.2.1 整数数据类型

C语言支持多种整型数据类型–表示有限范围的整数.

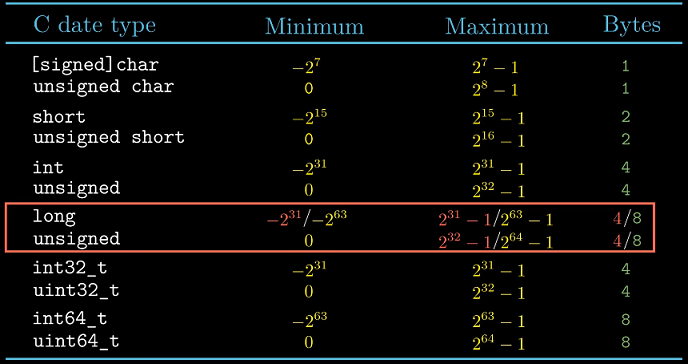
int.png

不同数据类型所占字节与值域都是不同的. 这里long是唯一一个与及其机器相关的, 其在32/64
位机器上占4/8字节. unsigned表示数字是非负的无符号整数.

2.2.2 无符号数的编码
$B2U_w$

假设位向量$x$有$w$位,$x_{w-1},…,x_0$. 用$B2U_w$(Binary to Unsigned)表示从位向量到整数的映射.

无向量.png

$B2U_4[0101]$ = $2^2 + 2^0 = 5$

图形化表示

我们把第i位权重用蓝色箭头表示.$x$的值即位为1对应箭头长度之和.
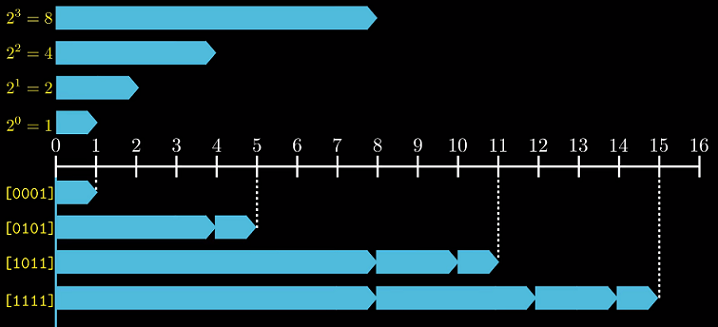
无图形.png

2.2.3 补码编码(有符号整数)

最常见的有符号数的计算机表示方法就是补码two's-complement形式. 这里将向量最高位解释为负权.
所以我们将最高位称为符号位(即使其他正权均为1,即11…11,其值仍为负数-1)

$B2T_w$

假设位向量$x$有$w$位,$x_{w-1},…,x_0$. 用$B2T_w$(Binary to Two’s-complement)表示从位向量到整数的映射.

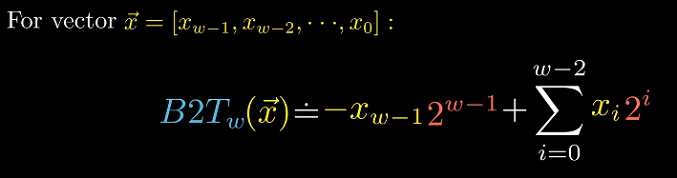
有向量.png

$B2T_4[1001]$ = $-1 * 2^3 + 1 * 2^0 = -7$

图形化表示

这里用向左指的箭头表示负数.
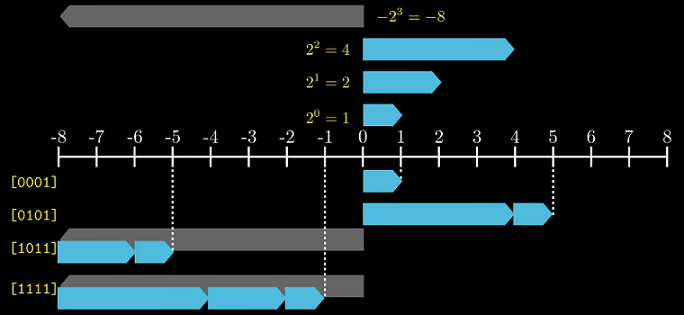
有图形.png

数值范围

无符号整数最大值
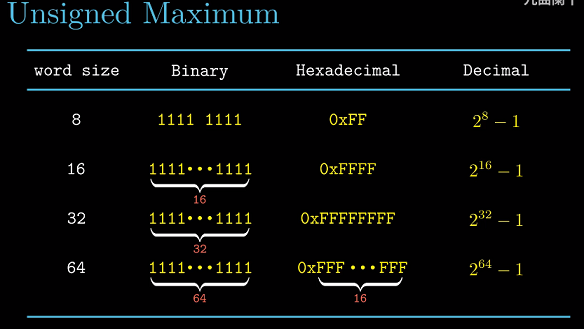
Umax.png
之后我们用$UMax_w$表示w位无符号整数的最大值, $UMax_w = 2^w - 1$

有符号整数最大值
TMax.png
之后我们用$TMax_w$表示w位有符号整数的最大值, $TMax_w = 2^{w-1}- 1$

有符号整数最小值
TMin.png
之后我们用$TMin_w$表示w位有符号整数的最小值, $TMin_w = -2^{w-1}$

-1的表示
-1.png
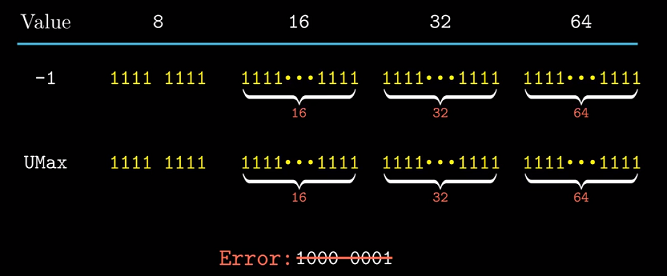
-1的二进制表示为全1, 恰好与$UMax$的二进制表示相同.

几个值得注意的数字关系
  • $|TMin|$ = $|TMax|+1$, 也就是说$TMin$没有与之对应的正数
  • $UMax$ = $2TMax + 1$

$TMin$的特殊性容易造成程序中细微的错误. 这种不对成性是由于非负数有一个表示为0.

int main()
{
    //limits.h中定义了几个常量以描述无符号数和有符号数的范围
    printf("abs(Tmin) = %d\n",abs(INT_MIN));
}
/*
 *abs(Tmin) = -2147483648
 */

C语言标准没有规定用补码形式表示有符号整数, 但几乎所有机器都是这么做的.

一个例子

为进一步理解补码, 考虑下面的代码

int main()
{
    short x = 12345, nx = -x;
    unsigned short unx = nx;
    show_short(x); show_short(nx); show_unsigned_short(nx);
}
/*
 *39 30 
 *c7 cf 
 *c7 cf 
 */

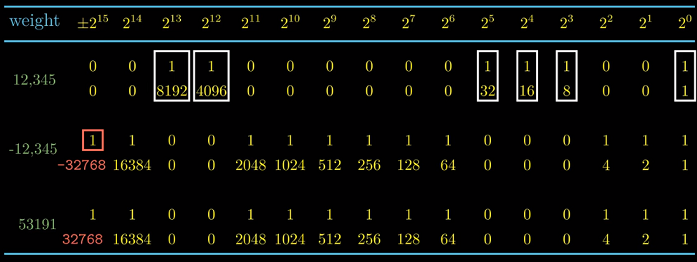
例子.png

从上面例子可以观察到x与-x的补码表示. 也可以观察到有符号转换为无符号后位模式不变, 只是
改变了解释规则.

2.2.4 有符号和无符号数字间的转换
位级别

C允许在各种不同的数字数据类型之间做强制类型转换.

int main()
{
    short int v = -12345;
    unsigned short uv = (unsigned short)v;
    printf("v = %d, uv = %u\n", v, uv);
    show_short(v); show_unsigned_short(uv);
}
/*
 *v = -12345, uv = 53191
 *c7 cf 
 *c7 cf 
 */

对于大多数C语言的实现, 有符号数和无符号数的转换在位级别是不变的, 只是解释规则改变.

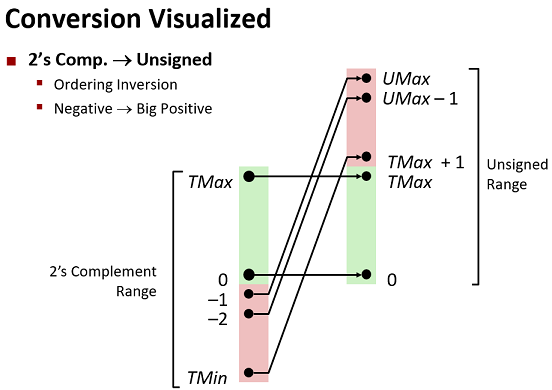
映射函数关系$B2U与B2T$

区别在最高位的权重值
函数关系.png

我们用T2U(x)表示从补码到无符号的转换. 在最高位为1时, 无符号和有符号相差
最高位权重的两倍即$2^w$.
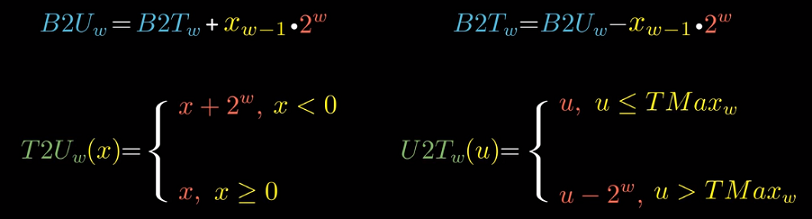
fun.png

数值关系
1.png

2.2.5 C语言中的有符号数和无符号数

C中大多数数字都默认为是有符号的, 创建一个无符号常量必须加上后缀’U’/’u’. 除了显式类型转换,
当一种类型的表达式赋值给另一种类型的变量时, 发生隐式类型转换.

当执行一个运算时, 如果运算数一个是有符号的另一个是无符号的, 那么C会隐式地将有符号参数
强制类型转换为无符号数. 有时这会导致非直观的结果甚至发生难以察觉的错误.

int main()
{
    int neg_one = -1; unsigned int zero = 0;
    if( zero < neg_one )
        puts("0U < -1!");

}
/*
 *0U < -1!
 */

有符号-1隐式转换为无符号数UMax!

不同字长整数间的转换
  • 将一个较小数据类型->较大, 扩展高位, 数值保持不变(没有信息遗漏)
  • 将一个较大数据类型->较小, 截断高位, 数值可能改变(遗漏部分信息)
2.2.6 扩展一个数字的位的表示
无符号数位扩展(零扩展 zero extension)

高位补0即可.
2.png
根据$B2U$可以知道零扩展后无符号整数数值不变.

有符号数位扩展(符号扩展 sign extension)

高位补符号位即最高位.
4.png

符号扩展证明 :
宽度为w的补码扩展k位, 证明$B2T_w(x_{w-1},…,x_0) = B2T_{w+k}(x_{w+k-1},…,x_{w-1},…,x_0)$

a.png

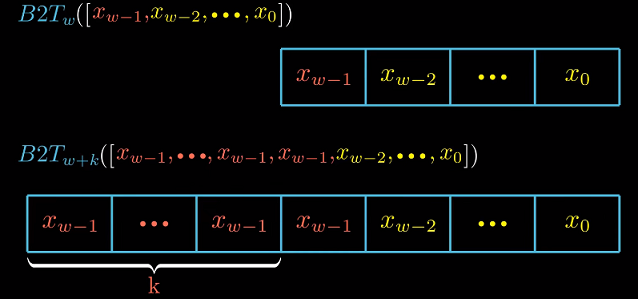
证明$B2T_w == B2T_{w+k}$, 根据归纳法我们只需证明对任意长度w, $B2T_w == B2T_{w+1}$即可.

b.png

我们把$B2T_w$ 和 $B2T_{w+k}$展开相减, 结果为0.
c.png

2.2.7 截断数字 truncate
规则

我们把较大的$W$位数字转换为较小的$w$位时, 只保留$W$位的低$w$位, 截断高$W-w$位.

截断无符号数

将$x$截断为$k$位, 相当于$x mod 2^k$. (高位权重都是$2^k$的倍数, 取模结果为0).
这里可以类比10进制, 如果我们想将10进制数字截断为3位, 对$10^3$取摸即可.

d.png

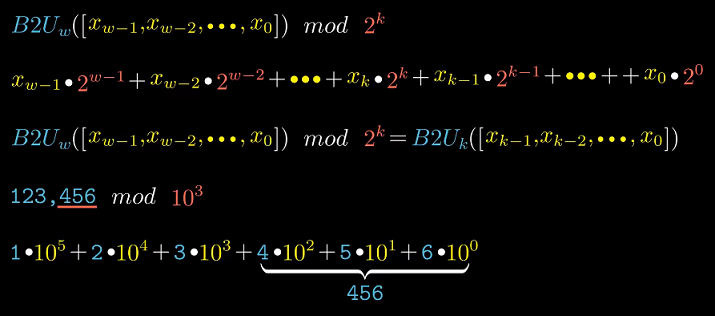
截断有符号数

书中给出比较长的公式解释如何截断有符号数, 实际上就是将$x$当作无符号数将高位截断, 再把截断后
的低k位结果当作有符号数解释.

e.png

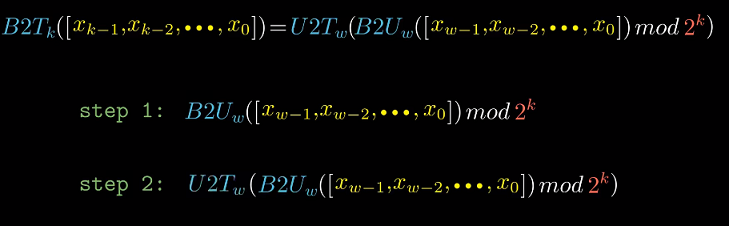
隐式转换错误例子

在有符号和无符号数转换的过程中可能会出现非直观的结果, 导致难以发现的错误.

ex1
#include <stdio.h>

#define delta sizeof(char) 

int arr[10];

int main()
{
    for( int i = 8; i - delta >= 0; i -delta )
    {
        printf("arr = %d\n",arr[i]);
    }
}
/*
 *代码运行状态： Output Limit Exceeded 
 */
ex2
#define KSIZE 1024
char kbuf[KSIZE];
/* Copy at most maxlen bytes from kernel region to user buffer */
int copy_from_kernel(void *user_dest, int maxlen) {
    int len = KSIZE < maxlen ? KSIZE : maxlen;
    memcpy(user_dest, kbuf, len);
    return len;
}

/* Declaration of library function memcpy */
void *memcpy(void *dest, void *src, size_t n);

/* Malicious Usage */
void getstuff() {
    char mybuf[MSIZE];
    copy_from_kernel(mybuf, -512);
}

如果函数copy_from_kernel第二个参数传入负数, 在传入mcmcpy后转换为一个很大的无符号整数,
可能导致程序读取它没有被授权的内核内存区域.

2.3 整数运算

我们会看到整数运算有时会得到非直觉的结果, 这是由于计算机运算的有限性造成的.

2.3.1 无符号数加法
字长的有限
int main()
{
    unsigned char a = 255, b = 1;
    unsigned char c = a + b;
    printf("a + b = %d, c = %d", a+b, c);
}
/*
 *a + b = 256, c = 0
 */

如果把a, b解释为int类型, 结果应该为256, 但如果解释为相同大小的无符号数结果却为0.

上述结果是因为256超过了unsigned char表示的范围, 这称为溢出. 考虑两个$w$位的非负整数$x$, $y$.
$0 <= x + y <= 2^w - 2$, 也就是$x + y$的结果可能需要$w+1$位表示. 如果我们允许结果保持$w+1$位,
如果其在加上另一个数值, 我们可能需要$w+2$个位, 以此类推. 这种”字节膨胀”意味着想要完整保存
运算结果我们对字长不能有限制. 而实际运算中我们的做法是假设位长没有限制, 得到准确结果后
截断以w位保存.

无符号加法原理

引入符号$+^u_w$, u表示unsigned, w表示位长. x,y均为w位, $x +^u_w y$结果
f.png

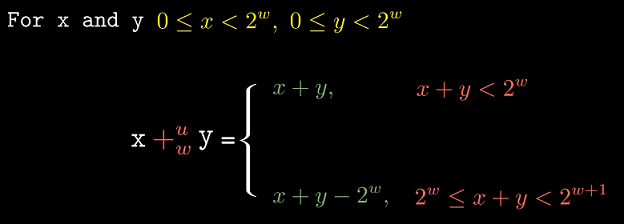
当$x +^u_w y$发生溢出时(需要额外位保存), 我们舍弃/截断额外位以保持$w$位.
g.png

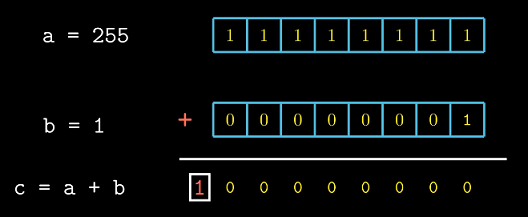
截断的额外位相当于$-2^w$. 或者对结果$mod 2^w$.

h.png

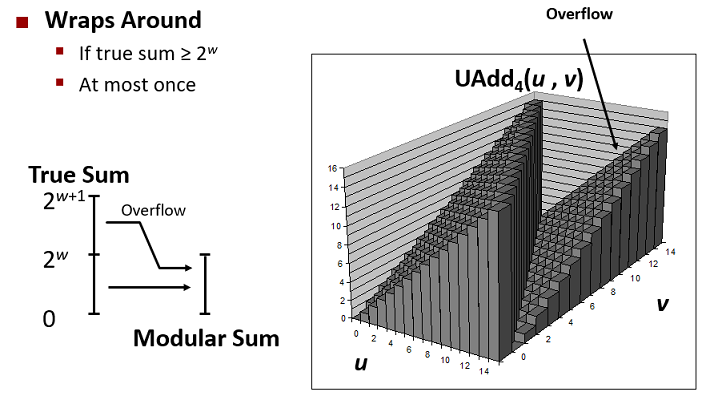
C中检测溢出

执行C程序时不会将溢出作为错误而发出信号, 不过我们有时希望检测是否发生溢出.

int uadd_ok(unsigned x, unsigned y)
{
    unsigned sum = x + y;
    return sum >= x + y;
}

如果没有发生溢出, $sum = x + y >= x$; 否则$sum = x + y - 2^w$, $y < 2^w$, 此时$sum < x$.

2.3.2 补码加法
基本思想

仍是通过将表示截断到$w$位来避免数据的不断扩张, 但结果却不想取模那么直观.定义
$x +^t_u y$为整数和$x + y$被截断为$w$位的结果, 并将结果解释为补码数.

补码加法原理

补码的溢出分为正/负溢出两种情况
2.png

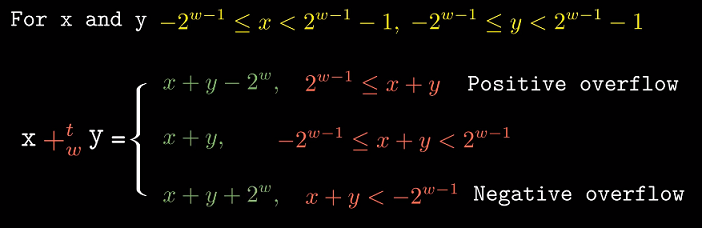
整数和补码加法间的关系.
3.png

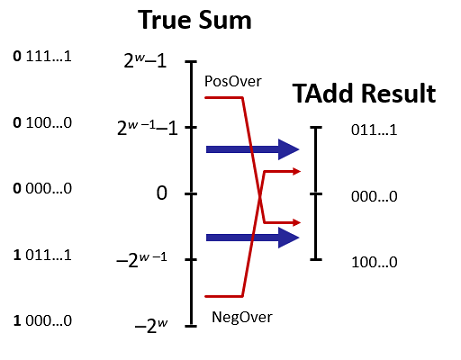
我们用两个例子在位级上理解补码加法.

int main()
{
    char a = 127, b = 1;
    char c = a + b;
    printf("c = %d\n",c);
}
/*
 *c = -128
 */

和的结果不是期望的128而是-128.
4.png
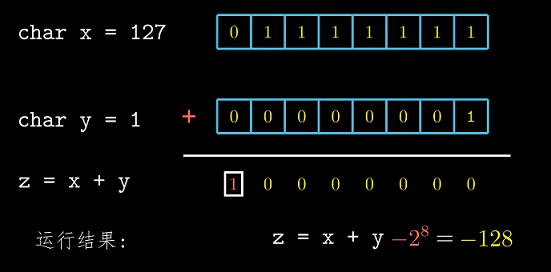
在位级表示上由于结果最高位1为负权, 所以得到负数的结果.

我们再观察$-128 + -1$的位级表示.
5.png
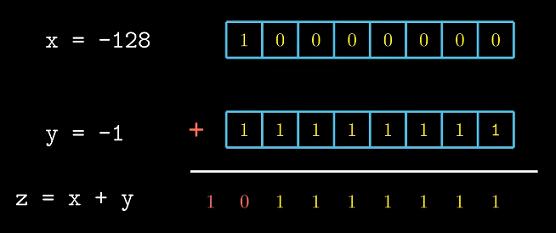
结果舍去了第$w+1$位, 而最高位由1变为0, 得到整数的结果.

位级

观察补码加法运算的位级表示, 可以发现实际上与无符号数相加在位级别完全相同.
$x +^t_w y = U2T_w(T2U_w(x) +^u_w T2U_w(y))$. 也就是补码运算可以在位级别上与
无符号整数完全相同, 只是最后对结果做出不同解释.

字长w = 4时不同补码之和的结果 :
6.png

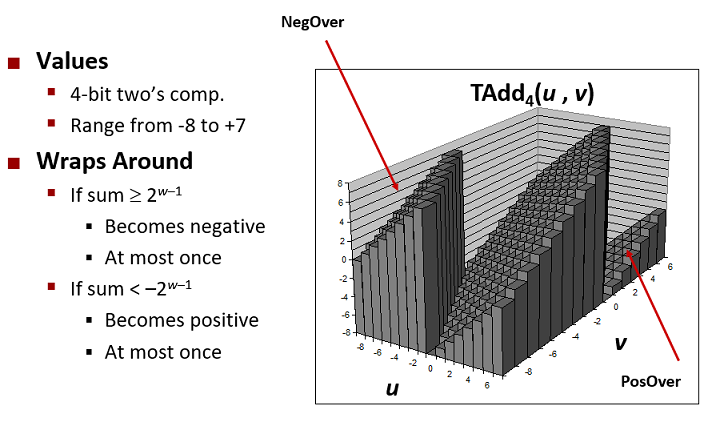
溢出检测
  • 正溢出 x > 0, y > 0, s = x + y <= 0
  • 负溢出 x < 0, y < -, s = x + y >= 0
习题

考虑下面检测溢出代码哪里出错了?

int add_ok(int x, int y)
{
    int sum = x + y;
    return (sum - x == y) && (sum - y == x);
}

这里我想到了一个反例INT_MIN, 希望你有更好的解释.

减法实现

逆元(相反数) : 对于$x$, 若$x’ + x == 0$, 称$x’$为$x$的加法逆元. 那么$y - x$ -> $y + x’$.
也就是减法的实现实际上就是找被减数的逆元.
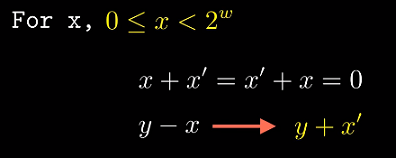
10.png

无符号数减法

对于无符号整数$0 <= x < 2^w$, 回想我们2.3给出的第一个例子, unsigned char的$a=255, b=1$.
$a + b = 0$. 也就是对于$a > 0%=$, 其加法逆元为$2^w$-a. 因为$s = a + a’ - 2^w = (a + 2^w -a-2^w)=0$
1.png

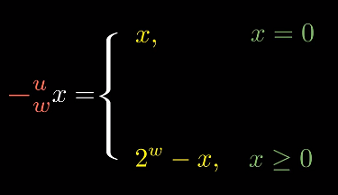
有符号数减法

补码数字$x$的逆元
2.png
这里需要注意由于补码正负号的非对称, $TMin$的逆元是其自身, 通过负溢出的方式得到0.

2.3.4 无符号乘法

范围在$0 <= x, y <= 2^w -1$内的整数乘积取值范围为0到$(2^w-1)^2 = 2^{2w}-2^{w+1}-1$, 可能需要
$2w$位存储.
3.png

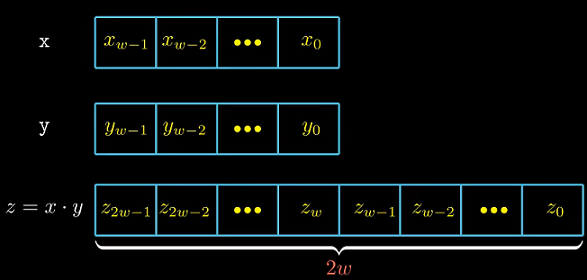
与加减运算相同, 为了防止位数膨胀, 这里只保留低$w$位, 等价于对$2^w$取模.
4.png

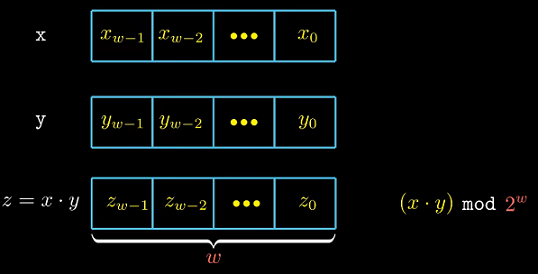
2.3.5 补码乘法
原理

补码的结果可能需要$2w$位保存, C中通过将$2w$的乘积结果截断为$2w$实现. 将一个补码数截断为$w$
位相当于先计算乘积值模$2^w$, 再把无符号数转换为补码.
也就是位级上补码乘积与无符号乘积相同, 区别在于对结果的解释.
5.png

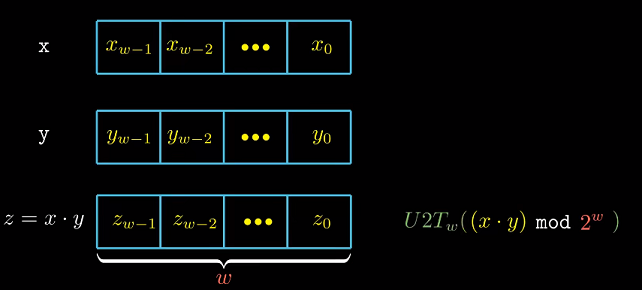
无符号和有符号乘法位级等价性

给定长度$w$位向量$X, Y$. $x, y$分别是补码解释; $x’, y’$分别是无符号数解释.
则证明 $T2B(x *^t_w y) = U2B(x’ *^u_w y’)$, 也就是$x*y$和$x’*y’$结果在位级别相同.

$x’ = x + x_{w-1}2^w, y’ = y + y_{w-1}2^w$, $( x’ * y’ ) mod 2^w = (x’ mod 2^w) * (y’ mod 2^w)$
在$mod 2^w$后, $x’ = x, y’ = y$
6.png

溢出检测
2.3.6 乘以常数

在大多机器上整数乘法指令相比加减、位级运算和移位相当慢, 所以编译器会试着用移位和加法运算的组合来
代替乘以常数因子的乘法. 我们首先考虑乘以2的情况, 接着概括成乘以任意常数.

乘以2的幂

乘以2的幂与左移
1.png

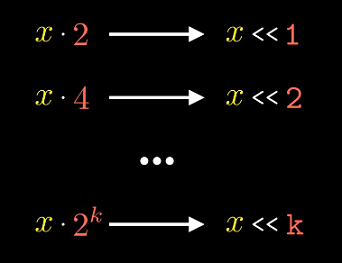
对于无符号整数, 左移k位后原先$X$的每一位的权重都从$2^i$->$2^{i+k}$
2.png

补码值的位级表示与无符号整数相同. 且乘以2的幂与左移都会溢出, 溢出后结果也相同.

乘以任意常数

3.png
考虑常数二进制从位n到位m有连续的1

  • (x<<n) + (x<<n-1) + … + (x<<m)
  • (x<<(n+1)) - (x<<m)
2.3.7 除以2的幂

在大多数机器上, 整数除法比整数乘法需要更长的时间. 除以2的幂可以用右移实现, 无符号数和
有符号数分别使用逻辑右移和算数右移实现.
4.png

向零舍入

整数除法在除不尽时结果总是向零舍入.
5.png

无符号数除以2的幂

无符号数右移结果如图.
6.png

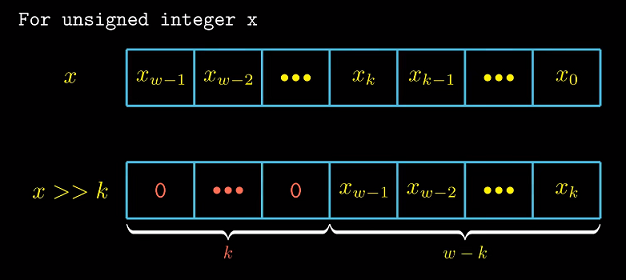
我们用$x1$和$x2$分别表示$x$的高$w-k$与低$k$位.
7.png

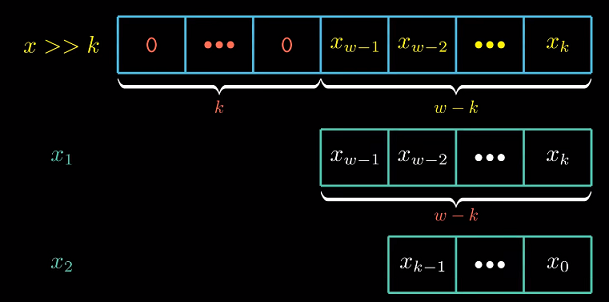
那么$x = 2^k * x1 + x2$. $x2$是k位无符号数, $0<= x2 < 2^k$, $x / 2^k = x1$, 与左移结果相同.
8.png

补码数除以2的幂

当符号位为0时, 右移结果与无符号数相同. 所以除以2的幂等价于右移.
当符号位为1时, 右移结果相当于$x/2^k$的向下舍入, 也就是向$-\infty$舍入而不是向$0$舍入.
1.png

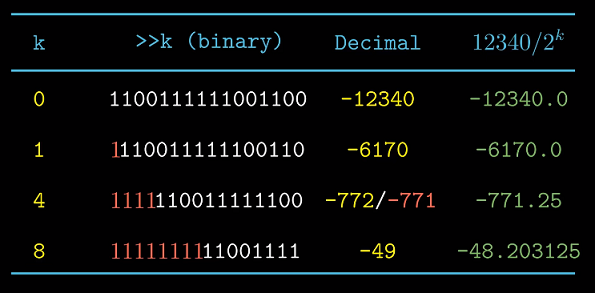
我们通过在移位前加入一个偏置bias来修正这种不合适的舍入.
偏置量 : 用到了我们在C中也可能遇到的将int除法的下取整->上取整. 方法
是在被除数上加上(除数-1).$\lceil x/y \rceil$ = $\lfloor (x+y-1)/y \rfloor$.
设$x = qy + r, 0<=r<y$. 那么 $\lfloor (x+y-1)/y \rfloor$ = $\lfloor (qy + r + y - 1)/y \rfloor$
= $q + \lfloor (r + y -1)/y \rfloor$

  • r = 0, $\lfloor (x+y-1)/y \rfloor$ = q + 0, 整除
  • 否则, $\lfloor (x+y-1)/y \rfloor$ = q + 1

这里$x/2^k$, 所以偏移量为$2^k-1$
2.png 

    (x < 0 ? x + (1<<k)-1 : x) >> k
任意常数

与乘法不同, 我们不能用除以2的幂的除法来表示除以任意常数的除法.

2.4 浮点数

在本节中, 我们将看到IEEE浮点格式中数字是如何表示的. 我们还将探讨舍入(rounding)的问题. 然后
我们将探讨浮点数加法、乘法和关系运算符的数学属性.

2.4.1 二进制小数

首先理解含有小数值的二进制数字. 与十进制表示类似, 数字权的定义取决于小数点的位置, 在小数点
左边的数字的权是2的正幂; 在小数点右边的数字的权是2的负幂.
3.png

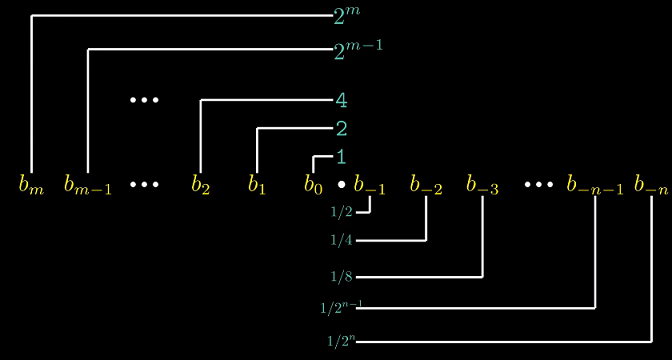
仅考虑有限长度的编码, 那么十进制不能准确表达无限循环小数/无理数. 类似的, 二进制表示法只能
精确表示形式为$x * 2^y$的数字, 我们只能近似表示它.

2.4.2 IEEE浮点表示
定点数 fixed point number

小数的定点表示 : 小数点固定不能移动. 整数可以认为是小数点固定在最低有效位的右边. 定点
表示法不能很有效的表示非常大的数字.

科学计数法 Scientific notation

IEEE浮点表示实际上就是以2为基底的科学计数法. 以10为基底的科学计数法 : 任何数字都要以
$a * 10^n$的形式表示, 其中$1<=a<10$.
科学计数法形式各部分的命名如下图所示. 我们把以科学计数法形式表示的数字称为规格化的(normalized);
否则称为非规格化的(denormoalized).

4.png

IEEE浮点标准

$V = (-1)^s * M * 2^E$

  • 符号(sign) s决定正(s=0)负(s=1). 对数值0的符号位作为特殊情况处理.

  • 尾数(signficand/mantissa) M是二进制小数, 范围$1$~$2-ε$, 表示数值部分.用符号ε表示一个很小的数.

  • 阶码(exponent) E对浮点数加权, 权重值为$2^E$

我们将浮点数划分为三个字段, 分别对这三个值编码 :

  • 一个单独符号位s直接编码符号s.

  • k位阶码字段$exp=e_{k-1}…e_0$编码E

  • n个小数字段$frac=f_{n-1}…f_0$编码尾数M.

C中的浮点数

5.png

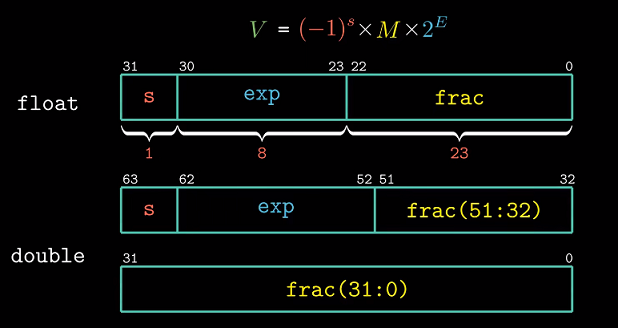
浮点数类型

根据$exp$的值, 我们将浮点数分为三类.

  1. 规格化的. $exp$不全为0或不全为1.

  2. 非规格化的. $exp$全为0.

  3. 特殊值

    • 无穷大. $exp$全为1, $frac$全为0.

    • NaN. $exp$全为1, $frac$不全为0.

规格化的值

$exp$不全为0或不全为1. 我们用e表示$exp$的无符号值, $1 <= e <= 2^k - 2$. 无符号的形式是为了
能够用无符号比较的方法应用在浮点数比较上.

  • 阶码值E = e - Bias. Bias = $2^{k-1} - 1$

Bias值 : e取值范围的中间点, 从非负整数到E可以表示负数.

我们用$f$表示小数字段$frac$表示的值.

  • 尾数M = $1.f_{n-1}…f_0$ = $1 + f$

M相比$f$有额外的1被叫做隐含1的表示. 因为对于规格化的二进制数字, 小数点左侧一定为1.
(十进制1~9, 而二进制只能为1)
所以我们可以不存储这个1, 这样我们就可以免费获得额外的一位. M的取值范围为$1$~$2-ε$

非规格化的值

$exp$全为0时. 有两个作用.

  1. $frac$字段全为0时表示0. (规格化数字由于隐含1不能表示0)
    1.jpg
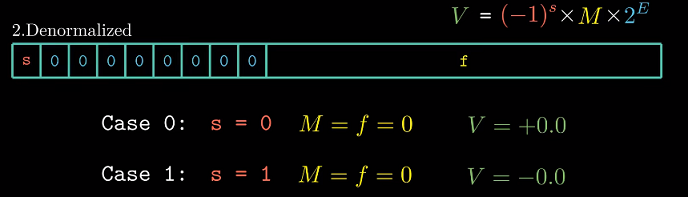
    $+0$和$-0$作为0的左右极限值.

  2. $frac$字段不为0时表示非常接近0数字. 编码方式 :

    • 阶码值E = 1 - bias. (不是0(e) - bias, 下面我们会看到这种设置是为了平滑的过度)
    • 尾数M = f (没有隐含的1, 为了表示数字0及接近0的数字)

这两种作用实际上统一可以由编码之后的数值$V = (-1)^s * M * 2^E$得到.

特殊值

表示浮点数溢出或非实数的情况.
2.jpg

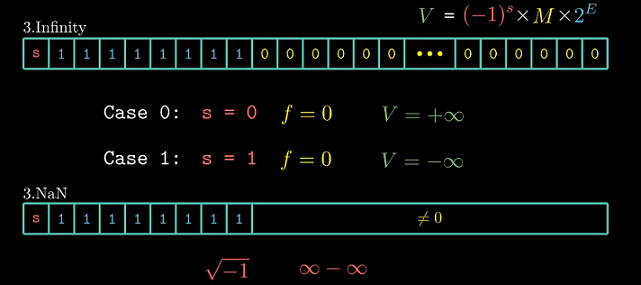
IEEE编码规则图示

3.png

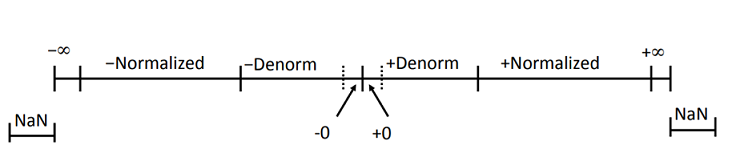
2.4.3 数字示例
8bit的浮点数

假定阶码位 k = 4, 小数位 n = 3. 此时偏置量$bias = 2^3 - 1 = 7$.
4.png

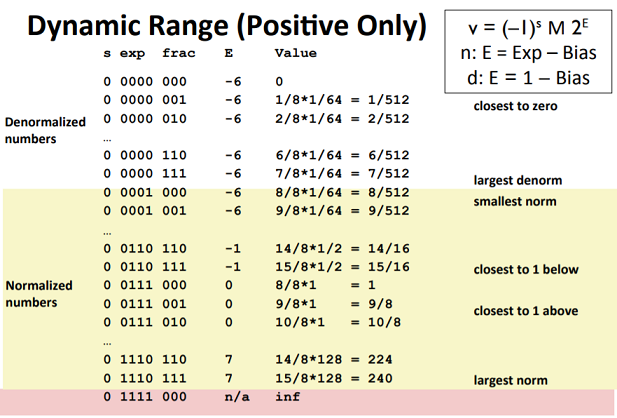
从上图可以观察到从非规格化数字到规格化数字的光滑转变, 这归功于对非规格化$E = 1 - bias$
而不是$0-bias$的定义. 随着阶码增大数值增大的间隔加倍. 当数值大于最大规划化数字240时,
浮点数溢出, 用$inf$表示.
这种表示还有一个有用的性质 : 如果把图中值的位表达式解释为无符号数, 它们的相对大小关系不变,
可以用无符号整数比较大小的方式比较浮点数大小. 这归功于$exp$无符号编码的方式.

12345

之前在2.1.3 寻址和字节顺序对比过整型数12345与单精度浮点数12345.0的二进制表示, 我们发现
移位后有一段数位是相同的.
5.png

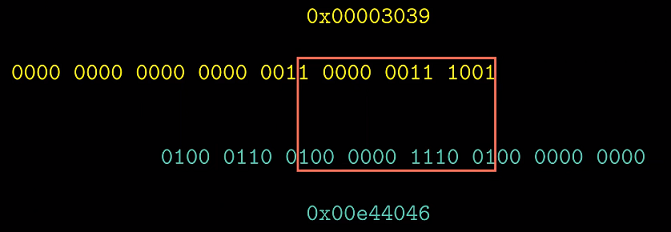
我们通过将整型数12345转换为浮点数12345.0了解这段匹配数位是如何产生的.

我们将整型数12345的二进制表示以规格化(科学计数法)规则表示, 移位后得到相应的E, 去掉首部
1后得到M. 通过转换后我们知道匹配的数段是整型数12345规格化表示后的小数部分.
12345.png

2.4.4 舍入 Rounding

因为表示方法限制了浮点数的范围和精度, 所以浮点运算只能近似地表示实数运算.
对于值$x$, 我们希望用期望的浮点数表示”最接近的”匹配值$x’$, 这就是舍入操作的任务.

舍入方式

舍入的一个关键问题是在两个可能值的中间确定舍入方向. 比如我们想把1.5舍入最近的整数, 应该
是1还是2呢 ? IEEE浮点格式定义了四种舍入方式.
6.png

向下舍入总是向可能值更小的方向舍入; 向上舍入总是向可能值更大的方向舍入. 而之前提到
的向零舍入在正数时向下, 负数时向上舍入.
7.png

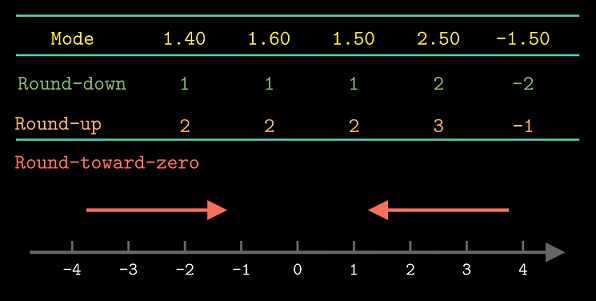
向偶舍入 也称向最近值舍入. 在值不是两个可能值的中点时, 采用类似4舍6入的方法, 向更
接近的值舍入; 当值在两个可能值的中点时, 采用最低有效位是偶数的规则舍入.

8.png

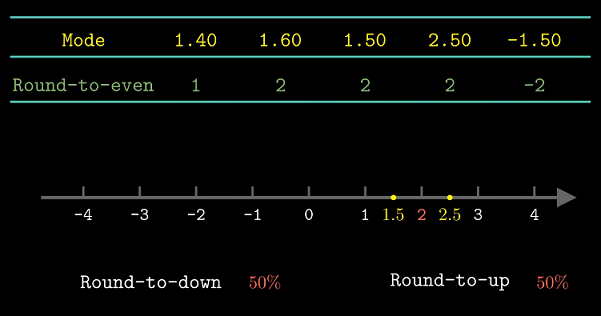
向偶舍入的方法在统计角度不会引入偏差, 向上舍入和向下舍入均有50%的可能.

进一步理解向偶舍入

向偶舍入也可对浮点数舍入, 我们只是简单考虑最低有效位的奇偶性. 以舍入到百分位为例.
9.png
注意此时考虑在两个百分位小数中间的情况.

向偶舍入同样能运用在二进制小数上. 我们将最低有效位0认为是偶数, 1认为是奇数.
10.png

2.4.5 浮点数运算

浮点运算规则与整数类似 : 假设我们有无限位(精确值)进行运算, 最后对实际运算的精确值进行舍入操作.
即一个运算⊙ 定义在实数上, 那么结果为$Round(X⊙ Y)$

浮点数乘法

浮点数$F1 * F2$的各个字段如下图.
1.png

浮点数加法

2.png
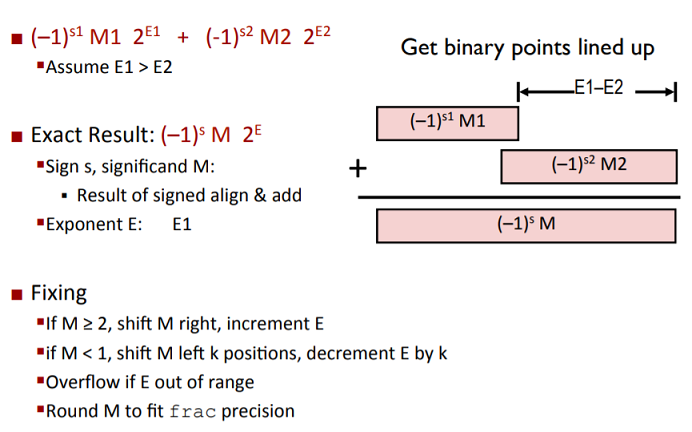
与十进制浮点数相加类似, 首先需要小数点对齐, 这里通过较小数左移小数点实现. 如果左移超出
范围就可能发生舍入.

浮点数乘法的数学属性

  • 可交换

  • 不具有结合性(可能发生溢出或者由于舍入而失去精度)

  • 不可分配性

  • 单调性(数字很大也不会改变符号而是溢出至inf, 不同于整数乘法) almost不包括inf/NaN

浮点数加法的数学属性

  • 可交换

  • 不可结合(由于舍入而失去精度)

  • 单调性(两个大数相加不会改变符号而是溢出至inf, 不同于整数加法) almost不包括inf/NaN

3.png

2.4.6 C语言中的浮点数

C提供了两种不同点浮点数据类型 : 单精度float和双精度double. C中浮点数的舍入方式是向偶舍入.

int、float和double间的强制类型转换

有较小位长类型转换为较大位长类型不会丢失数据, 反之会丢失数据(丢失精度或发生溢出).注意这里
int有32位而float小数字段只有23位.

  1. int -> float 不会溢出, 但可能被舍入.
  2. int/float -> double 保留精确数值
  3. double -> float 溢出成inf/-inf, 或者舍入
  4. float/double -> int 值会向0舍入或者溢出

图片来源
浮点数视频
推荐观看

0 评论