超全经典排序大汇总

算法思想

将两个或多个有序序列合并为一个有序序列

注：

1. 二叉树的第 h 层最多有 $ 2^{h-1} $ 个结点，若树高为 h ，则应该满足 $ n <= 2^{ h-1} $ , 即 $ h - 1 = \lceil log{_2}n\rceil $, 即趟数 = $ \lceil log{_2}n\rceil $
2. 每趟归并时间复杂度为 $ O(n) $ ,则算法时间复杂度为 $ O(nlogn) $
3. 空间复杂度为 $ O(n) $ ,来自于辅助数组

时间复杂度

1. 最好 — $O（nlogn）$
2. 最坏 — $O(nlogn)$
3. 平均 — $O（nlogn）$

注：

归并排序分割子序列与初始序列无关，因此它的最好、最坏、平均时间复杂度均为 $O（nlogn）$

演示动画

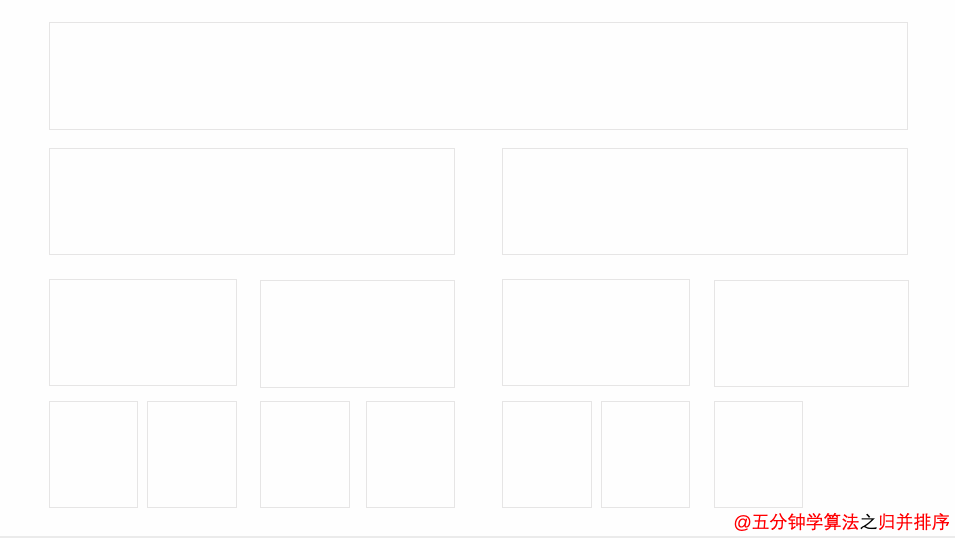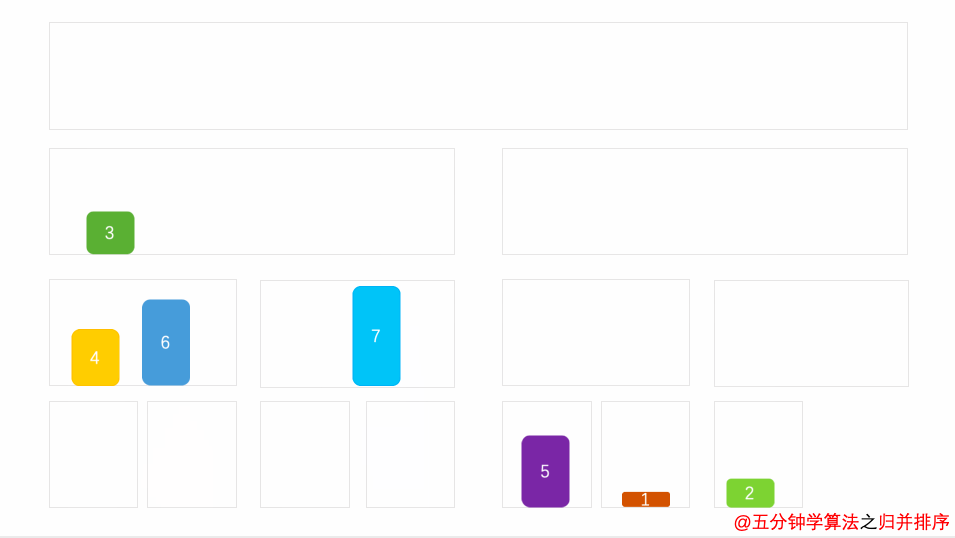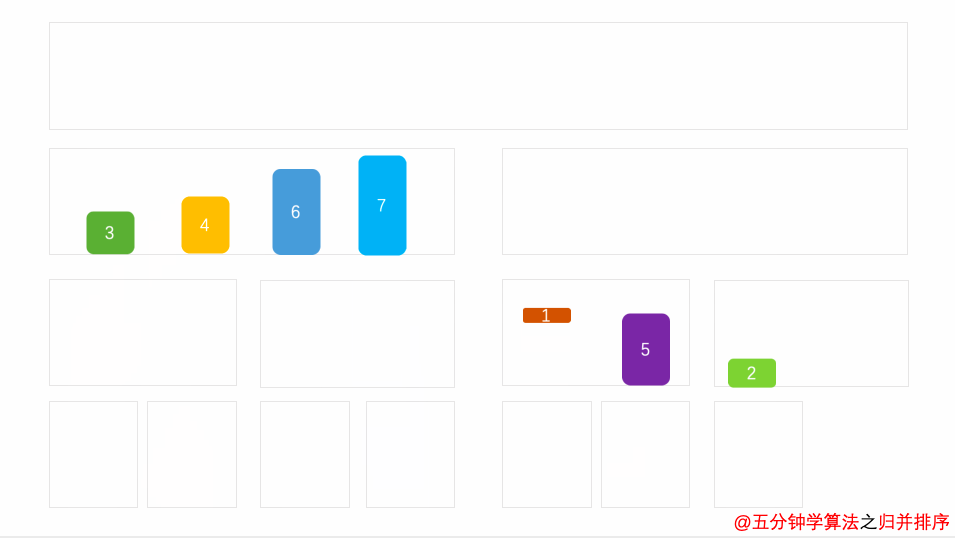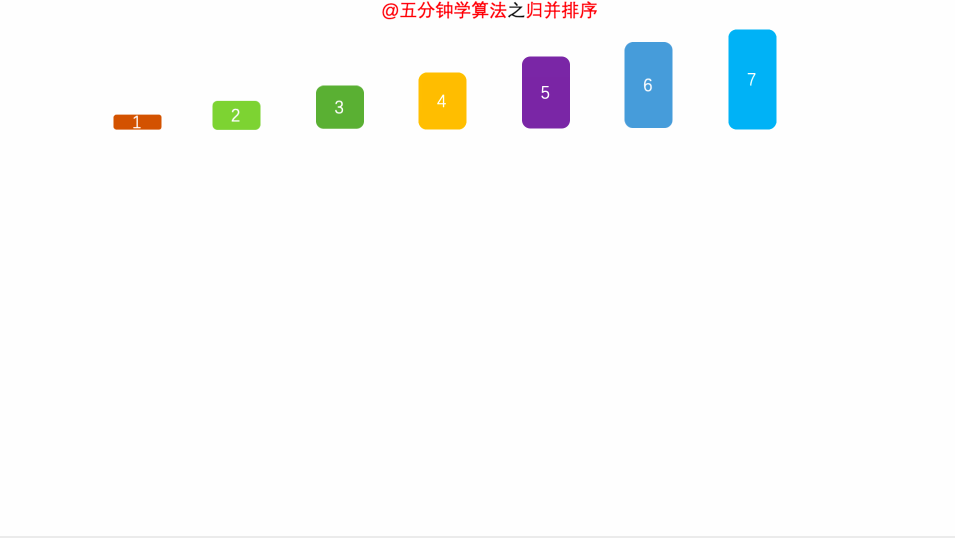
空间复杂度

需要一个辅助数组 ---- $O（n）$

稳定性

稳定

适用性

1. 顺序表
2. 链表

算法特点

1. 稳定排序
2. 可用于顺序结构，也可用于链式结构。使用链式结构不需要附加的存储空间，但递归实现时仍需要开辟相应的递归工作栈。
3. 一般而言，对于 $ n $ 个元素进行 $ k $ 路归并排序时，排序的趟数 $ m $ 满足 $k^m = n $, 从而 $ m = log{_k}n$ ，又考虑到 $ m $为整数，所以$ m = \lceil log{_k}n\rceil $

核心代码

//a[low ... mid] 和 a[mid + 1 ...high]各自有序,将二者归并 
void Merge(int a[], int low, int mid, int high){
    int k = low;
    int i = low, j = mid + 1;//左、右部分首元素 

    //将 a数组数据复制到 b数组 
    for(int i = low; i <= high; i ++) b[i] = a[i];

    //将 a[low ... mid] 和 a[mid + 1 ...high]归并
    while(i <= mid && j <= high){ 
        if(b[i] < b[j]) a[k ++] = b[i ++];
        else a[k ++] = b[j ++];
    }

    while(i <= mid) a[k ++] = b[i ++];//a数组已经枚举完 
    while(j <= high) a[k ++] = b[j ++];//b数组已经枚举完
}  

// 归并排序 
void MergeSort(int a[], int low, int high){//a[low ...high]
    if(low < high){
        int mid = low + high >> 1;//从中间划分 
        MergeSort(a, low, mid);//对左半部分进行归并排序 
        MergeSort(a, mid + 1, high);//对左半部分进行归并排序 
        Merge(a, low, mid, high);//归并 
    }
}

完整代码

#include <iostream> 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <fstream>

using namespace std;
const int N = 20;

int num;
int data[N],idx, b[N];

//a[low ... mid] 和 a[mid + 1 ...high]各自有序,将二者归并 
void Merge(int a[], int low, int mid, int high){
    int k = low;
    int i = low, j = mid + 1;//左、右部分首元素 

    //将 a数组数据复制到 b数组 
    for(int i = low; i <= high; i ++) b[i] = a[i];

    //将 a[low ... mid] 和 a[mid + 1 ...high]归并
    while(i <= mid && j <= high){ 
        if(b[i] < b[j]) a[k ++] = b[i ++];
        else a[k ++] = b[j ++];
    }

    while(i <= mid) a[k ++] = b[i ++];//a数组已经枚举完 
    while(j <= high) a[k ++] = b[j ++];//b数组已经枚举完
}  

// 归并排序 
void MergeSort(int a[], int low, int high){//a[low ...high]
    if(low < high){
        int mid = low + high >> 1;//从中间划分 
        MergeSort(a, low, mid);//对左半部分进行归并排序 
        MergeSort(a, mid + 1, high);//对左半部分进行归并排序 
        Merge(a, low, mid, high);//归并 
    }
}

int main(){
    //打开文件 
    ifstream infile;
    infile.open("D:\\学习\\数据结构\\第8章排序\\in.txt", ios::in);

    //写文件 
    ofstream outfile;
    outfile.open("D:\\学习\\数据结构\\第8章排序\\out.txt", ios::out);

    if(!infile.is_open()){//判断文件打开是否成功 
        cout << "file open failure!" << endl;
    }

    infile >> num;//读取元素个数 
    while(num --){//将文件中的元素复制到data[1...n] 数组中
        infile >> data[idx ++];
    }

    cout << "排序前元素序列：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    cout << "使用sort函数排序后序列: " << endl;
    sort(data, data + idx ); //sort排序区间左闭右开 
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    MergeSort(data, 0, idx - 1);
    cout << "使用堆排序后序列为：" << endl;
    for(int i = 0; i < idx; i ++) cout << data[i] << ' '; cout << endl;

    num = idx, idx = 0, outfile << num << endl;//写入数据数num以及在行末写入\n 
    while(num --){
        outfile << data[++ idx] << ' ';//将排序后的数据写到文件中 
    }
    outfile << endl;//向文件末尾写入\n结束符 

    //关闭文件 
    infile.close();
    outfile.close();
    return 0;
}

输入数据(in.txt)

10
13 69 86 99 59 23 64 32 86 72

输出数据(out.txt)

10
13 23 32 59 64 69 72 86 86 99