发现现在互联网公司面试很喜欢问智力题，没有准备的话容易一头雾水，总结了一些常见的题。

1、沙漏问题☆☆☆☆☆

有一个能计时6分钟的小沙漏和一个能计时8分钟的大沙漏，如何计时10分钟？

• 两个沙漏同时倒置开始计时，等小沙漏漏完，大沙漏还剩2分钟，这时倒置小沙漏继续计时；
• 大沙漏漏完小沙漏还剩4分钟，再把大沙漏倒置继续计时；
• 小沙漏漏完大沙漏还剩4分钟，这时准备工作已经完毕；
• 等待大沙漏漏完（4分钟）+ 小沙漏（6分钟） = 10分钟。

2、赛马问题（谷歌，腾讯）☆☆☆

64匹马，8个跑道，问最少比赛多少场，可以选出跑得最快的4匹马？

• 64匹马分8组进行比赛，记录成绩；
• 将每组第一名集合起来进行一次比赛，这是第9场；
• 保留前四名赛马所在的组，其余组淘汰；
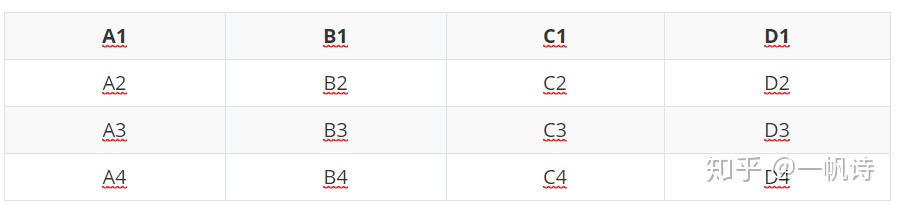
• 将前四名所在的组分别编号为A、B、C、D，进一步淘汰掉B4、C3、C4、D2、D3、D4这六匹马，因为它们不可能是TOP4，又因为A1已经确定为TOP1，故还需要在剩下的9匹马中选出前3，如图所示；
• 目前9匹马的情况是：A2 > A3 > A4，B1 > B2 > B3，C1 > C2，D1，9匹马选出8匹来比，有两种选法，故最差的情况需要再比两场；
• 先让前8匹马跑一场（不包括D1），此时重点关注C1这匹马，若C1排名第3及以后，则可以直接确定前TOP4，总共跑了10场；若C1排名第2时，推知B1第1，还需要再赛一场以确定C2、C3与D1中谁是TOP4，总共需要跑11场。

这是我目前见过最复杂的智力题了，需要进行大量分析。

3、老鼠与毒药问题（微软、腾讯）☆☆☆

有1000瓶水，其中一瓶有毒，只要老鼠喝下一小口毒水1天后就会死亡，你只有1天时间和10只老鼠，如何检验出哪一瓶水有毒？

• 2的每10次方对应10的每3次方，所以需要10只老鼠；
• 10只老鼠表示10个位，即能够表示0~1023的数字，大于1000瓶水，够了；
• 将1~1000号瓶子的编号改成二进制，分别喂给二进制表示中为1的位的老鼠，比如第7瓶水表示为0000000111，那么就给最后三只老鼠喂第7瓶水；
• 第二天死亡的老鼠所组成的二进制数，即表示那瓶毒水的编号。

4、倒水问题（字节、腾讯、美团）☆☆☆☆☆

水资源无限，有3L和5L水桶各一个，如何取4L水？

• 3L桶倒满，再倒入5L桶，此时5L桶有3L，3L桶为空；
• 继续倒满3L桶，再倒入5L桶，直到5L桶倒满为止，此时3L桶还剩1L；
• 5L桶倒空，将3L桶的1L倒入5L桶，再取一满桶3L倒入即可。

变种题：5L桶与6L桶，如何取4L水？（字节）

5、买水问题

一瓶水一块钱，两个空瓶可以换一瓶水，问20块钱能喝到几瓶水？

• 先买20瓶水，得到20空瓶；
• 再换10瓶水，得到10空瓶；
• 再换5瓶水，得到5空瓶；
• 再换2瓶水，得到2空瓶，总共还剩3空瓶；
• 再换1瓶水，得到1空瓶，总共还剩2空瓶；
• 最后再换1瓶水，总共喝了：20+10+5+2+1+1=39瓶；
• 注意这里还有一个小技巧，我们手里目前还剩一个空瓶，这时候跟老板借一瓶水，喝完后把两个空瓶还给他，刚好抵消，即喝了40瓶水。

6、老虎吃羊问题（字节）

岛上有一百只老虎和一只羊，老虎可以吃草但更愿意吃羊。假设每次老虎吃完羊，自己就变成了羊，同时所有的老虎都很聪明，它们都想活下去，那么这只羊会不会被吃掉？

• 如果只有一只老虎和一只羊，羊会被吃掉；
• 如果有两只老虎和一只羊，羊不会被吃，因为一旦有一只老虎吃了羊，就变成了一虎一羊的局面，另一只老虎就会把变成羊的老虎吃掉；
• 如果有三只老虎和一只羊，羊会被吃掉，因为一旦有一只老虎吃了羊，就变成了二虎一羊的局面，此时羊不会被吃掉（即这只老虎变成的羊不会被吃）；
• 综上所述，如果老虎的数量是偶数那么羊不会被吃，老虎数量为奇数则羊会被吃。

7、烧绳子（字节、腾讯、百度、TPLink）☆☆☆☆☆

烧一根绳子需要一个小时，现有若干条相同的绳子，问如何计时15分钟？

• 点燃绳子A的一头，同时点燃绳子B的两头；
• 绳子B烧完的时候绳子A还剩一半，此时点燃绳子A的另一头开始计时；
• 15分钟绳子A烧完。

8、一条绳子砍两刀，能构成一个三角形的概率？（字节、腾讯）

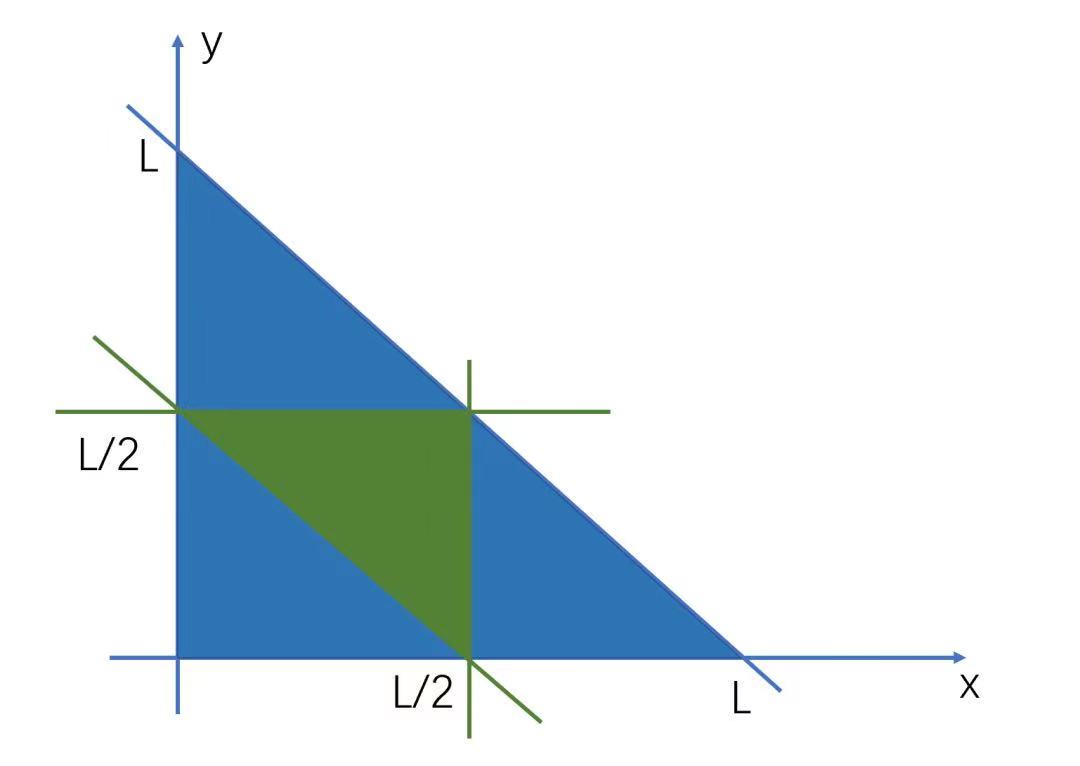
• 设绳子总长为L，分成三段为：x，y，L - x - y；
• 其中x > 0，y > 0， L - x - y > 0，取值范围如图中蓝色区域所示；
• 又因为任意两边之和要大于第三边，故有如下条件：
• x + y > L - x - y => y > -x + L / 2；
• x + (L - x - y) > y => y < L / 2;
• y + (L - x - y) > x => x < L / 2;
• 该区域为图中绿色区域，占蓝色区域的四分之一。

9、灯泡开关（字节压箱题）

一个圆环上有100个灯泡，灯泡有亮和暗两种状态，按一个灯泡的开关可以改变它和与它相邻两个灯泡的状态，设计一种算法，对于任意初始状态，使所有灯泡全亮。

• 将灯泡编号从1~100。从1循环到98，遇到暗的灯泡就按它下一个灯泡的开关，使之变亮，循环完毕后，1~98必然全亮；
• 99和100号灯泡有四种情况：亮亮、亮暗、暗亮、暗暗；
• 亮亮：已全亮；
• 亮暗、暗亮：达到只有一个为暗的状态；
• 暗暗：按下其中一个暗，两个暗都变成亮，之外的一个亮变成暗，达到只有一个为暗的状态；
• 目前是一个为暗的状态，剩下连续的99个灯泡都是亮的，这99个灯泡分成33组，按下每组中间那个灯泡，使得100个灯泡全变暗；
• 将所有全暗的灯泡全按一遍，即可达到全亮的状态。
• 扩展：全亮状态与全暗状态能够相互转换，方法是把每个灯泡开关全按一遍，即每个灯泡都改变了三次状态。

10、11223344问题（阿里）

有8个数，11223344，将其排列，要求结果满足两个1之间有1个数，两个2之间有2个数，两个3之间有3个数，两个4之间有4个数，问这个结果是多少？

• 这题不让写代码，要求动笔算，实际就是爆搜的过程；
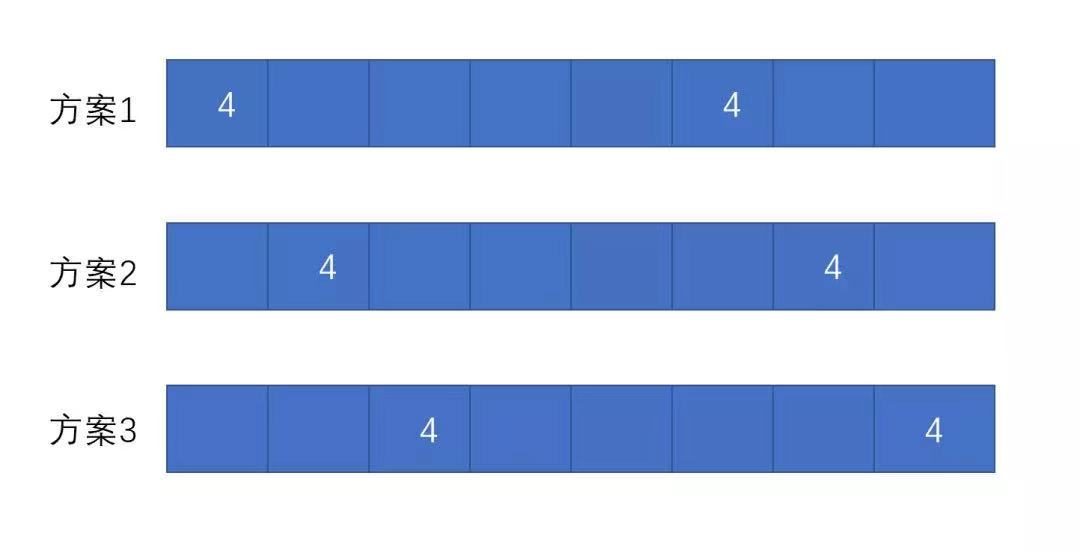
• 首先填4，因为填4可能的方案最少，如图一，又因为方案1与方案3相同，只是顺序不同，故填4其实只有两种方案；
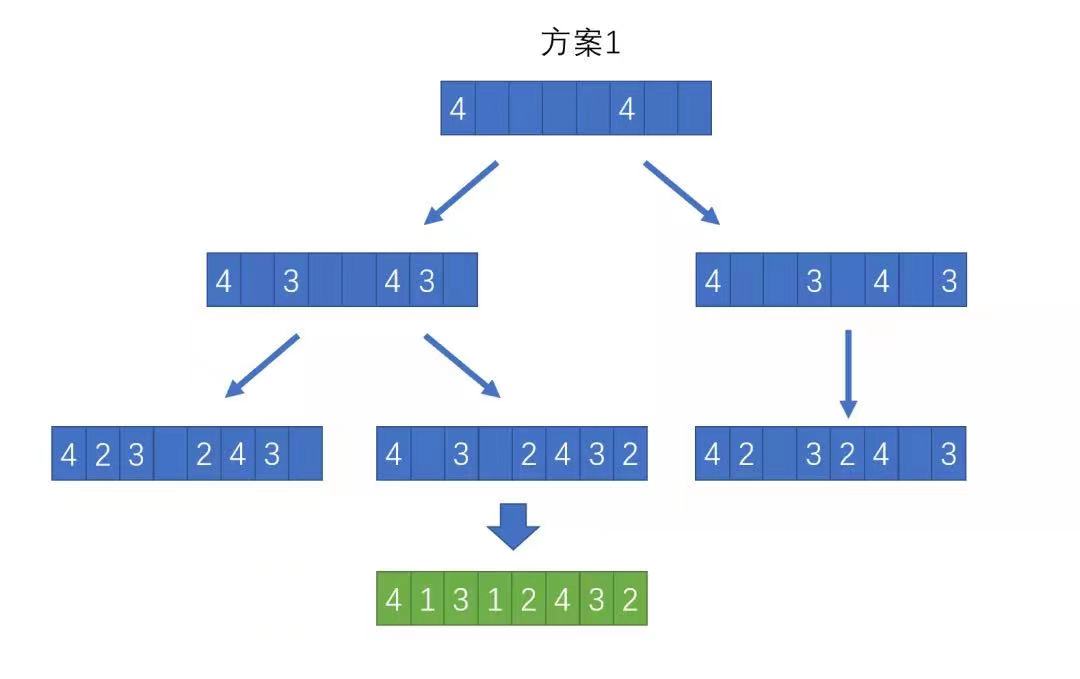
• 按照上面的思路填3、再填2、最后填1，如图二。

11、三人三鬼过河问题

有三个人跟三个鬼要过河，小船一次只能渡一个人和一个鬼、两个鬼或者两个人，无论在哪边岸上，只有是人比鬼少的情况下(如两鬼一人，三鬼两人，三鬼一人)人会被鬼吃掉，然而船又一定需要人或鬼操作才能航行(要有人或鬼划船)，问如何安全的把三人三鬼渡过河对岸?

• 先两鬼过去。一鬼回来。对面有一鬼。这边有三人两鬼；
• 再两鬼过去。一鬼回来。对面有两鬼。这边有三人一鬼；
• 再两人过去。一人一鬼回来。对面一人一鬼。这边两人两鬼；
• 最后两人过去。一鬼回来。对面三人。这边三鬼；
• 剩下的就三个鬼二个过去一个回来再接另外一鬼就行了。

12、砝码称重☆☆☆

有一个天平，九个砝码，其中一个砝码比另八个要轻一些，问至少要用天平称几次才能将轻的那个找出来？

• 需要称2次；
• 天平一边放三个砝码，哪边轻就在哪边，一样重就在剩下的三个砝码中；
• 现在已经锁定了三个砝码，天平一边放一个，哪边轻是哪个，一样重就是剩下的那个。

13、砝码称重2☆☆☆

十组砝码每组十个，每个砝码都是10g重，但是现在其中有一组砝码每个都只有9g重，现有一个能显示克数的秤，最少称几次能找到轻的那组？

• 称一次即可；
• 将砝码分组编号1~10，第1组拿1个砝码、第2组拿2个…第10组拿10个，全部放到秤上计算总克数X；
• Y = (1*10 + 2 * 10 + … + 10 * 10) - X = 550 - X，Y即为轻的那组的编号。

14、24小时内时针分针秒针重合了几次？

• 24小时内时针走了2圈，分针走了24圈，故时针与分针重合24 - 2 = 22次；
• 只要时针与分针重合，秒针一定有机会重合，所以总共重合22次。

15、先手必胜问题☆☆☆

100本书，每次能够拿1~5本，怎么拿能保证最后一次是你拿？

• 如果最后一次是我拿，那么上回合最少剩下6本；
• 只要保持每个回合结束后都剩下6的倍数，并且在这个回合中我拿的书和对方拿的书加起来为6本；
• 第一次我必须先手拿4本(100 % 6 = 4)，这不算在第一回合内。

16、掰巧克力问题

一块N * M大小的巧克力，每次掰一块的一行或一列，全部掰成 1 * 1 大小的巧克力需要掰多少次？

• N * M - 1次；
• 不管怎么掰，每次只能把一个大块掰成两个小块，即每次掰只能增加1块巧克力；
• 那么将1块巧克力掰成N * M块小巧克力就需要掰N * M - 1次。

17、辩论赛问题

1000个人参加辩论赛，1对1进行辩论，淘汰输掉的一方，问需要安排多少场比赛才能角出冠军？

• 每场辩论赛只能淘汰一个人，要淘汰999个人则需要安排999场比赛。

18、鸡蛋的硬度（谷歌）

有2个鸡蛋和100层的高楼，从不同楼层往下扔鸡蛋来测试鸡蛋的硬度。比如鸡蛋在第9层没有摔碎，在第10层摔碎了，那么鸡蛋的硬度就是9。问如何用最少的尝试次数，测试出鸡蛋不会摔碎的临界点？

• 不要一上来就直接说最优解，会暴露你做过这个题，应该循序渐进推理。

首先用朴素法：

• 从第一层开始往下扔，直到第N层鸡蛋碎了，那么鸡蛋的硬度就是N - 1；
• 效率太低，最坏情况下需要扔100次；

二分法：

• 从50楼扔下，碎了就再从1楼逐层扔到49楼，没碎就从51楼逐层扔到100楼；
• 效率仍然太低，最坏情况下需要扔50次；

平方根法：

• 100的平方根是10，那么就每10层扔一次；
• 最坏的情况是在第100层碎掉，需要扔9 + 10 = 19次，已经很接近最优解了。

最优解法：

• X * (X + 1) / 2 = 100，X为最优解，即X = 14。
• 该解法比较烧脑，感兴趣的可以看看这里 ： 100层楼扔鸡蛋

19、一亿数据获取前1000个最大值？☆☆☆

• 先取其中1000个数据建小根堆，堆顶为最小元素；
• 遍历剩下的数据，每个数据与堆顶元素比较，若大于堆顶元素则弹出堆顶元素，将该数据放入堆中，重构堆；
• 遍历完毕后堆中即是前1000个最大值。

20、一个圆上随机画两条弦，求相交的概率（百度）？☆☆☆

• 不要用数学公式去推导；
• 四个点确定两条线，在一个圆上取四个点；
• 四个点画两条线有三种情况，其中只有一种情况是相交的，故相交概率为三分之一。

21、分金块问题（字节）☆☆☆☆

工人为老板打工，工作七天可以获得一块金子，工人每天可以分得一点金子，老板必须每天发金子，不能多给，也不能少给，把这个金子切两刀，就可以每天给工人发工资，请问怎么切？

• 切两刀将金子分成三份，1/7、2/7、4/7；
• 工作第一天把1/7分给工人；
• 工作第二天把2/7分给工人，并要回1/7那块金子，工人有2/7的金子；
• 工作第三天 把1/7给工人 工人有3/7金子；
• 工作第四天 把前两块金子要回，给工人4/7的金子 工人有4/7的金子；
• 工作第五天把1/7分给工人 工人有5/7的金子；
• 工作第六天把2/7分给工人，并要回1/7那块金子，工人有6/7的金子；
• 工作第七天 把1/7给工人 工人有完整的金子；
• 扩展：如何给工人发15天的工资？把金块分成1/15、2/15、4/15、8/15。

22、大文件匹配 ☆☆☆

两个大文件，每行一个字符串，找交集。

• 这种大文件题首先要确定分而治之的思路，比如几十甚至几百个G的大文件，内存是不可能放得下的；
• 先遍历第一个文件A，对每个字符串使用哈希算法（或其他单向散列算法）计算出一个值，对这个值取余，具体对多少取余取决于你要将这个大文件分成多少个小文件，同时也要参考面试官给你的内存限制。比如我们将大文件分成1000份，可以表示为：hash(string) % 1000，然后根据所取得的值将该字符串存储到相应编号的小文件中（a1、a2、…、a1000）；
• 遍历文件B，使用同样的hash算法将每个字符串存储到相应编号的另外一千个小文件中（b1、b2、…、b1000），这样相同的字符串就会被映射到编号相同的小文件中；
• 遍历文件a1，对其建立哈希表，再遍历文件b1，若b1中的字符串出现在哈希表中，则该字符串属于交集；
• 对这1000个文件都循环使用上一步骤，即可得出总交集。

标☆的为高频题
参考自牛客网各路面经， 阿秀的博客 以及公众号《一个搬砖的胖子 》。