在看之前须知
如果没有接触过并查集，那么最好看完基础课并查集，或者看看 并查集1并查集2
推荐看完y总的进阶课并查集，或者边看进阶边看该文

朴素的并查集（y总基础课）

一般使用路径压缩的合并，按质合并 优化不是很大，时间不卡就不用按质合并了
朴素并查集就是从集合出发，考虑两个元素是否在同一个集合中
这样可以判断两个元素是否再同一个集合中，也可以找到不同集合个数

先来个水题
传送门 poj2524
这道题题意多组测试样例，每组给你n和m，n为学生编号，m为m行信息，每行都有i，j代表i，j信仰同一种
最后输出最多信仰不同的数目

那分析完之后就是很简单的求出集合个数

ac代码 poj2524 Ubiquitous Religions ;

再来一个水题
传送门 acwing 836.合并集合 ;
板子题，没什么好说的

ac代码 acwing 836.合并集合 ;

练习题
1.acwing 1249亲戚
注意读入输出，用scanf和printf，或者加速cin，cout，也可以直接写快读ac代码
2.acwing 1250格子游戏 ;
注意将每个点映射为一维点，然后判断是否联通即可ac代码
3.acwing 237程序自动分析
这道题注意离散化就行，先将相等的进行处理再处理不相等的情况ac代码

并查集扩展一，集合中元素数量

将一个集合中元素的数量与根节点绑定
那么，加一个表示数量的数组，只要在合并的时候加一下就可以了

传送门acwing 839.连通块中点的数量 ；

代码

#include <iostream>

using namespace std ;

const int N = 1e5 + 100 ;
int p[N],cnt[N] ;  //p代表,p[i]代表i的父节点是p[i], cnt[i]代表i为根的集合元素数量

int find(int x){
    if(x != p[x]) p[x] = find(p[x]) ;  //并查集，路径压缩
    return p[x] ;
}

int main(){
    int n,m ;
    cin >> n >> m ;

    for(int i = 1 ; i <= n ; i++){
        p[i] = i ;                   //初始化
        cnt[i] = 1 ;
    }

    while(m--){
        char op ;
        int a,b ;
        cin >> op ;
        if(op == 'C'){
            cin >> a >> b ;    
            int fa = find(a) , fb =find(b) ;  //找到根节点
            if(fa != fb){
                cnt[fb] += cnt[fa] ;  //合并时将fa合并到fb，最后fb是根节点，所以cnt[fb] += cnt[fa] ;
                p[fa] = fb ;         
            }
        }
        else{
            int t ;
            cin >> t ;
            if(t == 1){
                cin >> a >> b ;
                if(find(a) == find(b)) puts("Yes") ;
                else puts("No") ;
            }
            else{
                cin >> a ;
                cout << cnt[find(a)] << endl ;
            }
        }
    }

    return 0 ;
}

这里要注意，一定要先判断根节点是否相同，再进行合并，否则数量就会翻倍，，就是当根结点fa == fb 时，cnt就会翻倍

练习题
1.poj 1611 The Suspects
注意输入输出，ac代码poj 1611 The Suspects ;
~~~ 马上就做题，找到合适的题再加

并查集扩展二——带权并查集

带权并查集，由于并查集中的边是无向边，所以边权代表的关系一定是相对的，每个权代该节点与父节点的关系

先由一个例题来引出
传送门 acwing 食物链

题目分析一下就是有一个环形的食物链，每次告诉你，x，y是同类，还是x吃y
判断假话数目，以先说的话为真来判断

这里使用向量思维
在路径压缩的时候，也要处理d[]
那么已知x与父节点的关系d[x],与x的父节点与根节点的关系d[p[x]],就可以得到x与根结点的关系
x与根节点的关系是等于 d[x] + d[p[x]] ,
这里使用向量思维
x到root的向量等于x到父节点的向量加上父节点到根节点的关系

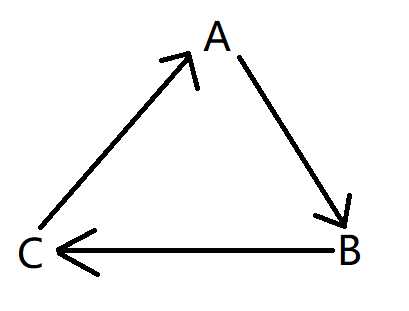
这是三个点的关系，构成了一个循环，箭头是由被捕食者到捕食者，那么沿着箭头x->y，1就代表x被y吃
2就代表y被x吃，0就代表x与y同类，，那么把x，p[x],root分别想象为这三个点中的一个（可以重复），
那么很容易得出x到root的向量等于x到父节点的向量加上父节点到根节点的向量


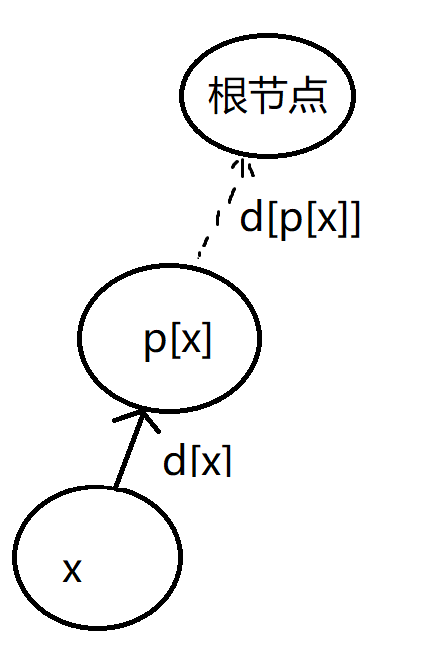
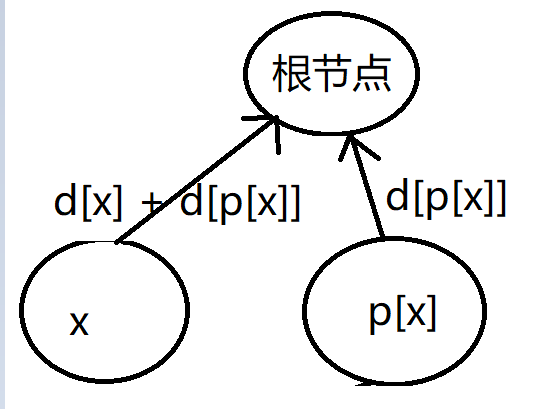
这个通过递归就可以实现，看下面代码递归处理

直接贴代码

#include <iostream>

using namespace std ;

const int N = 5e4 + 100 ;

int n,m ;
int p[N],d[N] ; //d 数组代表该节点和父节点的关系

//这里将d[i] = 1 ,代表x被父节点吃
//d[i] = 2 ,代表 x 吃父节点
//d[i] = 0 ,代表x与父节点是同类

int find(int x){  //查找根节点，路径压缩
    if(x != p[x]){
        int root = find(p[x]) ; //这里先把p[x], 找到p[x]
        d[x] = (d[x] + d[p[x]] ) % 3 ;    //x到根节点的关系表示为，x到父节点的关系加上父节点到根节点的关系
        p[x] = root ;
    }
    return p[x] ;
}

int main(){
    cin >> n >> m ;

    for(int i = 1;  i <= n ;i++){
        p[i] = i ;
    }

    int res = 0;
    while(m--){
        int op,x,y ;
        cin >> op >> x >> y ;
        if (x > n || y > n) res ++ ;   //越界肯定是谎话
        else{
            int fx = find(x),fy = find(y) ;
            if(op == 1){               //op == 1 ，代表是同类
                if(fx == fy && ((d[x] - d[y]) % 3 + 3 ) %  3 ) res ++ ;  //如果fx == fy
                            //在那个三角循环中，定一个点为fx，那么x到fx的距离dx，与y到fx的距离dy为
                            //那么只有dx与dy模三同余时，才是同类，否则不是同类
                            //所以((d[x] - d[y]) % 3 + 3 )%3 不等于0时，矛盾，res++ 
                else if (fx != fy){//如果fx ！= fy ，那么，还无法知道x，与y的关系，所以无矛盾，并构建关系
                    p[fx] = fy ; // 将fx指向fy，这是需要处理一下d[fx],使x与y是同类满足
                    d[fx] = ((d[y] - d[x]) % 3  + 3) % 3;  
                            //这里类别上面的思想，x到fx的距离为dx，y到fy的距离是dy，fx到fy的距离为？
                            //那么由上面得到的x与y是同类，那么 ， dx + ？（x到fy的距离） 与 dy 模三结果相同
                            // 那么 ？ = ((dy - dx) % 3 + 3 )%3
                }
            }
            else{
                if(fx == fy && ((d[x] - d[y] - 1 ) % 3 + 3 ) % 3 ) res ++ ; //同样的，判断x吃y，x到fx的距离
                                                            //比y到fy的距离多一再加上周期3的倍数
                else if(fx != fy){
                    p[fx] = fy ;
                    d[fx] = ((d[y] - d[x] + 1) % 3 + 3 )%3 ;  //同样的方法求出来问号
                                                    // dx + ? （x到fy的距离） 与 dy + 1 模三值相同 
                }
            }
        }
    }

    cout << res << endl ;

    return 0 ;
}

这里一定要引出向量思维csdn向量思维
可以看看里面思考权值是如何变化

练习题
1. acwing 238.银河英雄传
这是y总进阶课的讲题，ac代码
2. acwing 239 。奇偶游戏
注意离散化,将一个区间奇偶性问题改为两个前缀和奇偶性是否相同的问题 ac代码

然后如果边权模的数较小，还可以使用扩展域的并查集

扩展域并查集

先贴一个之前写的， 扩展域

单链表式并查集

这是一个并查集的另类思想了，偏离了并查集本意

p[i]代表从i开始右边第一个没有用过的数包括自己

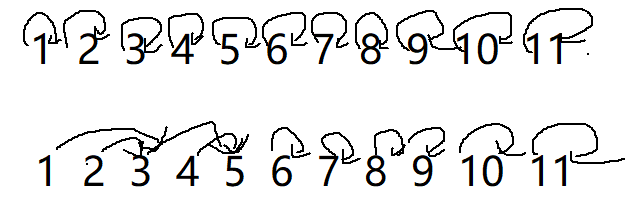
刚开始都是自环，后来会指向指会指向后面

传送门 [acwing 1242.修改数组](https://www.acwing.com/problem/content/1244/)

代码

#include <iostream>

using namespace std ;

const int N = 1e6 + 1e5 +100 ;

int n ;
int p[N] ;

int find(int x){
    if(x != p[x]) p[x] = find(p[x]) ;  //找到x右面第一次没有出现过的数
    return p[x] ;
}

int main(){
    cin >> n ;

    for(int i = 1 ; i < N ; i++) p[i] = i ; //初始化

    for(int i = 1 ; i <= n ; i++){
        int a;
        cin >> a ;
        int fa = find(a) ;           //找到后
        p[fa] = fa + 1 ;          //使用这个数，那么p[fa] 就该向右移一位，因为fa被使用
        cout<< fa << " " ;
    }
    return 0 ;
}

最后 你就可以在acwing中快乐地刷并查集题了 并查集