P1157 组合的输出
题目描述
排列与组合是常用的数学方法,其中组合就是从 n 个元素中抽出 r 个元素(不分顺序且 r≤n),我们可以简单地将 n 个元素理解为自然数 1,2,…,n,从中任取 r 个数。
现要求你输出所有组合。
例如 n=5,r=3,所有组合为:
123,124,125,134,135,145,234,235,245,345。
输入格式
一行两个自然数 n,r(1<n<21,0≤r≤n)。
输出格式
所有的组合,每一个组合占一行且其中的元素按由小到大的顺序排列,每个元素占三个字符的位置,所有的组合也按字典顺序。
注意哦!输出时,每个数字需要 3 个场宽。以 C++ 为例,你可以使用下列代码:
cout << setw(3) << x;
输出占 3 个场宽的数 x。注意你需要头文件 iomanip。
输入输出样例 #1
输入 #1
5 3
输出 #1
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
//组合跟排列有明显区别 排列需要判断位置是否使用
int g[N];
int f[N];
bool st[N];
int n, r;
void dfs(int u, int start)
{
if(u > r)
{
for(int i = 1; i <= r; i ++) cout << f[i] << " ";
cout << endl;
//注意结束递归
return;
}
for(int i = start; i <= n; i ++)
{
f[u] = i;
dfs(u + 1, i + 1);
}
}
int main()
{
cin >> n >> r;
for(int i = 1; i <= n; i ++) g[i] = i;
dfs(1, 1);
}
全排列的下一个排列
int i = n - 1, j = n;
while(i >= 1 && x[i] >= x[i + 1]) i --;
while(j >= 1 && x[i] >= x[j]) j --;
if(i <= 0)
{
reverse(x + 1, x + n + 1);
continue;
}
else
{
swap(x[i], x[j]);
reverse(x + i + 1, x + n + 1);
}
# P1149 [NOIP 2008 提高组] 火柴棒等式
## 题目描述
给你 $n$ 根火柴棍,你可以拼出多少个形如 $A+B=C$ 的等式?等式中的 $A$、$B$、$C$ 是用火柴棍拼出的整数(若该数非零,则最高位不能是 $0$)。用火柴棍拼数字 $0\sim9$ 的拼法如图所示:
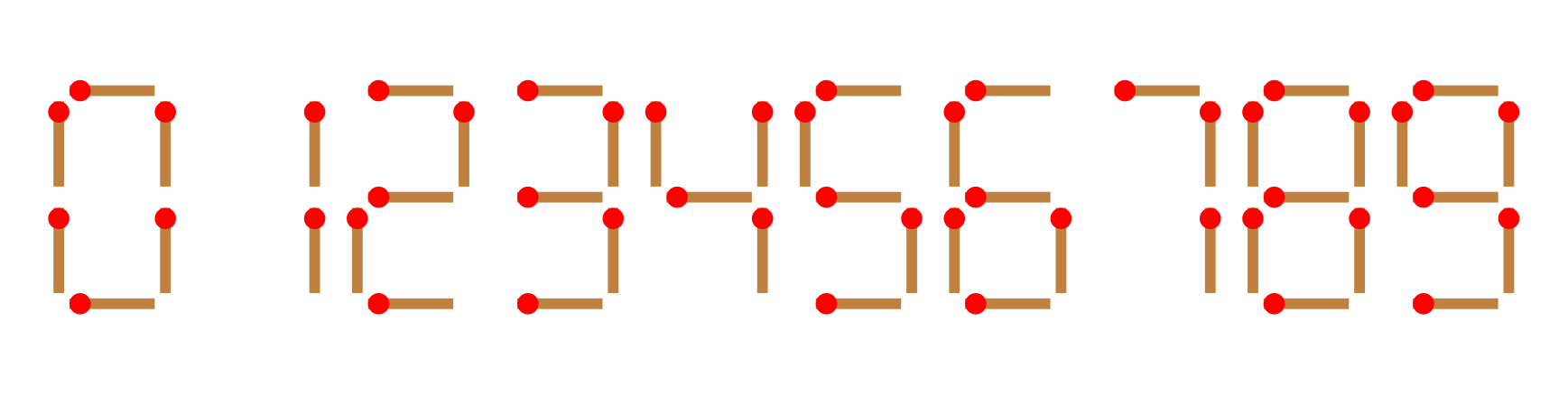
注意:
1. 加号与等号各自需要两根火柴棍;
2. 如果 $A\neq B$,则 $A+B=C$ 与 $B+A=C$ 视为不同的等式($A,B,C\geq0$);
3. $n$ 根火柴棍必须全部用上。
## 输入格式
一个整数 $n(1 \leq n\leq 24)$。
## 输出格式
一个整数,能拼成的不同等式的数目。
## 输入输出样例 #1
### 输入 #1
14
### 输出 #1
2
## 输入输出样例 #2
### 输入 #2
18
### 输出 #2
9
## 说明/提示
【输入输出样例 1 解释】
$2$ 个等式为 $0+1=1$ 和 $1+0=1$。
【输入输出样例 2 解释】
$9$ 个等式为
$0+4=4$、$0+11=11$、$1+10=11$、$2+2=4$、$2+7=9$、$4+0=4$、$7+2=9$、$10+1=11$、$11+0=11$。
noip2008 提高第二题
用10去推100 再去推1000
用空间换时间
int main()
{
int n, m;
int consume[1000] = {6, 2, 5, 5, 4, 5, 6, 3, 7, 6, 8, 4, 7, 7, 6, 7, 5, };
//0 1 2 3 4 5 6 7 8 9 10 11
for(int i = 10; i <= 100; i ++)
{
int a = consume[i / 10] + consume[i % 10];
consume[i] = a;
}
for(int i = 100; i < 1000; i ++)
{
int a = consume[i / 100] + consume[i / 10 % 10] + consume[i % 100 % 10];
consume[i] = a;
}
//cout << consume[200];
cin >> n;
int cnt = 0;
//int c = 0;
for(int i = 0; i < 1000; i ++)
{
int A = consume[i];
//if(i < 10) A = consume[i];
//else if(i >= 10 && i < 100) A = consume[i / 10] + consume[i % 10];
//else A = consume[i / 100] + consume[i / 10 % 10] + consume[i % 100 % 10];
for(int j = 0; j < 1000; j ++)
{
int B = consume[j];
for(int k = 0; k < 1000; k ++)
{
int C = consume[k];
if(A + B + C + 4 == n && i + j == k)
{
cout << i << "+" << j << "=" << k << endl;
cnt ++;
}
}
}
}
cout << cnt;
return 0;
}
P2036 [COCI 2008/2009 #2] PERKET
题目描述
Perket 是一种流行的美食。为了做好 Perket,厨师必须谨慎选择食材,以在保持传统风味的同时尽可能获得最全面的味道。你有 n 种可支配的配料。对于每一种配料,我们知道它们各自的酸度 s 和苦度 b。当我们添加配料时,总的酸度为每一种配料的酸度总乘积;总的苦度为每一种配料的苦度的总和。
众所周知,美食应该做到口感适中,所以我们希望选取配料,以使得酸度和苦度的绝对差最小。
另外,我们必须添加至少一种配料,因为没有任何食物以水为配料的。
输入格式
第一行一个整数 n,表示可供选用的食材种类数。
接下来 n 行,每行 2 个整数 si 和 bi,表示第 i 种食材的酸度和苦度。
输出格式
一行一个整数,表示可能的总酸度和总苦度的最小绝对差。
输入输出样例 #1
输入 #1
1
3 10
输出 #1
7
输入输出样例 #2
输入 #2
2
3 8
5 8
输出 #2
1
输入输出样例 #3
输入 #3
4
1 7
2 6
3 8
4 9
输出 #3
1
说明/提示
数据规模与约定
对于 100% 的数据,有 1≤n≤10,且将所有可用食材全部使用产生的总酸度和总苦度小于 1×109,酸度和苦度不同时为 1 和 0。
说明
- 本题满分 70 分。
- 题目译自 COCI2008-2009 CONTEST #2 PERKET,译者 @mnesia。
void dfs(int u, int k, int start)
{
if(u > k)
{
//if(x == 1 && y == 0) return;
int x = 1, y = 0;
for(int i = 1; i <= k; i ++)
{
x *= a[f[i]];
y += b[f[i]];
res = min(res, abs(x - y));
//cout << f[i] << " " << x << " " << y << " " << res << endl;
}
//res = min(res, abs(x - y));
//cout << endl;
return;
}
for(int i = start; i <= n; i ++)
{
f[u] = i;
dfs(u + 1, k, i + 1);
}
}
//如何求出n的组合数->>从也就是C(n, 1), C(n, 2), ...., C(n, n)
for(int i = 1; i <= n; i ++)
{
dfs(1, i, 1);
}
P2392 kkksc03考前临时抱佛脚
题目背景
kkksc03 的大学生活非常的颓废,平时根本不学习。但是,临近期末考试,他必须要开始抱佛脚,以求不挂科。
题目描述
这次期末考试,kkksc03 需要考 4 科。因此要开始刷习题集,每科都有一个习题集,分别有 s1,s2,s3,s4 道题目,完成每道题目需要一些时间,可能不等(A1,A2,…,As1,B1,B2,…,Bs2,C1,C2,…,Cs3,D1,D2,…,Ds4)。
kkksc03 有一个能力,他的左右两个大脑可以同时计算 2 道不同的题目,但是仅限于同一科。因此,kkksc03 必须一科一科的复习。
由于 kkksc03 还急着去处理洛谷的 bug,因此他希望尽快把事情做完,所以他希望知道能够完成复习的最短时间。
输入格式
本题包含 5 行数据:第 1 行,为四个正整数 s1,s2,s3,s4。
第 2 行,为 A1,A2,…,As1 共 s1 个数,表示第一科习题集每道题目所消耗的时间。
第 3 行,为 B1,B2,…,Bs2 共 s2 个数。
第 4 行,为 C1,C2,…,Cs3 共 s3 个数。
第 5 行,为 D1,D2,…,Ds4 共 s4 个数,意思均同上。
输出格式
输出一行,为复习完毕最短时间。
输入输出样例 #1
输入 #1
1 2 1 3
5
4 3
6
2 4 3
输出 #1
20
说明/提示
1≤s1,s2,s3,s4≤20。
1≤A1,A2,…,As1,B1,B2,…,Bs2,C1,C2,…,Cs3,D1,D2,…,Ds4≤60。
这里的问题可以理解为 左脑所花费的时间加上右脑所花费的时间 因此 原本数组的总时间等于左脑所花费的时间加上右脑所花费的时间
那么理想状态下取左脑所花费的时间, 右脑所花费的时间最大的一部分就行 因此这里就是在数据集合之中取子集尽可能优化那么这个优化值是什么——> 最理想的是一人一半即总数的一半
因此可以用01背包问题的思路来进行接近求解花费一半的时间
最后的结果就是 max(f[sum / 2], sum - f[sum / 2])
int solve(int s, int t[])
{
if(s == 1) return t[1];
int sum = 0;
int ans = 0;
for(int i = 1; i <= s; i ++) sum += t[i];
memset(f, 0, sizeof(f));
//cout << sum;
for(int i = 1; i <= s; i ++)
{
for(int j = sum; j >= t[i]; j --)
{
f[j] = max(f[j], f[j - t[i]] + t[i]);
}
}
//for(int i = 1; i <= sum; i ++ ) cout << f[i] << " ";
ans = max(f[sum / 2], sum - f[sum / 2]);
return ans;
}
P1217 [USACO1.5] 回文质数 Prime Palindromes
题目描述
因为 151 既是一个质数又是一个回文数(从左到右和从右到左是看一样的),所以 151 是回文质数。
写一个程序来找出范围 [a,b](5≤a<b≤100,000,000)(一亿)间的所有回文质数。
输入格式
第一行输入两个正整数 a 和 b。
输出格式
输出一个回文质数的列表,一行一个。
输入输出样例 #1
输入 #1
5 500
输出 #1
5
7
11
101
131
151
181
191
313
353
373
383
说明/提示
Hint 1: Generate the palindromes and see if they are prime.
提示 1: 找出所有的回文数再判断它们是不是质数(素数).
Hint 2: Generate palindromes by combining digits properly. You might need more than one of the loops like below.
提示 2: 要产生正确的回文数,你可能需要几个像下面这样的循环。
题目翻译来自NOCOW。
USACO Training Section 1.5
产生长度为 5 的回文数:
for (d1 = 1; d1 <= 9; d1+=2) { // 只有奇数才会是素数
for (d2 = 0; d2 <= 9; d2++) {
for (d3 = 0; d3 <= 9; d3++) {
palindrome = 10000*d1 + 1000*d2 +100*d3 + 10*d2 + d1;//(处理回文数...)
}
}
}
bool flag(int x)
{
int num = x;
int k = 0;
while(num)
{
//temp *= temp;
int temp = num % 10;
k = k * 10 + temp;
num /= 10;
}
if(k == x) return true;
else return false;
}
void is_prime(int n)
{
int t = sqrt(n);
for(int i = 2; i <= n; i ++)
{
if(!st[i])
{
for(int j = i + i; j <= n; j += i)
{
st[j] = true;
}
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int a, b;
cin >> a >> b;
//回文数 偶数位一定是11的倍数
if(b >= 1e7) b = 9999999;
//
//if(b >= 1e9) b = 99999999;
if(a > b) return 0;
is_prime(b);
if(a % 2 == 0) a += 1;
for(int i = a; i <= b; i +=2)
{
if(!st[i] && flag(i)) cout << i << endl;
}
//cout << flag(111) << endl;
return 0;
}

