（接上篇）
原文的$\text{PDF}$所在网址：点击此处跳转

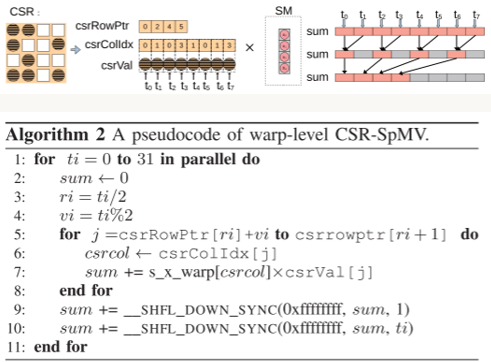
线程束级并行算法详解

$\text{CSR}$格式（$\text{DnsRow}$与此类似）：
1、每两个线程负责图块中一行的计算，乘向量$x$用共享内存区来存储；
2、每个线程包含一个分段累加和$sum$（分段求和思想），并和数组$y$的一个元素对应；
3、奇数号线程内的$sum$移动到偶数号线程内并累加；
4、$y$数组内分散的若干元素移动至开头连续的位置上。
步骤2和3可以用原语$\text{__shfl_down_sync}$来并行实现，它的作用是让$id$较小的线程从$id$较大的线程中获取数据。

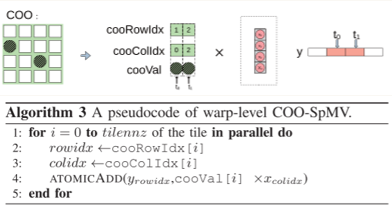
$\text{COO}$格式（$\text{DnsCol}$与此类似）：
1、每个线程单独负责一个矩阵元素，结果的y数组位于共享内存区；
2、线程计算完单个元素之后，将其累加到y数组的对应位置上。
并行算法有可能出现y的同一个位置被累加多次的情况，因此必须使用原子操作$\text{atomic_add}$来实现互斥的访问

$\text{Dense}$格式：
1、使用迭代方法，每一轮用一个线程束处理两行矩阵元素
2、每一轮迭代，将每个线程对dnsVal数组的访问位置后移，量为线程束的大小

$\text{ELL}$格式：
（原文中对该算法的描述比较模糊并且伪代码有误，本帖中将其细化并勘误）
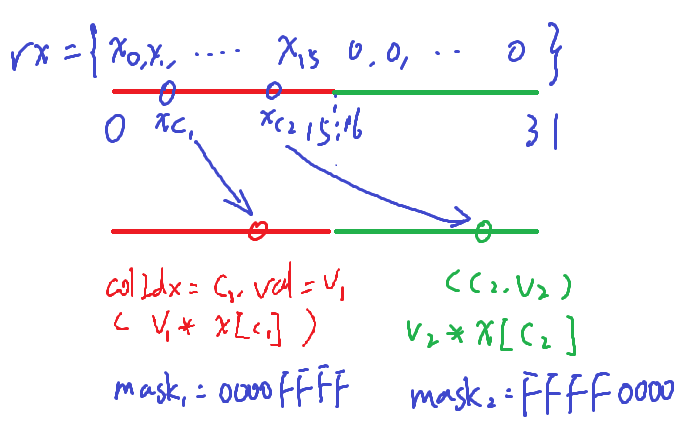
1、列下标与值的数组从行优先改为列优先，按此方法存储后，每个线程束内的线程分为均等的两组，对应$\text{ELL}$数组的两行

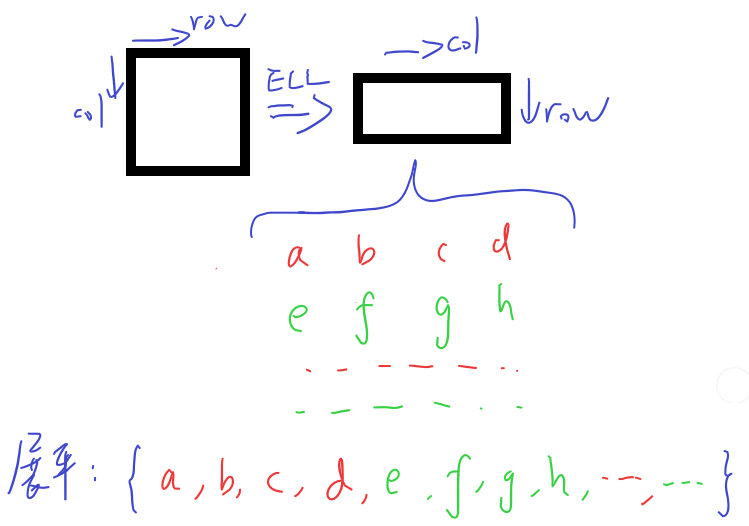
2、id较小的那一组线程，将乘向量x加载到寄存器中

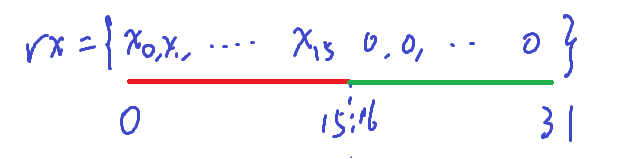
3、每个线程以迭代方式访问ELL数组中的元素，取得列下标c和真值v，并通过shfl_sync指令从其他线程获取x[c]，执行一次乘法累加（表达式：sum += v * x[c]）
4、迭代完成之后将16~31号线程中的sum集中到0~15号线程中

算法伪代码及勘误：

1、第4行，$j$的增量若未明确指出则默认为1，但实际的增量应为线程束大小32

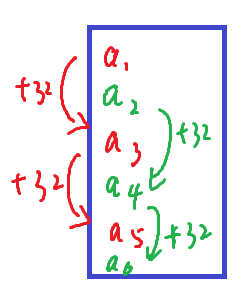
2、第6行，用$\text{__shfl_sync}$向线程束内全体线程广播时，掩码应当包含两组。线程束内的32个线程被赋予了$0\sim 31$的$id$，但是$x$的对应段只被加载进了能与原图块的$0\sim 15$列对应上的$0\sim 15$号线程。当接收数据的是$0\sim 15$号线程时，使用$0x0000ffff$作为掩码；而当接收数据的是$16\sim 31$号线程时，使用$0xffff0000$作为掩码

3、第8行，后面应当加上将$16\sim 31$号线程内的分段和$sum$累加到$0\sim 15$中的语句sum += __shfl_down_sync(0xffffffff, sum, 16)

$\text{HYB}$格式：即$\text{ELL、COO}$两者结合

块格式的选择方法

基于上述的分块存储和计算方式，有与之相对应的3种格式选择策略：
1、全部按CSR格式计算($\text{TileSpMV_CSR}$)

2、按流程图进行自适应选择($\text{TileSpMV_Adpt}$)

3、在方法2的基础上，将所有COO格式存储的图块一起存入另一个稀疏矩阵，并按CSR格式计算($\text{TileSpMV_DeferredCOO}$)

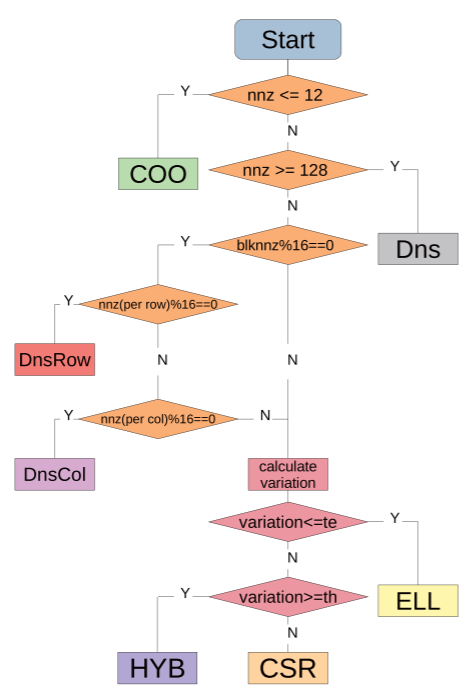
流程图中variation指变异系数（标准差与平均值之比），te和th分别为0.2和1

实验与性能分析

基于$\text{CUDA11.1}$，使用$\text{Turing}$架构的$\text{Titan RTX}和$\text{Ampere}$架构的$\text{A100}$两块GPU进行所有的实验，2757个实验矩阵均来自$\text{SuiteSparse}$矩阵库，元素类型统一为浮点型，行数与列数相等

对比实验包含两部分：三种选择策略$(AllCSR,Adpt,DeferredCOO)$的对比，本算法与另外三种算法$(MergeCSR,CSR5,BSR)$的对比，主要指标为计算速度，以每秒执行的浮点运算次数的$10^{-9}$倍来表征（即$GFlops$）。对比实验中还包含了多种方法之间的加速比。

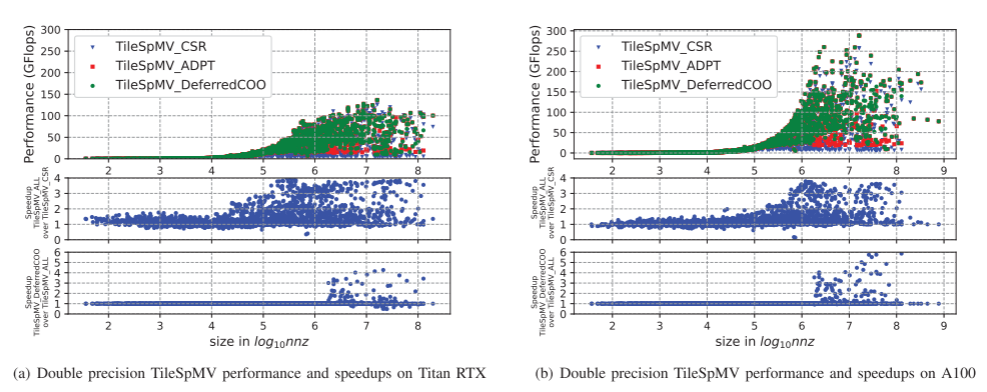
从三种选择策略之间的计算速度以及加速比来看，矩阵的非零元数量较少（$10^4$以下）时，自适应方式相较于全选$\text{CSR}$的方式虽有加速，但不明显，提取$\text{COO}$方式和自适应方式相比则几乎没有任何变化；非零元数量在$10^4\sim 10^6$之间时，自适应方式的加速效果有了明显的逐步提升，而提取$\text{COO}$方式仍然没有明显变化；当矩阵规模较大，非零元数量超过了$10^6$时，自适应和提取$\text{COO}$都有了较明显的加速

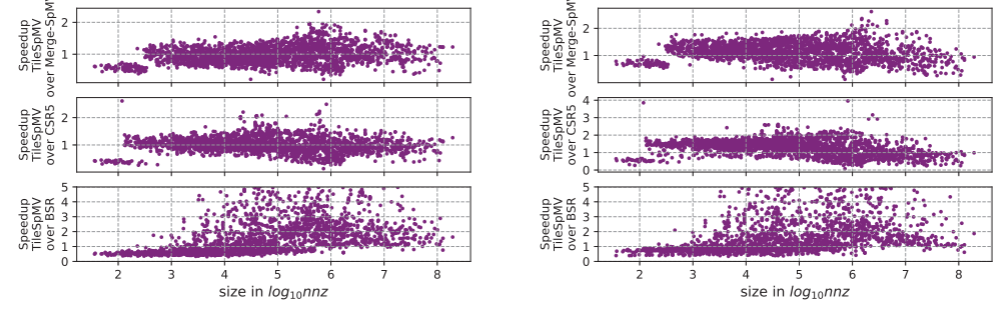
$\text{TileSpMV}$与另外3种方法的对比显示，矩阵规模较小（非零元数$1000$以下）时，$\text{TileSpMV}$的优化效果不明显，规模中等、较大（非零元数$10^3\sim 10^6$）时，$\text{TileSpMV}$相较于三种格式的优化效果都在逐渐提高，最大加速比分别达到$2.61$，$3.69$和$426.59$，在$10^6$基础上继续增大规模时，优化效果逐渐降低，但对比BSR的效果仍然最明显。在全部$2757$个矩阵中，$1813$个优于$\text{MergeCSR}$，$2040$个优于$\text{CSR5}$，$1638$个优于$\text{BSR}$

除了计算速度，本文还进行了两项对比：$\text{TileSpMV}$在最佳选择策略之下与$\text{CSR}$的空间占用情况对比，以及部分代表性矩阵预处理与计算的时间对比

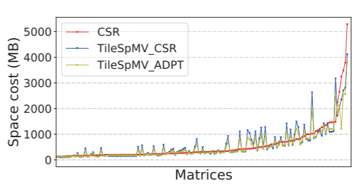
最大的150个矩阵中，$\text{TileSpMV}$在多数矩阵上比一般$\text{CSR}$格式占用了相同或者更少的空间，少数占用更多空间的主要原因是这些矩阵特别稀疏，但是划分后仍然为每个图块分配一个完整的行指针。

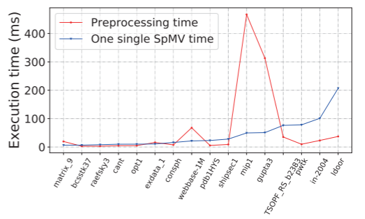
选取部分代表性矩阵样本分析了其预处理时间和计算时间，可以发现预处理时间可能会比计算时间高10倍以上，也可能比计算时间少。这取决于矩阵的稀疏度，结构，以及采用的若干自适应优化。

结论

本文提出的$\text{TileSpMV}$，可以通过利用稀疏矩阵的二维空间结构来加速$\text{GPU}$端的$\text{SpMV}$。该方法包含了划分与自适应，其中划分后对每个$\text{Tile}$的$\text{SpMV}$算法是线程束级的。通过对计算速度以及加速比的考察，特别是$10^4,10^6$这两个关键点，可以证明自适应方式和单独提取$\text{COO}$方式的有效性；而从该方法和$\text{MergeCSR,CSR5,BSR}$三种方法的对比来看，该方法自身的效率也得到了有效的提升。