0x11 栈
栈的运用
AcWing41. 包含min函数的栈
用一个辅助栈存所有可能成为答案的值，即维护两个栈，一个栈正常存，另一个栈存所有时刻的最小值。具体维护时如果新加入的值比辅助栈的栈顶小，就将它加入辅助栈，删除时判断两个栈栈顶是否相等，如果相等就让辅助栈栈顶出栈。
class MinStack {
public:
/** initialize your data structure here. */
stack<int> stk, minstk;
MinStack() {
}
void push(int x) {
stk.push(x);
if (minstk.empty() || x <= minstk.top())
minstk.push(x);
}
void pop() {
if (stk.top() == minstk.top()) minstk.pop();
stk.pop();
}
int top() {
return stk.top();
}
int getMin() {
return minstk.top();
}
};
AcWing128. 编辑器
使用两个栈分别维护光标左边和右边的字符，然后在做的时候维护一下前缀和数组 $S$，和当前前缀和最大值 $F$ 数组。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000010;
int stk1[N], top1, stk2[N], top2;
int f[N], s[N];
int main() {
int T; scanf("%d", &T);
f[0] = -0x3f3f3f3f;
while (T --) {
char c; int x;
scanf(" %c", &c);
if (c == 'I') {
scanf("%d", &x);
stk1[++ top1] = x;
s[top1] = s[top1 - 1] + x;
f[top1] = max(f[top1 - 1], s[top1]);
} else if (c == 'D') {
if (top1 > 0) top1 --;
} else if (c == 'L') {
if (top1 > 0)
stk2[++ top2] = stk1[top1 --];
} else if (c == 'R') {
if (top2 > 0) {
stk1[++ top1] = stk2[top2 --];
s[top1] = s[top1 - 1] + stk1[top1];
f[top1] = max(f[top1 - 1], s[top1]);
}
} else {
scanf("%d", &x);
printf("%d\n", f[x]);
}
}
return 0;
}
AcWing150. 括号画家
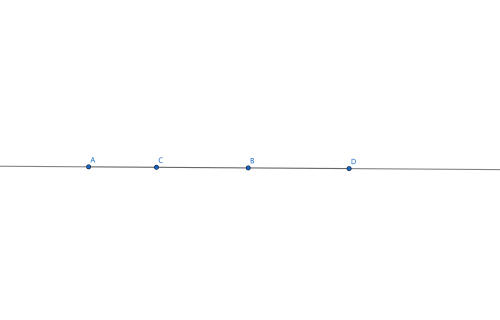
若下图，如果 $[A,B]$ 和 $[C,D]$ 都合法，那么 $[A,D]$ 一定合法。
证明：
将所有的左括号设为 $1$，右括号设为 $-1$，则任意合法序列一定满足任何前缀和大于等于 $0$ 且整个序列的总和为 $0$。
令 $[A,C], [C, B], [B, D]$ 的总和分别为 $x, y, z$ 。
那么 $\left\{\begin{matrix} & \\ x \geq 0 & \\ y \geq 0 & \\ z \geq 0 & \\ x + y = 0 & \\ y + z = 0 \end{matrix}\right.$
于是 $x = y = z = 0$ ，故$[A,D]$ 为括号序列。
我们可以从括号序列最开始进行匹配，把所有配对的删掉，然后记录最大的删掉长度。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
using namespace std;
const int N = 100010;
char s[N];
stack<int> stk;
bool compare(char a, char b) {
if (a == '(' && b == ')' || a == '[' && b == ']' || a == '{' && b == '}') return true;
return false;
}
int main() {
scanf("%s", s);
int n = strlen(s), res = 0;
for (int i = 0; i < n; i ++) {
if (stk.empty()) {
stk.push(i);
} else {
if (compare(s[stk.top()], s[i])) {
stk.pop();
} else {
stk.push(i);
}
}
if (!stk.empty()) res = max(res, i - stk.top());
else res = i + 1;
}
printf("%d\n", res);
return 0;
}
AcWing153. 双栈排序
引理1：如果只有一个栈，那么出入栈顺序一定是固定的。
引理2：对于两个数 $i,j(i \leq j)$ 当且仅当存在 $k > j > i$ 且 $q[k] < q[i] < q[j]$ 时，这两个数不能被放入一个栈中。
引理1的正确性是显然的，而对于引理2，这里引用一段 $yxc$ 的证明：
必要性：
如果有 $i < j < k$, 且 $q[k] < q[i] < q[j]$，则因为 $q[i]$ 和 $q[j]$ 的后面均存在一个更小的 $q[k]$，因此 $q[i]$ 和 $q[j]$ 都不能从栈中被弹出，所以从栈底到栈顶的元素就不是单调的降序了，那么弹出时得到的序列就会出现逆序对。因此 $q[i]$ 和 $q[j]$ 不能被分到同一个栈中。
充分性：
如果 $q[i]$ 和 $q[j]$ 不满足上述条件，则我们在操作过程中一定不会出现矛盾。
在操作过程中，如果当前要入栈的数是$q[j] $，那么此时：
所有大于 $q[j]$ 的元素，都一定在栈中；所有小于 $q[j]$ 的元素，比如 $q[i] < q[j]$，则由于后面不存在 $q[k] < q[i]$，因此 $q[i]$ 一定已经出栈；
所以此时将 $q[j]$ 压入栈中后，从栈底到栈顶仍然可以保持降序，因此整个进栈、出栈过程是可以顺利进行的。
通过上述引理，我们可以将原问题转换为二分图判定问题。具体的，我们给每个符合条件的 $i,j$ 都连一条边，然后通过染色法判定二分图。
接下来考虑最小字典序答案。我们发现在答案中 $ac$ 和 $bd$ 由于每个数插入的栈是唯一确定的，所以不能变换相对位置。$ab$ 和 $cd$ 由于引理1，所以也不能交换相对位置，所以我们只能要连续的 $ad$ 和 $bc$上下手段。
我们可以找出所有连续的 $ad$ 和 $bc$，然后排序即可。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
using namespace std;
const int N = 1010;
int n, a[N], f[N];
int color[N];
bool g[N][N];
bool dfs(int u, int c) {
color[u] = c;
for (int i = 1; i <= n; i ++) {
if (!g[u][i]) continue;
if (color[i]) {
if (color[i] == c) return false;
} else if (!dfs(i, 3 - c)) return false;
}
return true;
}
bool check(char a, char b) {
if (a > b) swap(a, b);
return a == 'a' && b == 'd' || a == 'b' && b == 'c';
}
int main() {
cin >> n;
for (int i = 1; i <= n; i ++) cin >> a[i];
f[n + 1] = n + 1;
for (int i = n; i; i --) f[i] = min(a[i], f[i + 1]);
for (int i = 1; i <= n; i ++)
for (int j = i + 1; j <= n; j ++)
if (a[i] < a[j] && f[j + 1] < a[i])
g[i][j] = g[j][i] = true;
for (int i = 1; i <= n; i ++)
if (!color[i] && !dfs(i, 1)) {
puts("0");
return 0;
}
string res;
stack<int> stk1, stk2;
for (int i = 1, cur = 1; i <= n; i ++) {
if (color[i] == 1) stk1.push(a[i]), res += 'a';
else stk2.push(a[i]), res += 'c';
while (stk1.size() && stk1.top() == cur || stk2.size() && stk2.top() == cur) {
if (stk1.size() && stk1.top() == cur) {
stk1.pop();
res += 'b';
} else {
stk2.pop();
res += 'd';
}
cur ++;
}
}
for (int i = 0; i < res.size(); ) {
int j = i + 1;
while (j < res.size() && check(res[i], res[j])) j ++;
sort(res.begin() + i, res.begin() + j);
i = j;
}
for (auto c : res) cout << c << ' ';
return 0;
}
栈与卡特兰数
AcWing130. 火车进出栈问题
我们把进栈看成 $1$，出栈看成 $0$，题目转换为 $n$ 个 $0$ 和 $n$ 个 $1$ 进行排列，且保证任何前缀中 $1$ 的个数大于 $0$ 的个数的方案数。
这就是卡特兰数的定义，所以我们只要求出：$ \frac{C^{n}_{2n}}{n + 1} = \frac{(2n)!}{n!n!(n+1)}$ 即可。
本题由于需要高精度，且时限卡的很紧，所以需要进行压位，同时我们要尽可能去掉非常缓慢的除法。
由于分母显然可以被分子整除，所以我们可以将分子分母同时分解质因数，然后用指数相减即可。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 120010;
int n, primes[N], cnt, powers[N];
bool st[N];
void get_primes(int n) {
for (int i = 2; i <= n; i ++)
if (!st[i]) {
primes[cnt ++] = i;
for (int j = i + i; j <= n; j += i)
st[j] = true;
}
}
int get(int n, int m) {
int s = 0;
while (n) {
s += n / m;
n /= m;
}
return s;
}
vector<LL> mul(vector<LL> &A, int b) {
vector<LL> C;
LL t = 0;
for (int i = 0; i < A.size(); i ++) {
t += A[i] * b;
C.push_back(t % 10000000000);
t /= 10000000000;
}
while (t) {
C.push_back(t % 10000000000);
t /= 10000000000;
}
return C;
}
int main() {
scanf("%d", &n);
get_primes(2 * n);
for (int i = 0; i < cnt; i ++) {
int p = primes[i];
powers[p] = get(n << 1, p) - get(n, p) * 2;
}
int k = n + 1;
for (int i = 0; i < cnt && primes[i] <= k; i ++) {
int p = primes[i], s = 0;
while (k % p == 0) {
k /= p;
s ++;
}
powers[p] -= s;
}
vector<LL> res;
res.push_back(1);
for (int i = 2; i <= n * 2; i ++)
for (int j = 1; j <= powers[i]; j ++)
res = mul(res, i);
printf("%lld", res.back());
for (int i = res.size() - 2; i >= 0; i --)
printf("%010lld", res[i]);
return 0;
}
表达式计算
AcWing151. 表达式计算4
最恶心的一集，面向评测大模拟。
首先得会 $y$ 总基础课教的模板，模板的大致思路是建立一个数字栈，一个符号栈，然后：
- 如果遇到一个数，将其压入数字栈
- 如果遇到左括号，将其入符号栈
- 如果遇到右括号，不断进行 eval 操作，直到栈顶为左括号，然后左括号出栈。
- 如果遇到运算符，只要栈顶符号的优先级不低于新的符号就一直 eval，最后把新符号进栈。
最后按照处理后缀表达式的方式进行处理。
本题中需要加上乘方运算，并且处理负号和多余括号的情况。
对于负号，只要负号前面是数字或右括号，那它就是减号，否则是负号。此时我们可以把 -x 变为 0-x，操作就方便多了。
对于多余括号，如果是左边的多余括号我们只需要在最后计算后缀表达式的时候不断删除多余括号即可。如果是右边的，我们就要在为它匹配左括号的过程中判断是否可以匹配。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
#include <unordered_map>
using namespace std;
stack<int> nums;
stack<char> op;
int pow(int a, int b) {
int res = 1;
while (b) {
if (b & 1) res = res * a;
b >>= 1;
a *= a;
}
return res;
}
void eval() {
int b = nums.top(); nums.pop();
int a = nums.top(); nums.pop();
char c = op.top(); op.pop();
int x;
if (c == '+') x = a + b;
else if (c == '-') x = a - b;
else if (c == '/') x = a / b;
else if (c == '*') x = a * b;
else x = pow(a, b);
nums.push(x);
}
int main() {
unordered_map<char, int> pr{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}, {'^', 3}};
string s;
cin >> s;
for (int i = 0; i < s.size(); i ++) {
auto c = s[i];
if ((c == '+' || c == '-') && !(i && (s[i - 1] >= '0' && s[i - 1] <= '9' || s[i - 1] == ')'))) {
if (c == '+') continue;
nums.push(0);
op.push(c);
} else if (isdigit(c)) {
int x = c - '0', j = i + 1;
while (j < s.size() && isdigit(s[j])) {
x = x * 10 + s[j] - '0';
j ++;
}
i = j - 1;
nums.push(x);
} else if (c == '(') {
op.push('(');
} else if (c == ')') {
while (op.size() && op.top() != '(') eval();
if (op.size()) op.pop();
} else {
while (op.size() && op.top() != '(' && pr[op.top()] >= pr[c]) eval();
op.push(c);
}
}
while (op.size()) {
if (op.top() == '(') op.pop();
else eval();
}
cout << nums.top() << endl;
return 0;
}
单调栈
AcWing131. 直方图中最大的矩形
考虑暴力解法，枚举第 $i$ 个矩形能向左和向右拓展到的长度，取最大的面积。所以我们可以预处理第 $i$ 个矩形能拓展到的左边界和右边界，再计算面积即可。
如何快速求出左边界和右边界呢？假设有 $i < j < k$ 且 $h[i] > h[j] < h[k]$，那么 $h[i]$ 是可以被忽略的，因为 $k$ 往左拓展的路上有一个很小的 $j$ 阻隔，所以 $k$ 到 $n$ 的所有矩形多不能拓展到 $i$，故而 $h[i]$ 可以被忽略。由此，我们可以用一个栈存所有 不被忽略 的值，而左边界就是我们的栈顶。
右边界类似于左边界，这里不过多赘述。总而言之，这就是我们的单调栈算法。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010;
int n, l[N], r[N], h[N];
int stk[N], top;
void work(int l[N]) {
top = 0;
h[0] = -1;
for (int i = 1; i <= n; i ++) {
while (h[i] <= h[stk[top]]) top --;
l[i] = stk[top];
stk[++ top] = i;
}
}
int main() {
while (scanf("%d", &n) == 1 && n) {
for (int i = 1; i <= n; i ++)
scanf("%d", &h[i]);
work(l);
reverse(h + 1, h + 1 + n);
work(r);
reverse(h + 1, h + 1 + n);
LL res = 0;
for (int i = 1, j = n; i <= n; i ++, j --)
res = max(res, h[i] * (n - r[j] + 1 - l[i] - 1ll));
printf("%lld\n", res);
}
return 0;
}
AcWing152. 城市游戏
类似于上一题，我们只要预处理一下 $w_{i, j}$ 代表 $(i,j)$ 同一列的上方有多少个 $F$，再跑单调栈即可。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
using namespace std;
const int N = 1010;
int n, m;
int w[N][N], l[N], r[N];
char a[N][N];
void work(int l[], int x) {
stack<int> stk;
stk.push(0);
w[x][0] = -1;
for (int i = 1; i <= m; i ++) {
while (w[x][i] <= w[x][stk.top()]) stk.pop();
l[i] = stk.top();
stk.push(i);
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++)
scanf(" %c", &a[i][j]);
for (int i = 1; i <= m; i ++)
for (int j = 1; j <= n; j ++) {
if (a[j][i] == 'R' || a[j - 1][i] == 'R') w[j][i] = 0;
else w[j][i] = w[j - 1][i];
w[j][i] += a[j][i] == 'F';
}
int res = -1;
for (int k = 1; k <= n; k ++) {
work(l, k);
reverse(w[k] + 1, w[k] + 1 + m);
work(r, k);
reverse(w[k] + 1, w[k] + 1 + m);
for (int i = 1, j = m; i <= m; i ++, j --)
res = max(res, (m - r[j] - l[i]) * w[k][i]);
}
printf("%d\n", res * 3);
return 0;
}
0x12 队列
队列运用
AcWing132. 小组队列
由于队列中同一组的人一定是抱团在一起的，所以我们可以用一个队列存小组的编号，然后开 $n$ 个队列存每个小组内的情况，进行维护即可。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
using namespace std;
typedef pair<int, int> PII;
const int N = 1010, M = 1000010;
int n, groups[N][N];
int main() {
int T = 0;
while (scanf("%d", &n) == 1 && n) {
T ++;
map<int, int> m, sum;
map<int, bool> inqueue;
queue <int> g, q[n + 5];
for (int i = 1; i <= n; i ++) {
int cnt; scanf("%d", &cnt);
for (int j = 1; j <= cnt; j ++) {
int x; scanf("%d", &x);
m[x] = i;
}
}
string s;
printf("Scenario #%d\n", T);
while (cin >> s) {
if (s == "ENQUEUE") {
int x; scanf("%d", &x);
int id = m[x];
if (inqueue[id] == true) {
q[id].push(x);
sum[id] ++;
} else {
inqueue[id] = true;
g.push(id);
q[id].push(x);
sum[id] = 1;
}
} else if (s == "DEQUEUE") {
int t = g.front();
if (sum[t] == 1) {
printf("%d\n", q[t].front());
q[t].pop();
g.pop();
sum[t] = 0;
inqueue[t] = false;
} else {
printf("%d\n", q[t].front());
q[t].pop();
sum[t] --;
}
} else {
break;
}
}
puts("");
}
return 0;
}
AcWing133. 蚯蚓
假设当前最大值为 $x$，那么会产生两只长为 $\left \lfloor px \right \rfloor$ 与 $x - \left \lfloor px \right \rfloor$ 的蚯蚓，然后所有的蚯蚓的长度加上 $q$。我们考虑曲线救国，即每次产生的蚯蚓长度都减去 $q$，然后记录一个偏移量 $delta$，使得每只蚯蚓的长度加上 $delta$ 就是真实数值。
具体的，起初，我们令 $delta = 0$，每次：
- 找到长度最长的一只蚯蚓，长度为 $x$，令 $x = x + delta$
- 插入 $\lfloor px \rfloor - delta - q$ 和 $x - \lfloor px \rfloor - delta - q$ 两只蚯蚓
- 令 $delta = delta + q$
由于每次需要 $O(n)$ 的时间寻找最大值，所以总时间复杂度是 $O(N^2)$ 的，不足以通过。
我们考虑如何快速求出集合的最大值。我们大胆猜想蚯蚓长度一定满足某种性质，可以证明对于两只长度为 $x_1$ 和 $x_2 + q$ 的蚯蚓，一定存在 $\lfloor px_1 \rfloor + q \geq \lfloor p(x_2 + q) \rfloor$ 且 $x_1 - \lfloor px_1 \rfloor + q \geq x_2 + q - \lfloor p(x_2 + q) \rfloor$。即若 $x_1$ 比 $x_2$ 先取出，那$x_1$ 分成的两只蚯蚓一定分别大于等于 $x_2 + q$ 分成的两只蚯蚓。
证明：
先证明 $x_1 - \lfloor px_1 \rfloor \geq x_2 - \lfloor px_2 \rfloor$
由于 $x_1 - x_2 \geq p(x_1 - x_2)$
所以 $\lfloor x_1 - x_2 + px_2 \rfloor \geq \lfloor px_1 \rfloor$
所以 $x_1 - x_2 + \lfloor px_2 \rfloor \geq \lfloor px_1 \rfloor$
从而 $x_1 - \lfloor px_1 \rfloor \geq x_2 - \lfloor px_1 \rfloor$
得证。
然后由于 $x_1 \geq x_2, 0 < p < q$ ，
所以 $px_1 + q \geq px_2 + pq$ 且 $px_2 \leq p(x_2 + q)$
从而 $\lfloor px_1 \rfloor + q = \lfloor px_1 + q \rfloor \geq \lfloor px_2 + pq \rfloor = \lfloor p(x_2 + q) \rfloor$ 且 $ x_1 - \lfloor px_1 \rfloor + q \geq x_2 - \lfloor px_2 \rfloor + q \geq x_2 + q - \lfloor p(x_2 + q) \rfloor$
证毕。
所以不仅我们取出的数是单调递减的，新产生的两类数值也是单调递减的。
我们可以建立三个队列 $A,B,C$，其中 $A$ 存原序列从大到小排序的结果，$B$ 存 $\lfloor px \rfloor$ 的情况，$C$ 存 $x - \lfloor px \rfloor$ 的情况。由于以上性质，最大值只可能是 $A,B,C$ 分别的队头，取出最大值然后删除对应蚯蚓，加入新的蚯蚓即可。
如果用 queue 的话可能会卡常，需要吸氧。
#pragma GCC optimize(2)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 100010, INF = 0x3f3f3f3f;
int n, m, q, u, v, t;
int a[N];
queue<int> que[4];
int main() {
scanf("%d%d%d%d%d%d", &n, &m, &q, &u, &v, &t);
for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);
sort(a + 1, a + 1 + n, [&](int a, int b) {
return a > b;
});
for (int i = 1; i <= n; i ++) que[1].push(a[i]);
for (int i = 0; i < m; i ++) {
PII maxx = max({make_pair(que[1].empty() ? -INF : que[1].front(), 1),
make_pair(que[2].empty() ? -INF : que[2].front(), 2),
make_pair(que[3].empty() ? -INF : que[3].front(), 3)});
int val = maxx.first + i * q, id = maxx.second;
que[id].pop();
int x = 1ll * val * u / v, y = val - x;
que[2].push(x - q * (i + 1)); que[3].push(y - q * (i + 1));
if (i % t == t - 1)
printf("%d ", val);
}
puts("");
for (int i = 1; i <= n + m; i ++) {
PII maxx = max({make_pair(que[1].empty() ? -INF : que[1].front(), 1),
make_pair(que[2].empty() ? -INF : que[2].front(), 2),
make_pair(que[3].empty() ? -INF : que[3].front(), 3)});
que[maxx.second].pop();
if (i % t == 0)
printf("%d ", maxx.first + q * m);
}
return 0;
}
AcWing134. 双端队列
由于最后会排成一个非降序列，所以我们不妨反向思考，将数组排序，然后尝试将数组分成尽量少的几段符合原问题。
我们记录 $A$ 为排完序后的数值，$B$ 为排完序后的下标，我们发现当 $B$ 中的一段满足先下降后上升的单谷性质时，就可以符合题意。原因是我们如果将单谷的谷点当作第一个入队，那么从谷点到谷底就相当于从队头插入，从谷底到末尾就相当于从队尾插入。
还有，如果 $A$ 中的某一段数值均相同，那么 $B$ 中的这一段就可以随意颠倒编号。因此，我们把 $A$ 分为若干段，每一段内的数值相同，然后根据 $A$ 的分段，通过改变 $B$ 的顺序，贪心地算出最小的单谷数量。具体实现并不复杂，只需要记录一下当前单谷是处于递增还是递减就可以了。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
const int N = 200010;
int n;
PII q[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i ++) {
scanf("%d", &q[i].first);
q[i].second = i;
}
sort(q + 1, q + 1 + n);
int ed = 0x3f3f3f3f, res = 1, pos = 0;
for (int i = 1; i <= n; ) {
int j = i + 1;
while (j <= n && q[j].first == q[i].first) j ++;
int l = q[i].second, r = q[j - 1].second;
if (!pos) {
if (ed > r) ed = l;
else ed = r, pos = 1;
} else {
if (ed < l) ed = r;
else ed = l, pos = 0, res ++;
}
i = j;
}
printf("%d\n", res);
return 0;
}
单调队列
AcWing154. 滑动窗口
单调队列模板题。
先简略的讲一下单调队列。如果有一个旧的数，并且比新来的数大，那么旧的数一定不可能成为最小值，所以可以不考虑旧的数。所以我们可以用一个队列来维护，每插入一个数就从队末开始把所有被单调队列的数删掉，然后再从队头开始把所有与当前数值下标差距大于 $m$ 的数删掉，最后把新的数加入队尾。
为了方便处理，单调队列中存的都是下标。
以上所述都是维护最小值的单调队列，或用一下就是维护最大值。
#include <iostream>
using namespace std;
const int N = 1000010;
int n, m, a[N], q[N], hh, tt = -1;
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);
for (int i = 1; i <= n; i ++) {
while (hh <= tt && a[q[tt]] >= a[i]) tt --;
while (hh <= tt && i - q[hh] >= m) hh ++;
q[++ tt] = i;
if (i >= m) printf("%d ", a[q[hh]]);
}
puts("");
hh = 0, tt = -1;
for (int i = 1; i <= n; i ++) {
while (hh <= tt && a[q[tt]] <= a[i]) tt --;
while (hh <= tt && i - q[hh] >= m) hh ++;
q[++ tt] = i;
if (i >= m) printf("%d ", a[q[hh]]);
}
return 0;
}
AcWing135. 最大子序和
先求出前缀和数组，然后我们发现对于 $s_r$ 来说一定要找到最小的 $s_{l - 1}$，然后就算 $s_r - s_{l - 1}$。这可以用单调队列维护。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 300010;
LL n, m;
LL q[N], hh, tt = -1, s[N];
int main() {
LL res = INT_MIN, maxx;
cin >> n >> m;
for (int i = 1; i <= n; i ++) {
LL x; cin >> x;
s[i] = s[i - 1] + x;
res = max(res, x);
}
maxx = res;
q[++ tt] = 0;
for (int i = 1; i <= n; i ++) {
while (hh <= tt && i - q[hh] > m) hh ++;
while (hh <= tt && s[i] <= s[q[tt]]) tt --;
q[++ tt] = i;
res = max(res, s[i] - s[q[hh]]);
}
printf("%lld\n", res == 0 ? maxx : res);
return 0;
}
0x13 链表
AcWing136. 邻值查找
很经典的思路，先把 $A$ 排序，在排序的过程中记录 $B$，表示原始序列中的 $A_i$ 现在处于哪个位置。然后从 $n$ 开始，找到 $B_n$ 所对应的链表节点，答案一定是该节点的左结点或右结点，最后把这个结点删掉。按照此种做法，我们可以接着找出 $n - 1, n - 2, …, 2$ 的答案。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef pair<LL, int> PII;
const int N = 100010;
int n, p[N], l[N], r[N];
PII a[N], ans[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i ++) {
scanf("%lld", &a[i].first);
a[i].second = i;
}
sort(a + 1, a + 1 + n);
a[0].first = -3000000100, a[n + 1].first = 3000000100;
for (int i = 1; i <= n; i ++) {
l[i] = i - 1, r[i] = i + 1;
p[a[i].second] = i;
}
for (int i = n; i >= 2; i --) {
int j = p[i], pre = l[j], ne = r[j];
LL pv = abs(a[j].first - a[pre].first), nv = abs(a[j].first - a[ne].first);
if (pv > nv) {
ans[i] = {nv, a[ne].second};
} else {
ans[i] = {pv, a[pre].second};
}
l[ne] = pre, r[pre] = ne;
}
for (int i = 2; i <= n; i ++)
printf("%lld %lld\n", ans[i].first, ans[i].second);
return 0;
}
0x14 哈希
哈希函数设计
AcWing137. 雪花雪花雪花
考虑设计哈希函数 $H(i) = (\sum^{6}_{j = 1}a_{i, j} + \prod^{6}_{j = 1}a_{i, j}) \% P$，然后对于每一片雪花在哈希表中存所有可能的哈希值即可。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010, P = 99991;
int T, a[N];
int e[N][6], ne[N], h[N], idx;
int H(int *a) {
int sum = 0, mul = 1;
for (int i = 0; i < 6; i ++) {
sum = (sum + a[i]) % P;
mul = (LL)mul * a[i] % P;
}
return (sum + mul) % P;
}
bool equal(int *a, int *b) {
for (int i = 0; i < 6; i ++)
for (int j = 0; j < 6; j ++) {
int f = true;
for (int k = 0; k < 6; k ++)
if (a[(i + k) % 6] != b[(j + k) % 6])
f = false;
if (f) return f;
f = true;
for (int k = 0; k < 6; k ++)
if (a[(i + k) % 6] != b[(j - k + 6) % 6])
f = false;
if (f) return f;
}
return false;
}
bool insert(int *a) {
int hash = H(a);
for (int i = h[hash]; ~i; i = ne[i])
if (equal(e[i], a)) return true;
memcpy(e[idx], a, sizeof e[idx]);
ne[idx] = h[hash];
h[hash] = idx ++;
return false;
}
int main() {
memset(h, -1, sizeof h);
scanf("%d", &T);
bool f = false;
while (T --) {
for (int i = 0; i < 6; i ++) scanf("%d", &a[i]);
if (insert(a)) f = true;
}
if (f) puts("Twin snowflakes found.");
else puts("No two snowflakes are alike.");
return 0;
}
字符串哈希
AcWing138. 兔子与兔子
字符串哈希模板题。字符串哈希原理就不写了。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef unsigned long long ULL;
const int N = 1000010, P = 13331;
int n;
ULL s[N], p[N];
string str;
ULL get(int l, int r) {
return s[r] - s[l - 1] * p[r - l + 1];
}
int main() {
cin >> str;
scanf("%d", &n);
int m = str.size(); str = ' ' + str;
p[0] = 1;
for (int i = 1; i <= m; i ++) {
p[i] = p[i - 1] * P;
s[i] = s[i - 1] * P + str[i];
}
while (n --) {
int l1, r1, l2, r2;
scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
if (get(l1, r1) == get(l2, r2)) {
puts("Yes");
} else {
puts("No");
}
}
return 0;
}
AcWing139. 回文子串的最大长度
首先对于一个长度为 $n$ 的回文串，令 $mid = \frac{n + 1}{2}$ ，如果 $n$ 是奇数，那么 $S[1$ ~ $mid - 1] = S[n$ ~ $mid + 1]$，如果 $n$ 是偶数，那么 $S[1$ ~ $mid] = S[mid + 1$ ~ $n]$。所以我们可以顺着和倒着分别求一次字符串哈希来判断。
为了方便处理，我们可以在每两个字符之间加一个 #，这样一个偶数长度的字符串就变成了奇数长度。
我们先枚举一遍 $i$，然后考虑二分以 $i$ 为中点的回文串的长度，用字符串哈希进行判断即可。
一个值得注意的细节是，回文串的长度会因为 $s_{i - l}$ 是否为 # 进行改变，需要画一个图研究。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef unsigned long long ULL;
const int N = 2000010, P = 13331;
ULL p[N], h1[N], h2[N];
char str[N];
int Case;
ULL get(ULL *h, int l, int r) {
return h[r] - h[l - 1] * p[r - l + 1];
}
void solve() {
int n = strlen(str + 1);
for (int i = n * 2; i > 0; i -= 2) {
str[i] = str[i / 2];
str[i - 1] = 'z' + 1;
}
n *= 2;
p[0] = 1;
for (int i = 1, j = n; i <= n; i ++, j --) {
p[i] = p[i - 1] * P;
h1[i] = h1[i - 1] * P + str[i];
h2[i] = h2[i - 1] * P + str[j];
}
int res = 0;
for (int i = 1; i <= n; i ++) {
int l = 0, r = min(i - 1, n - i);
while (l < r) {
int mid = l + r + 1 >> 1;
if (get(h1, i - mid, i - 1) != get(h2, n - (i + mid) + 1, n - i)) r = mid - 1;
else l = mid;
}
if (str[i - l] <= 'z') res = max(res, l + 1);
else res = max(res, l);
}
printf("Case %d: %d\n", ++ Case, res);
}
int main() {
while (scanf("%s", str + 1) == 1 && strcmp(str + 1, "END")) solve();
return 0;
}
AcWing140. 后缀数组
首先，考虑 $Height$ 数组的求法，对于两个后缀求最长公共前缀，我们可以用字符串哈希加上二分，具体的，如果当前 $a_1, a_2, …, a_{mid}$ 的哈希值不等于 $b_1, b_2, …, b_{mid}$ 的哈希值，那么说明答案在 $mid$ 的左侧，$r = mid - 1$，否则 $l = mid$。
如何快速求出 $Ranks_i$ 呢？直接排序显然每次比较操作是 $O(N)$ 的，总和 $O(N^2logN)$ 无法通过。但是我们可以通过上述类似操作，在比较两个后缀 $A$ 和 $B$ 字典序时，先找出它们的最长公共前缀 $x$，再比较 $A_{x + 1}$ 和 $B_{x + 1}$ 的大小关系即可。注意，如果一个后缀是另一个后缀的前缀，那么这个后缀一定比另一个后缀字典序小。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef unsigned long long ULL;
const int N = 300010, INF = 0x3f3f3f3f, P = 13331;
int n, ranks[N];
char s[N];
ULL h[N], p[N];
void init() {
p[0] = 1;
for (int i = 1; i <= n; i ++) {
p[i] = p[i - 1] * P;
h[i] = h[i - 1] * P + s[i];
ranks[i] = i;
}
}
ULL get(int l, int r) {
return h[r] - h[l - 1] * p[r - l + 1];
}
int calc(int a, int b) {
int l = 0, r = min(n - a + 1, n - b + 1);
while (l < r) {
int mid = l + r + 1 >> 1;
if (get(a, a + mid - 1) != get(b, b + mid - 1)) r = mid - 1;
else l = mid;
}
return l;
}
bool cmp(int a, int b) {
int l = calc(a, b);
int v1 = a + l > n ? -INF : s[a + l];
int v2 = b + l > n ? -INF : s[b + l];
return v1 < v2;
}
int main() {
scanf("%s", s + 1);
n = strlen(s + 1);
init();
sort(ranks + 1, ranks + 1 + n, cmp);
for (int i = 1; i <= n; i ++) printf("%d ", ranks[i] - 1);
puts("");
for (int i = 1; i <= n; i ++)
if (i == 1) printf("0 ");
else printf("%d ", calc(ranks[i - 1], ranks[i]));
return 0;
}
二维哈希
AcWing156. 矩阵
首先对每一行求出行内哈希值，接着考虑如果当前已知第 $i - a$ 到 $i - 1$ 行的哈希值如何推出第 $i - a + 1$ 到第 $i$ 行的哈希值。首先假设第 $i - 1$ 行的哈希值为 $S_{i - 1}$，$H(k, l, r)$ 表示第 $k$ 行从 $l$ 到 $r$ 的哈希值。那么 $S_i = S_{i - 1} \times p^b + H(i, l, r) - H(i - a) \times p^{a+b}$
理解一下这个式子，首先 $S_{i - 1} \times p^b$ 相当于将原矩阵下移了一行，$+H(i,l,r)$ 就是加上我们 $i$ 的这一行，后面减去的那一坨因为我们下移一行在加上第 $i$ 行的同时也要把第 $i - a$ 行删掉，后面乘上 $p^{a + b}$ 是因为我们和一位字符串哈希一样，要把删去的部分和最高位对齐，所以要先乘 $p^b$ 再乘 $p^a$。
做这个问题的关键是把一个 $a\times b$ 的矩阵变成长度为 $a\times b$ 的数组进行哈希，理解了这一点这些乘方就很清晰了。
然后我们把所有的子矩阵的哈希值扔进哈希表里，查询访问即可。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_set>
using namespace std;
typedef unsigned long long ULL;
const int N = 1010, P = 13331;
int n, m, a, b, q;
char str[N];
ULL h[N][N], p[N * N];
ULL get(ULL f[], int l, int r) {
return f[r] - f[l - 1] * p[r - l + 1];
}
int main() {
scanf("%d%d%d%d", &m, &n, &a, &b);
p[0] = 1;
for (int i = 1; i <= n * m; i ++) p[i] = p[i - 1] * P;
for (int i = 1; i <= n; i ++) {
scanf("%s", str + 1);
for (int j = 1; j <= m; j ++) h[i][j] = h[i][j - 1] * P + str[j] - '0';
}
unordered_set<ULL> S;
for (int i = b; i <= m; i ++) {
int l = i - b + 1, r = i;
ULL s = 0;
for (int j = 1; j <= n; j ++) {
s = s * p[b] + get(h[j], l, r);
if (j > a) s -= get(h[j - a], l, r) * p[a * b];
if (j >= a) S.insert(s);
}
}
scanf("%d", &q);
while (q --) {
ULL s = 0;
for (int i = 1; i <= a; i ++) {
scanf("%s", str + 1);
for (int j = 1; j <= b; j ++) s = s * P + str[j] - '0';
}
if (S.count(s)) puts("1");
else puts("0");
}
return 0;
}
0x15 KMP
循环类问题
AcWing141. 周期
引理：$S[1$ ~ $i]$ 具有长度为 $len$ 的循环节的充要条件是 $len | i$ 且 $S[1$ ~ $i -len] = S[len + 1$ ~ $ i]$，即长度为 $len$ 的前缀等于后缀。
证明：
必要性：由于 $S[1 \sim i -len]$ 和 $S[len + 1\sim i]$ 一定都是由 $i \div len - 1$ 个循环元组成的，相等。
充分性： 一个显然的事情是 $S[i \sim len] = S[len + 1 \sim 2 \times len]$，所以 $S[1 \sim i - len] = S[len + 1 \sim i]$，即 $S[1 \sim i - len]$ 与 $S[len+1 \sim i]$ 是错位对齐的。
由于引理的存在，我们便得到了最小循环节长度就是 $i - next[i]$，原因是 $next[i]$ 由引理有一个候选项 $i - len$。那么最大循环次数就是 $i \div (i - next[i])$，前提是 $i - next[i] \ | \ i$ 。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000010;
int n, ne[N], Case;
char s[N];
void solve() {
for (int i = 2, j = 0; i <= n; i ++) {
while (j && s[i] != s[j + 1]) j = ne[j];
if (s[i] == s[j + 1]) j ++;
ne[i] = j;
}
printf("Test case #%d\n", ++ Case);
for (int i = 1; i <= n; i ++)
if (i != i - ne[i] && i % (i - ne[i]) == 0)
printf("%d %d\n", i, i / (i - ne[i]));
puts("");
}
int main() {
while (scanf("%d", &n) == 1 && n) {
scanf("%s", s + 1);
solve();
}
return 0;
}
AcWing159. 奶牛矩阵
先暴力找出每一行的循环节长度，然后找出所有行公共的循环节长度的最小值 $w$，接着将每一行的 $1 \sim w$ 视为一个整体按列跑一遍 $KMP$，找到最小的高 $h = n - next[n]$，$w \times h$ 即为最小面积。
为什么要找出最小值 $w$ 呢？我们可以发现如果有 $w_1 > w$，那么 $w_1$ 在进行列的 $KMP$ 时 $next$ 一定更小，所以 $n - next$ 就会更大，即 $w_1$ 匹配出来的 $h$ 一定大于 $w$ 匹配出来的 $h$，所以 $w$ 一定优于 $w_1$。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10010, M = 80;
int n, m, ne[N];
bool st[N];
char str[N][M];
int main() {
memset(st, true, sizeof st);
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++) {
scanf("%s", str[i]);
for (int j = 1; j <= m; j ++)
if (st[j])
for (int k = j; k < m; k += j) {
for (int u = 0; u < j && u + k < m; u ++)
if (str[i][u] != str[i][u + k]) {
st[j] = false;
break;
}
if (!st[j]) break;
}
}
int w = 0;
for (int i = 1; i <= m; i ++)
if (st[i]) {
w = i;
break;
}
for (int i = 2, j = 0; i <= n; i ++) {
while (j && strcmp(str[i], str[j + 1])) j = ne[j];
if (!strcmp(str[i], str[j + 1])) j ++;
ne[i] = j;
}
printf("%d\n", w * (n - ne[n]));
return 0;
}
KMP 的灵活运用
160. 匹配统计 - AcWing题库
我们考虑用 $f[i]$ 表示匹配长度至少为 $i$ 的数量，那么恰好为 $i$ 的数量就应该是 $f[i] - f[i + 1]$。
如果暴力计算 $f[i]$ 的话就要每次让 $f[ne[j]], f[ne[ne[j]]], …$ 都加 $1$，这显然不可取。我们发现每次 $f[i]$ 加的时候，$f[ne[j]]$ 一定会加，所以我们只需要让 $f[ne[j]] += f[j]$ 就行了，不用每次枚举。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 200010;
int n, m, q;
int ne[N], f[N];
char a[N], b[N];
int main() {
cin >> n >> m >> q;
cin >> a + 1 >> b + 1;
for (int i = 2, j = 0; i <= m; i ++) {
while (j && b[i] != b[j + 1]) j = ne[j];
if (b[i] == b[j + 1]) j ++;
ne[i] = j;
}
for (int i = 1, j = 0; i <= n; i ++) {
while (j && a[i] != b[j + 1]) j = ne[j];
if (a[i] == b[j + 1]) j ++;
f[j] ++;
}
for (int i = m; i >= 1; i --)
f[ne[i]] += f[i];
while (q --) {
int x; cin >> x;
cout << f[x] - f[x + 1] << endl;
}
return 0;
}
字符串最小表示法
先简单说下最小表示法。
先把字符串复制一份接在末尾，然后令 $b[i]$ 表示 $S[i \sim i+n-1]$。
引理：对于所有 $B[i], B[j]$ 且存在 $S[i + k] > S[j + k]$，那么 $B[i], B[i + 1], …, B[i + k]$ 都不会是最小表示。
这个引理的正确性是显然的，假设 $i \leq u \leq k$，那么对于 $B[i + u]$ 我们一定有 $B[j + u]$ 比 $B[i+u]$ 更小。
所以我们可以在匹配开始时令 $i = 2, j = 0$，然后不断往后匹配，直到找到 $S[i + k] != S[j + k]$，然后比较大小，确定是 $i = i + k + 1$ 或者 $j = j +k + 1$。
AcWing158. 项链
分别求出两个字符串的最小表示然后比较是否相等即可。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000010;
int n;
char a[N], b[N];
int calc(char s[]) {
int i = 1, j = 2;
while (i <= n && j <= n) {
int k = 0;
while (s[i + k] == s[j + k]) k ++;
if (k == n) break;
if (s[i + k] < s[j + k]) j = j + k + 1;
else i = i + k + 1;
if (i == j) i ++;
}
s[min(i, j) + n] = '\0';
return min(i, j);
}
int main() {
scanf("%s%s", a + 1, b + 1);
n = strlen(a + 1);
memcpy(a + 1 + n, a + 1, n);
memcpy(b + 1 + n, b + 1, n);
int pa = calc(a), pb = calc(b);
if (!strcmp(a + pa, b + pb)) {
puts("Yes");
printf("%s\n", a + pa);
} else {
puts("No");
}
return 0;
}
树的最小表示法
AcWing157. 树形地铁系统
树的最小表示法比较奇特，我们可以把一个节点的所有子树排序，递归地做就一定能求出树的最小表示。
为了方便处理我们可以制造一个虚根，即在字符串开头加一个 $0$，末尾加一个 $1$。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
int T;
string dfs(string seq, int &u) {
u ++;
vector<string> seqs;
while (seq[u] == '0') seqs.push_back(dfs(seq, u));
u ++;
sort(seqs.begin(), seqs.end());
string res = "0";
for (auto c : seqs) res += c;
res += '1';
return res;
}
int main() {
cin >> T;
while (T --) {
string a, b;
cin >> a >> b;
a = '0' + a + '1';
b = '0' + b + '1';
int ua = 0, ub = 0;
if (dfs(a, ua) == dfs(b, ub)) puts("same");
else puts("different");
}
return 0;
}
0x16 Trie
Trie 的简单运用
AcWing142. 前缀统计
超级模板题，不会左转出门基础课。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int n, m, idx;
int trie[N][26], ed[N];
char s[N];
void insert(char s[]) {
int l = strlen(s + 1), p = 0;
for (int i = 1; i <= l; i ++) {
int c = s[i] - 'a';
if (!trie[p][c]) trie[p][c] = ++ idx;
p = trie[p][c];
}
ed[p] ++;
}
int query(char s[]) {
int l = strlen(s + 1), p = 0, res = 0;
for (int i = 1; i <= l; i ++) {
int c = s[i] - 'a';
p = trie[p][c];
if (p == 0) return res;
res += ed[p];
}
return res;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++) {
scanf("%s", s + 1);
insert(s);
}
while (m --) {
scanf("%s", s + 1);
int res = query(s);
printf("%d\n", res);
}
return 0;
}
AcWing161. 电话列表
在插入的时候就判断是否包含别的字符串或者是否被别的字符串包含。
具体我们可以在插入的时候统计一个 $cnt$ 代表我们插入时经历了几次 $trie[p][c] != 0$，如果为 $|S|$ 次，就说明 $S$ 是其它字符串的前缀。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000010;
int T, n, idx, trie[N][11];
bool ed[N];
string s[N];
bool insert(string s) {
int n = s.size(), p = 0, cnt = 0;
bool f = true;
for (int i = 0; i < n; i ++) {
int c = s[i] - '0';
if (!trie[p][c]) trie[p][c] = ++ idx;
else cnt ++;
if (ed[p]) f = false;
p = trie[p][c];
}
ed[p] = true;
if (cnt == n) f = false;
return f;
}
int main() {
scanf("%d", &T);
while (T --) {
idx = 0;
memset(ed, false, sizeof ed);
memset(trie, 0, sizeof trie);
scanf("%d", &n);
bool f = true;
for (int i = 1; i <= n; i ++) {
cin >> s[i];
if (!insert(s[i])) f = false;
}
if (!f) puts("NO");
else puts("YES");
}
return 0;
}
Trie 与异或
AcWing143. 最大异或对
我们把每个整数的二进制位从高到低插入 trie 中。由于异或不同为 $1$，相同为 $0$，所以我们在查询的时候从高到低枚举每一位，如果该位是 $u$，就查找是否存在 $!u$，否则选择 $u$。
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, trie[N * 31][2],idx, a[N];
void insert(int x) {
int p = 0;
for (int i = 30; i >= 0; i --) {
int c = x >> i & 1;
if (!trie[p][c]) trie[p][c] = ++ idx;
p = trie[p][c];
}
}
int query(int x) {
int p = 0, res = 0;
for (int i = 30; i >= 0; i --) {
int c = x >> i & 1;
if (trie[p][!c]) {
res = res * 2 + !c;
p = trie[p][!c];
} else {
res = res * 2 + c;
p = trie[p][c];
}
}
return res;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i ++) {
scanf("%d", &a[i]);
insert(a[i]);
}
int ans = -1;
for (int i = 1; i <= n; i ++)
ans = max(ans, a[i] ^ query(a[i]));
printf("%d\n", ans);
return 0;
}
AcWing144. 最长异或值路径
我们求出 $d[i]$ 表示从根节点到 $i$ 的异或值。那么 $i$ 到 $j$ 的异或距离就应该是 $d[i] \oplus d[j]$，因为 $i$ 到根节点和 $j$ 到根节点一定是有重叠的部分，而重叠的部分异或值为 $0$，所以 $d[i] \oplus d[j]$ 就是我们的答案。
我们只要像上一题一样把 $d$ 全部存到 trie 里就行了。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int e[N], w[N], ne[N], h[N], idx;
int trie[N * 31][2], tot;
int d[N], in[N], rt;
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
void insert(int x) {
int p = 0;
for (int i = 30; i >= 0; i --) {
int u = x >> i & 1;
if (!trie[p][u]) trie[p][u] = ++ tot;
p = trie[p][u];
}
}
int query(int x) {
int p = 0, res = 0;
for (int i = 30; i >= 0; i --) {
int u = x >> i & 1;
if (trie[p][!u]) {
res = res * 2 + !u;
p = trie[p][!u];
} else {
res = res * 2 + u;
p = trie[p][u];
}
}
return res;
}
void dfs(int u) {
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i], k = w[i];
d[j] = d[u] ^ k;
dfs(j);
}
}
int main() {
memset(h, -1, sizeof h);
scanf("%d", &n);
for (int i = 1; i < n; i ++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
in[b] ++;
}
for (int i = 0; i < n; i ++)
if (!in[i]) rt = i;
dfs(rt);
int ans = 0;
for (int i = 0; i < n; i ++) {
insert(d[i]);
int s = query(d[i]);
ans = max(ans, d[i] ^ s);
}
printf("%d\n", ans);
return 0;
}
0x17 堆
堆的运用
AcWing145. 超市
我们考虑贪心，先把所有物品按照过期时间排序。假设当前取的物品过期时间为 $i$，那么如果我们已经取了 $i$ 个物品，那我们就应该用当前物品去替换已选择的利润最小的物品；如果我们还没取 $i$ 个物品，我们就直接将 $i$ 选上。利润最小的物品可以用堆来维护。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 10010;
int n;
PII q[N];
int main() {
while (scanf("%d", &n) == 1) {
for (int i = 1; i <= n; i ++)
scanf("%d%d", &q[i].first, &q[i].second);
sort(q + 1, q + 1 + n, [&](PII a, PII b) {
return a.second < b.second;
});
priority_queue<PII, vector<PII>, greater<PII>> heap;
for (int i = 1; i <= n; i ++) {
if (q[i].second > heap.size()) heap.push(q[i]);
else if (q[i].second == heap.size() && heap.top().first < q[i].first) {
heap.pop();
heap.push(q[i]);
}
}
int res = 0;
while (heap.size()) {
res += heap.top().first;
heap.pop();
}
printf("%d\n", res);
}
return 0;
}
AcWing146. 序列
我们先考虑如何从 $A$ 和 $B$ 两个序列中推出最小的 $n$ 个值。
我们把 $A$ 排序后根据 $B$ 分组，如下：
$ \left\{\begin{matrix} A_1 + B_1, A_2 + B_1, …, A_n + B_1 & \\ A_1 + B_2, A_2 + B_2, …, A_n + B_2 & \\ … &\\ A_1 + B_n, A_2 + B_n, …, A_n + B_n & \end{matrix}\right.$
我们可以把第一列的所有数插入堆，那么最小值就应该是堆顶。我们取出堆顶后把堆顶数的下一位加入堆，即如果当前最小值是 $A_i + B_j$，那我们把 $A_i + B_j$ 取出，然后把 $A_{i+1} + B_j$ 再次存入堆。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 2010;
int T, n, m, w[N][N], sz, t[N];
struct node {
int x, y, k;
} h[N];
void down(int u) {
int p = u * 2;
while (p <= sz) {
if (p < sz && h[p].k > h[p + 1].k) p ++;
if (h[u].k > h[p].k) swap(h[u], h[p]), u = p, p *= 2;
else break;
}
}
void up(int u) {
while (u / 2 && h[u / 2].k > h[u].k)
swap(h[u / 2], h[u]), u /= 2;
}
void remove() {
h[1] = h[sz --];
down(1);
}
void work(int x) {
sort(w[x] + 1, w[x] + 1 + m);
sz = 0;
for (int i = 1; i <= m; i ++) {
h[++ sz] = {1, i, w[x][1] + w[x + 1][i]};
up(sz);
}
int cnt = 0;
for (int k = 1; k <= m; k ++) {
node top = h[1];
t[++ cnt] = h[1].k;
remove();
h[++ sz] = {top.x + 1, top.y, w[x][top.x + 1] + w[x + 1][top.y]};
up(sz);
}
memcpy(w[x + 1], t, sizeof w[x + 1]);
}
int main() {
scanf("%d", &T);
while (T --) {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++)
scanf("%d", &w[i][j]);
if (n == 1) {
sort(w[1] + 1, w[1] + 1 + m);
} else {
for (int i = 1; i < n; i ++)
work(i);
}
for (int i = 1; i <= m; i ++) printf("%d ", w[n][i]);
puts("");
}
return 0;
}
AcWing147. 数据备份
首先我们可以发现我们每次只可能选相邻的两个办公楼，这个是显然的。所以我们可以令 $D_i = A_i - A_{i - 1}$。
引理：对于最小值 $D_i$，两边的 $D_{i - 1}$ 和 $D_{i + 1}$ 要么都选要么都不选。
证明：如果选择了 $D_{i - 1}$ 和一个很远的 $D_j$，那肯定就不如选 $D_j$ 和 $D_i$，因为 $D_i$ 是最小值。所以 $D_{i - 1}$ 和 $D_{i + 1}$ 要么都选，要么都不选。
因此，我们可以用一个链表存 $D$ 数组，然后用一个 $set$ 存 $D$ 的最小值。每次取出 $D$ 的最小值 $D_i$，然后将 $D_{i - 1}$ 和 $D_{i + 1}$ 从链表和 $set$ 中删去，把 $D_i$ 的改为 $D_{i - 1} + D_{i + 1} - D_i$，这样如果后来我们又选了 $D_{i - 1} + D_{i + 1} - D_i$，那么相当于只选了 $D_{i - 1} + D_{i + 1}$。
至此，我们巧妙地做完了这道题。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <set>
using namespace std;
typedef long long LL;
typedef pair<LL, int> PLI;
const int N = 100010, INF = 0x3f3f3f3f;
int n, k;
int l[N], r[N];
LL d[N];
void remove(int p) {
l[r[p]] = l[p];
r[l[p]] = r[p];
}
int main() {
scanf("%d%d", &n, &k);
for (int i = 0; i < n; i ++) scanf("%lld", &d[i]);
for (int i = n - 1; ~i; i --) d[i] -= d[i - 1];
d[0] = d[n] = INF;
set<PLI> h;
for (int i = 1; i < n; i ++) {
l[i] = i - 1, r[i] = i + 1;
h.insert({d[i], i});
}
LL res = 0;
while (k --) {
auto it = h.begin();
LL v = it->first;
int pos = it->second, left = l[pos], right = r[pos];
remove(left); remove(right);
res += v;
h.erase(it);
h.erase({d[left], left}); h.erase({d[right], right});
h.insert({d[left] + d[right] - v, pos});
d[pos] = d[left] + d[right] - v;
}
printf("%lld\n", res);
return 0;
}
AcWing163. 生日礼物
PS：这段写的有点不清不楚的，后面再改表述。
我们可以把 $A$ 数组分成连续的正数段和负数段，然后记正数段的个数为 $cnt$，如果 $cnt \leq m$，那直接全选上就可以了。如果 $cnt > m$，那就要删掉 $cnt - m$ 段。我们考虑如何删除最优。
令所有正段的和为 $S$，我们有两种选择：
- 删除一段正段（$S - a_i$）
- 将 $k$ 段正段与 $k - 1$ 段负段合并起来 （$S - |a_i| - …$，其中 $a_i$ 为负段的和）
这样我们的问题就与上一题等价了。
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 100010;
int n, m;
int a[N], l[N], r[N];
bool st[N];
priority_queue<PII, vector<PII>, greater<PII>> q;
void del(int p) {
r[l[p]] = r[p];
l[r[p]] = l[p];
st[p] = true;
}
int main() {
scanf("%d%d", &n, &m);
int k = 0;
for (int i = 1; i <= n; i ++) {
int x; scanf("%d", &x);
if (!x) continue;
if (!k || (long long)a[k] * x < 0) a[++ k] = x;
else a[k] += x;
}
int res = 0, cnt = 0;
for (int i = 1; i <= k; i ++) {
q.push({abs(a[i]), i});
l[i] = i - 1, r[i] = i + 1;
if (a[i] > 0) res += a[i], cnt ++;
}
while (cnt > m) {
while (st[q.top().second]) q.pop();
auto t = q.top();
q.pop();
int v = t.first, p = t.second;
int left = l[p], right = r[p];
if (left != 0 && right != k + 1 || a[p] > 0) {
cnt --;
res -= v;
a[p] += a[left] + a[right];
q.push({abs(a[p]), p});
del(left); del(right);
}
}
printf("%d\n", res);
return 0;
}
对顶堆
AcWing162. 黑盒子
考虑对顶堆，由于已经有一个 $u$ 数组告诉我们长度，所以我们假设当前考虑 $1 \sim u_i$，那么我们可以用一个大根堆存前 $i$ 小的数，一个小根堆存其它的数，进行维护即可。
当然，每次 $i + 1$ 的时候都要将小根堆队头元素插入大根堆。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 30010;
int n, m;
int a[N], p[N];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++) cin >> a[i];
for (int i = 1; i <= m; i ++) cin >> p[i];
int i = 1;
priority_queue<int> l;
priority_queue<int, vector<int>, greater<int>> r;
for (int k = 1; k <= m; k ++) {
while (l.size() < k && r.size()) {
l.push(r.top());
r.pop();
}
int len = p[k];
for(; i <= len; i ++) {
if (l.size() < k) l.push(a[i]);
else {
if (l.top() < a[i]) r.push(a[i]);
else {
r.push(l.top());
l.pop();
l.push(a[i]);
}
}
}
printf("%d\n", l.top());
}
return 0;
}
哈夫曼树
$k$ 叉哈夫曼树即构造一棵包含 $n$ 个叶子结点的 $k$ 叉树，令第 $i$ 个点的权值为 $w_i$，到根节点的距离为 $l_i$，最小化 $\sum w_i\times l_i$。
对于 $k=2$ 的情况，我们容易想到贪心的算法，用一个小根堆存 $w$，每次从堆中取出最小值和次小值 $w_1, w_2$，再从堆中删掉它们。然后将答案加上 $w_1 + w_2$，再把 $w_1 + w_2$ 加入小根堆中。
考虑将这个贪心算法扩展到 $k>2$ 的情况。此时我们不能简单地改为每次从堆中取出最小的 $k$ 个权值，因为如果最后一轮循环时堆中不足以取出 $k$ 个数，整个根的子节点个数就会小于 $k$，就不对了。所以我们可以在执行上述贪心算法时加入一些额外的 $0$，使得 $(n - 1)\ mod\ (k - 1) = 0$。
AcWing148. 合并果子
简单地二叉哈夫曼树问题。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 10010;
int n, a[N];
int main() {
priority_queue<int, vector<int>, greater<int>> q;
cin >> n;
for (int i = 1; i <= n; i ++) {
cin >> a[i];
q.push(a[i]);
}
long long res = 0, sum;
for (int i = 1; i < n; i ++) {
sum = q.top();
q.pop();
sum += q.top();
q.pop();
q.push(sum);
res += sum;
}
cout << res << endl;
return 0;
}
其实还有一种 $O(n)$ 做法可以不用堆。我们发现 $A$ 的数值很小，所以可以先把 $A$ 的数值桶排，然后把 $A$ 中的数值加入 $q1$，而计算过程中新加入的值放入 $q2$。仔细想想可以发现 $q2$ 是单调的，这样每次的最小值一定是 $q1$ 和 $q2$ 的队头，所以我们不需要使用堆，只需要最简单的队列即可完成。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
typedef long long LL;
const int N = 10000010;
int n, a[N], b[N];
queue<LL> q1, q2;
inline LL read() {
LL x = 0, f = 1;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch)) {
x = (x << 1) + (x << 3) + (ch ^ 48);
ch = getchar();
}
return x * f;
}
inline void write(LL x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
LL add() {
LL x;
if (q2.empty() || !q1.empty() && q1.front() < q2.front()) {
x = q1.front();
q1.pop();
} else {
x = q2.front();
q2.pop();
}
return x;
}
int main() {
n = read();
for (int i = 1; i <= n; i ++) {
a[i] = read();
b[a[i]] ++;
}
for (int i = 1; i <= 100000; i ++)
while (b[i] --) q1.push(i);
LL res = 0, sum;
for (int i = 1; i < n; i ++) {
LL b = add(), c = add();
q2.push(b + c);
res += b + c;
}
write(res);
return 0;
}
AcWing149. 荷马史诗
题目中所要求的编码实际上就是哈夫曼编码，所以这其实是一个 $k$ 叉哈夫曼树问题。题目中要求最长字符串长度最短，我们只需要记录每个结点和其它结点合并的次数，每次合并时优先选择合并次数最少得结点即可。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
typedef long long LL;
typedef pair<LL, int> PLI;
const int N = 100010;
int n, k;
LL w[N];
priority_queue<PLI, vector<PLI>, greater<PLI>> q;
int main() {
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i ++) scanf("%lld", &w[i]);
while ((n - 1) % (k - 1)) w[++ n] = 0;
for (int i = 1; i <= n; i ++) q.push({w[i], 0});
LL res = 0, dep = 0;
while (q.size() > 1) {
LL sum = 0;
for (int i = 1; i <= k; i ++) {
auto t = q.top(); q.pop();
sum += t.first;
dep = max(dep, (LL)t.second + 1);
}
q.push({sum, dep});
res += sum;
}
printf("%lld\n%lld\n", res, q.top().second);
return 0;
}
完结撒花✿✿ヽ(°▽°)ノ✿~~
2024/11/25 18:29 已完结