https://oi-wiki.org/ds/li-chao-tree/

要求在平面直角坐标系下维护两个操作：
1.在平面上加入一条线段。记第$i$条被插入的线段的标号为$i$。
2.给定一个数$k$,询问与直线$x=k$相交的线段中，交点纵坐标最大的线段的编号。

区间修改要想到懒标记，那么这里懒标记可以是线段的编号。如果某个区间在被线段包裹，且本身没有标记，则可以直接打上标记。但是如果本身有标记，除了要更新自己，而且由于线段是斜的，懒标记还需要递归下传。我们如下考虑下传：

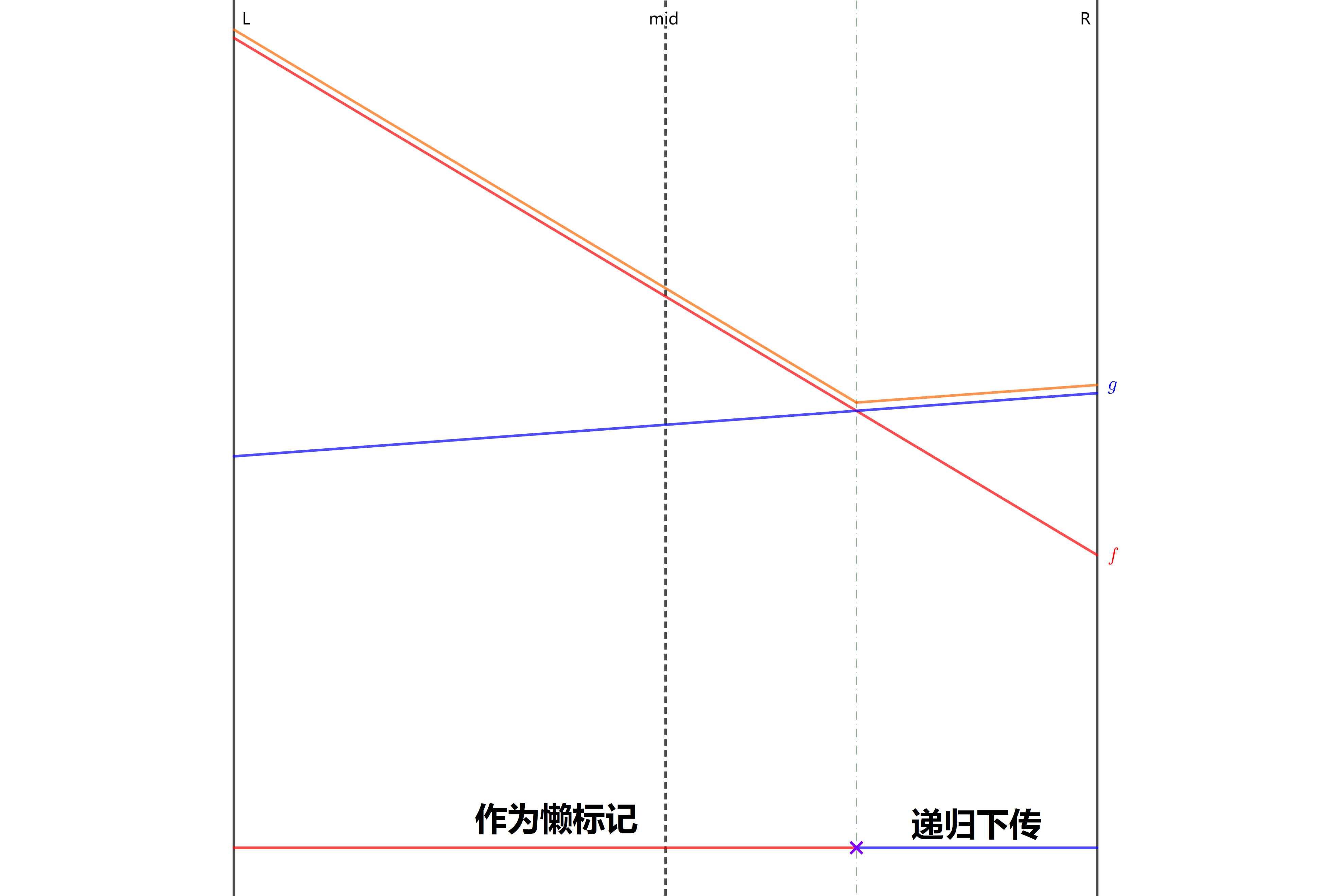
如果要修改懒标记，两个线段一定交于一点，其中肯定有一个子区间被左区间或右区间完全包含，也就是说，在两条线段中，肯定有一条线段，只可能成为左区间的答案，或者只可能成为右区间的答案。我们用这条线段递归更新对应子树，用另一条线段作为懒标记更新整个区间，这就保证了递归下传的复杂度。（懒标记只会下传到某个子儿子）

线段树节点维护该区间中点处最高的线段
设新线段是f,旧懒标记线段是g。
1.简化分析，如果中点处f优于g，则交换。只考虑中点处f不如g的情况
2.如果左端点f更优，说明交点在左区间，懒标记递归到左儿子中下传
3.如果右端点f更优，说明交点在右区间，懒标记递归到右边下传
4.如果都不更优，说明f不会比g优、
5.如果中点处相等，说明f和g这个区间里值一样，对于模板题来说，选标号更小的。

区间插入复杂度logn，其中还要递归下传懒标记logn，时间复杂度$O(log^2 n)$
https://www.luogu.com.cn/problem/P4097

#include <iostream>
constexpr int MOD1 = 39989;
constexpr int MOD2 = 1000000000;
constexpr int MAXT = 40000;
using namespace std;
using pdi = pair<double, int>;

constexpr double eps = 1e-9;

int cmp(double x, double y) {
  if (x - y > eps) return 1;
  if (y - x > eps) return -1;
  return 0;
}

struct line {
  double k, b;
} p[100005];

int s[160005];
int cnt;

double calc(int id, int d) { return p[id].b + p[id].k * d; }

void add(int x0, int y0, int x1, int y1) {
  cnt++;
  if (x0 == x1)  // 特判直线斜率不存在的情况
    p[cnt].k = 0, p[cnt].b = max(y0, y1);
  else
    p[cnt].k = 1.0 * (y1 - y0) / (x1 - x0), p[cnt].b = y0 - p[cnt].k * x0;
}

void upd(int root, int cl, int cr, int u) {  // 对线段完全覆盖到的区间进行修改
  int &v = s[root], mid = (cl + cr) >> 1;
  int bmid = cmp(calc(u, mid), calc(v, mid));
  if (bmid == 1 || (!bmid && u < v)) swap(u, v);
  int bl = cmp(calc(u, cl), calc(v, cl)), br = cmp(calc(u, cr), calc(v, cr));
  if (bl == 1 || (!bl && u < v)) upd(root << 1, cl, mid, u);
  if (br == 1 || (!br && u < v)) upd(root << 1 | 1, mid + 1, cr, u);
}

void update(int root, int cl, int cr, int l, int r,
            int u) {  // 定位插入线段完全覆盖到的区间
  if (l <= cl && cr <= r) {
    upd(root, cl, cr, u);
    return;
  }
  int mid = (cl + cr) >> 1;
  if (l <= mid) update(root << 1, cl, mid, l, r, u);
  if (mid < r) update(root << 1 | 1, mid + 1, cr, l, r, u);
}

pdi pmax(pdi x, pdi y) {  // pair max函数
  if (cmp(x.first, y.first) == -1)
    return y;
  else if (cmp(x.first, y.first) == 1)
    return x;
  else
    return x.second < y.second ? x : y;
}

pdi query(int root, int l, int r, int d) {  // 查询
  if (r < d || d < l) return {0, 0};
  int mid = (l + r) >> 1;
  double res = calc(s[root], d);
  if (l == r) return {res, s[root]};
  return pmax({res, s[root]}, pmax(query(root << 1, l, mid, d),
                                   query(root << 1 | 1, mid + 1, r, d)));
}

int main() {
  ios::sync_with_stdio(false);
  int n, lastans = 0;
  cin >> n;
  while (n--) {
    int op;
    cin >> op;
    if (op == 1) {
      int x0, y0, x1, y1;
      cin >> x0 >> y0 >> x1 >> y1;
      x0 = (x0 + lastans - 1 + MOD1) % MOD1 + 1,
      x1 = (x1 + lastans - 1 + MOD1) % MOD1 + 1;
      y0 = (y0 + lastans - 1 + MOD2) % MOD2 + 1,
      y1 = (y1 + lastans - 1 + MOD2) % MOD2 + 1;
      if (x0 > x1) swap(x0, x1), swap(y0, y1);
      add(x0, y0, x1, y1);
      update(1, 1, MOD1, x0, x1, cnt);
    } else {
      int x;
      cin >> x;
      x = (x + lastans - 1 + MOD1) % MOD1 + 1;
      cout << (lastans = query(1, 1, MOD1, x).second) << endl;
    }
  }
  return 0;
}