vp。

队友是 masterhuang，ppip。

黄大师：MO 大神，xcpc 经验丰富。

策略混乱邪恶。

I

完美回文串就是仅有一个字符的串啦……

我签签签。

G

反悔贪心一下即可（是不是把这个题讲的太高大上了）

我签签签。

A

ppip 说是二维数点板子，他签签签。

D

我们考虑二分，然后问题转化为了能否使得 $k$ 个数 $\geq x$。

我们不难处理出“如果要使得 $a_i \geq x$，$p$ 的取值区间”，然后用差分统计出对于每一个 $p$ 有几个数 $\geq x$ 即可。

我签签签。

这时候黄大师掉进 F 的深渊了。

B

我不会做 dp，不讲了。

ppip 迅速签了这个题。

J

我不会做，不讲了。

黄大师从 F 的深渊里面出来了，但是没有切掉 F。但是他看了一眼 J 就会了于是把 J 切了。

E

ppip 做的，我不会做，不讲了。

ppip 杀疯了，黄大师接着去磕 F，我在磕 M。

M

我们考虑需要放闸门的地方是类似于 V 字形的局部最小值，或者是类似于 \_/ 或者 /_\ 这种的梯形形状，前者用叉积的正负判一下即可，后者直接看水平线两边是否都比水平线高即可。

我做的，等于号和不等于号写反了，令人啼笑皆非。

H

ppip 做的，是个大 ds，给 ds 大神 ppip 磕头了。

F

一开始，黄大师就给出了 k=8 和 k=10 的构造，并且指出只要构造出 k=9 这个题就能做了。

然后我写完 M 开始用 geogebra 构造 k=9 的解。

首先我们注意到一个内部点上只有四条边是不太行的，所以我先胡了一个这样的拓扑结构。

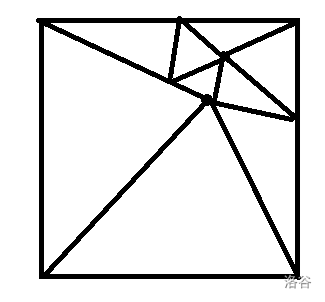
然后我就不断的调试。我使用了类似于黄大师构造的方法，假设每个点都在正方形 20*20 等分的格点上，然后，我得出了一个解（？）

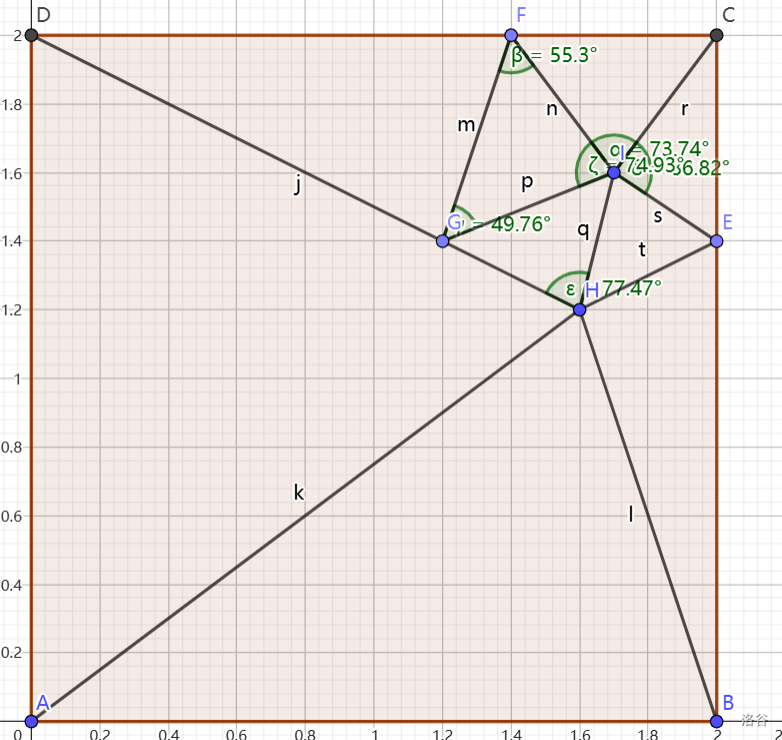
但是实际上角 EHB 是钝角，然后我对于这个解进行了一些微调，得出了真正的解。

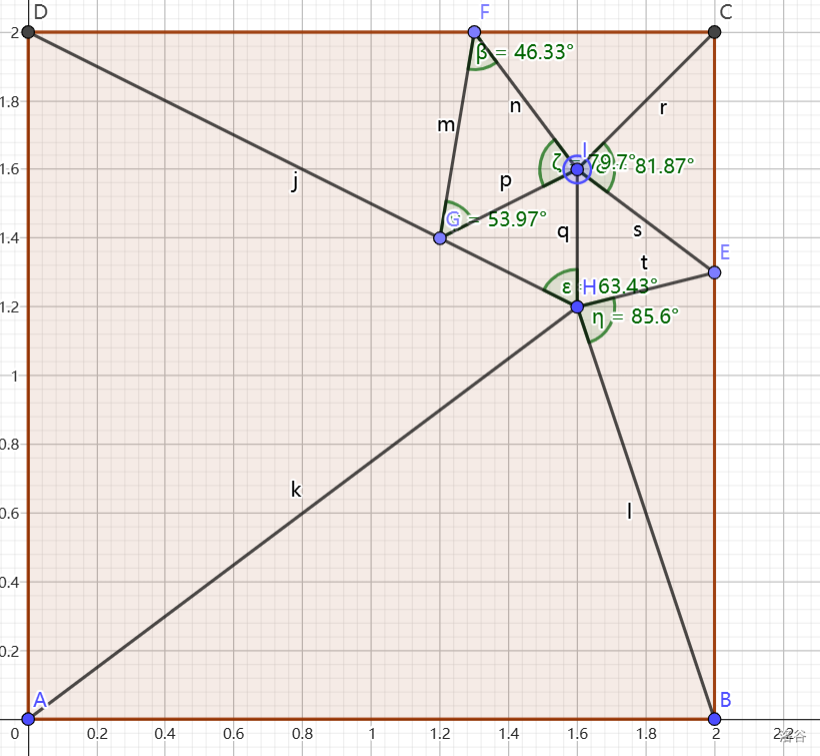
至此，这个捧杯题便被我们解决了。

有了 n 得出 n+3 的解的方法是，随机挑选一个锐角三角形把它的中点互相连接。

k=8 k=9 的构造和题解完全相同，k=10 的构造黄大师说和题解不一样，但是我并没有要到图片，很难过。

考场上只过了两个人的原因大概是考场没有 geogebra（笑哭）

C

首先 2 操作完全没用，可以用 1 操作代替。因为有 1 操作所以整个棋盘可以随意排布。

然后我们考虑时光倒流，把 3 操作替换为选定一个匹配的配方，然后把里面的字符全部变成通配符。由于我们可以随意排布棋盘，所以能匹配等价于配方中的字符是棋盘中字符的子集（通配符随意替换）

然后不断的使用这个配方直到，它只能用通配符来匹配，然后扔掉这个配方并重复这个过程。

所有配方都不能用之后，如果初始配方不能匹配就是无解。否则我们已经构造了解。

这个做法是 ppip 给我讲的，当时只剩 1h 了，然后让我冲一把。很可惜的是我的码力不是很给力，没写出来。

赛后看题解结果剩下的三个题都看不懂，我真失败。