attention is all you need

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

attention is all you need

作者：

巷港 , 2024-11-20 14:45:28 , 所有人可见 , 阅读 3

前面我们主要说的是seq2seq中的attention机制应用，但还是借助了像rnn这样的架构，不是纯正的attention。

我们比较熟知的，还得是17年Google那篇惊世之作 Attention Is All You Need

因此，我们这次彻底学一下纯attention的应用和著名且十分重要的transformer架构！

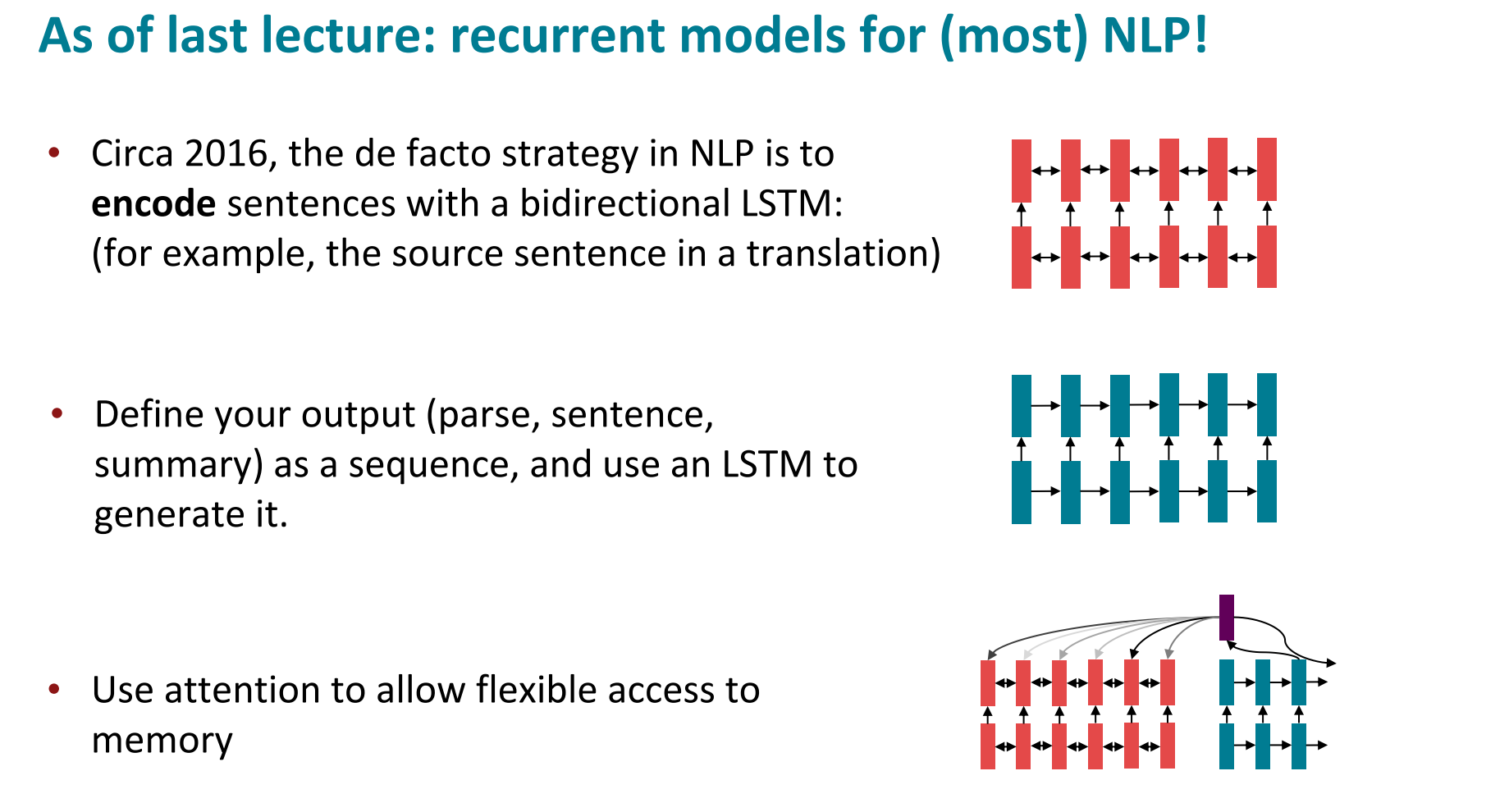
在transformer出道之前，nlp流行的还是rnns系列的模型架构，在这种seq2seq中加入attention解决encoder信息记忆问题，如下：

根据这些问题，transformer提出就有了动机：

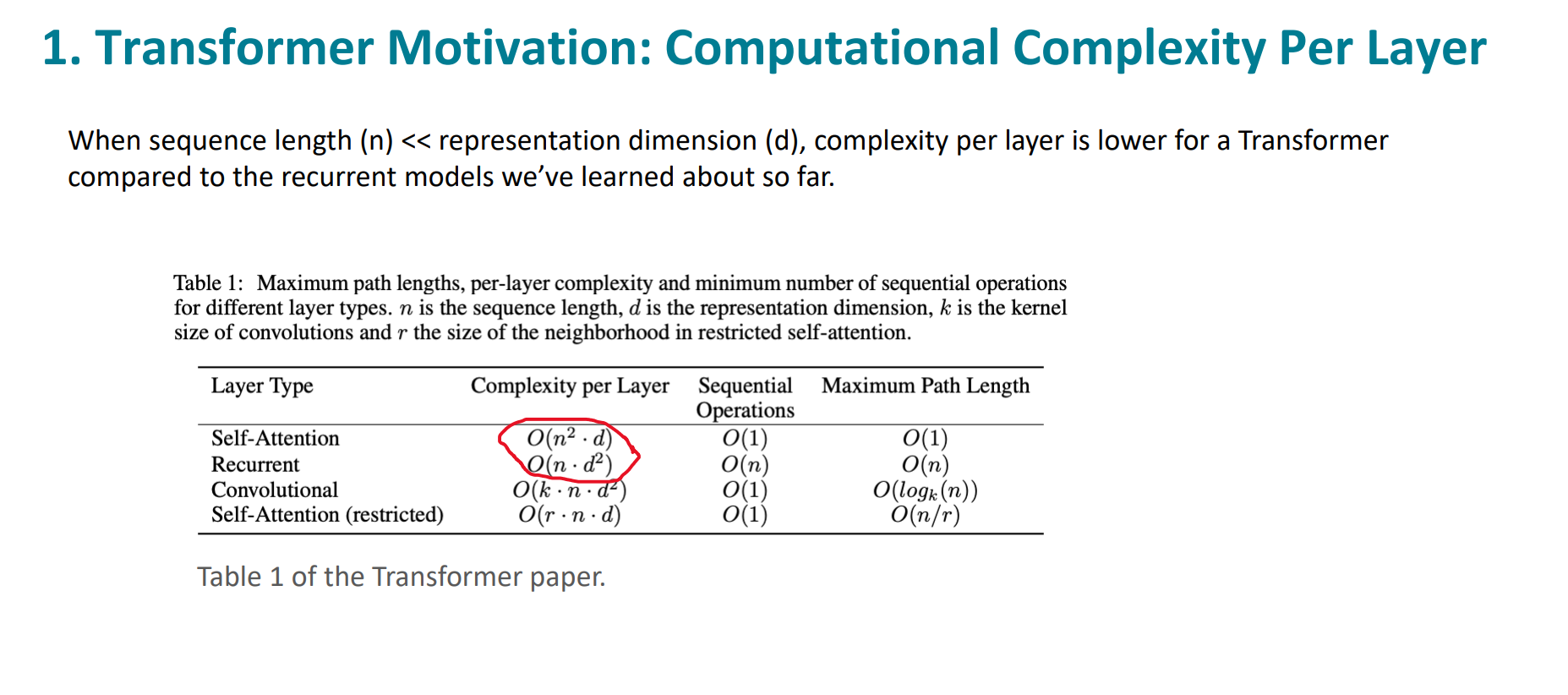
第一条，模型复杂度的问题。

可以看到，RNN的时间复杂度为$O(n\cdotd^2)$，self-attention的复杂度为$O(n^2\cdot d)$

其中n是序列长度，d是向量的表示维度。

在n远小于d的时候，self-attention的复杂度是更好的。

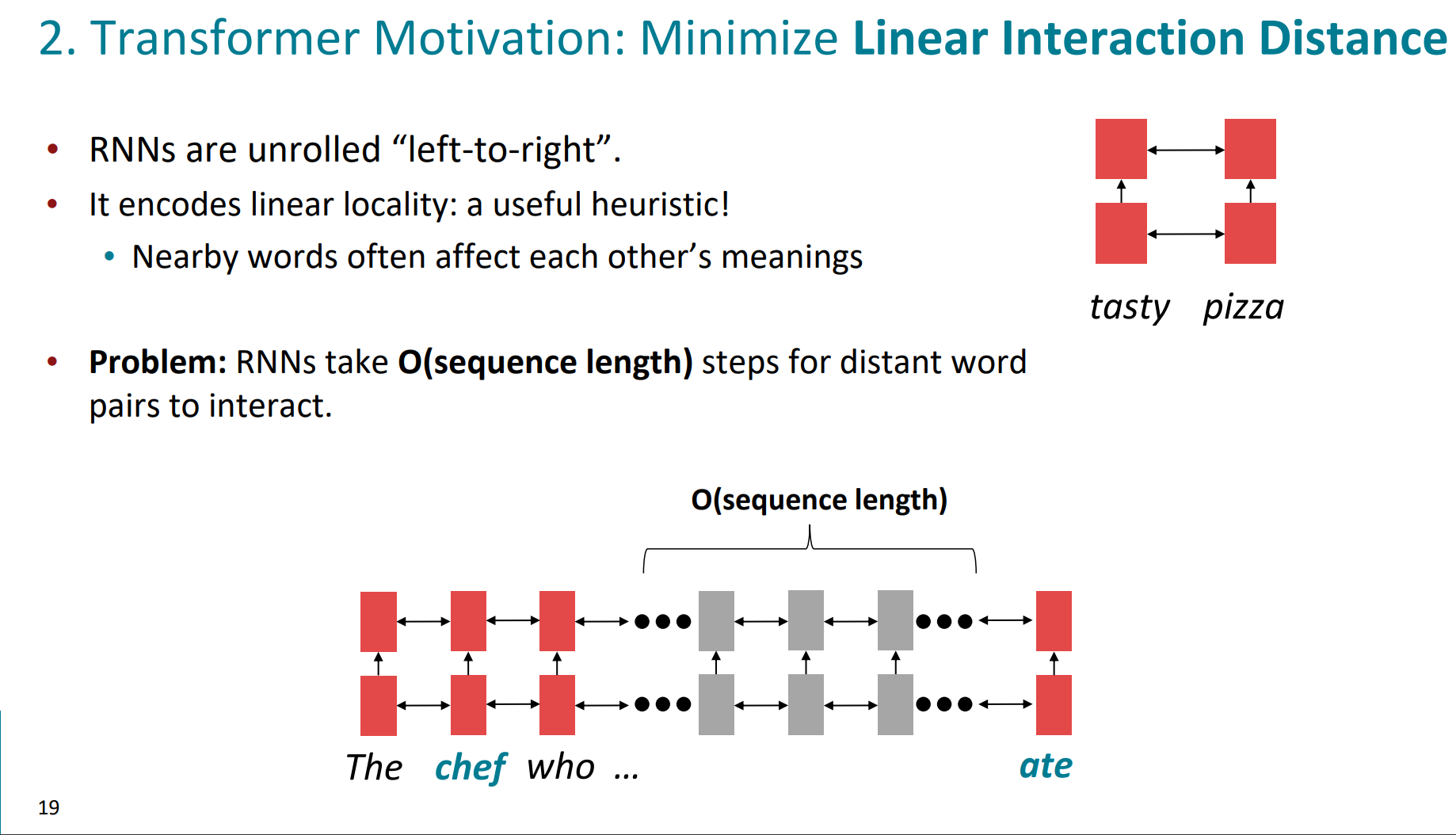
第二条，词与词的线性相互作用距离。

我们知道rnn是left-right的典型代表，当前位置词的语义是受到周边词的影响的。但是距离一旦变长，由于梯度消失等问题，模型就很难去捕捉词与词之间的关系了。

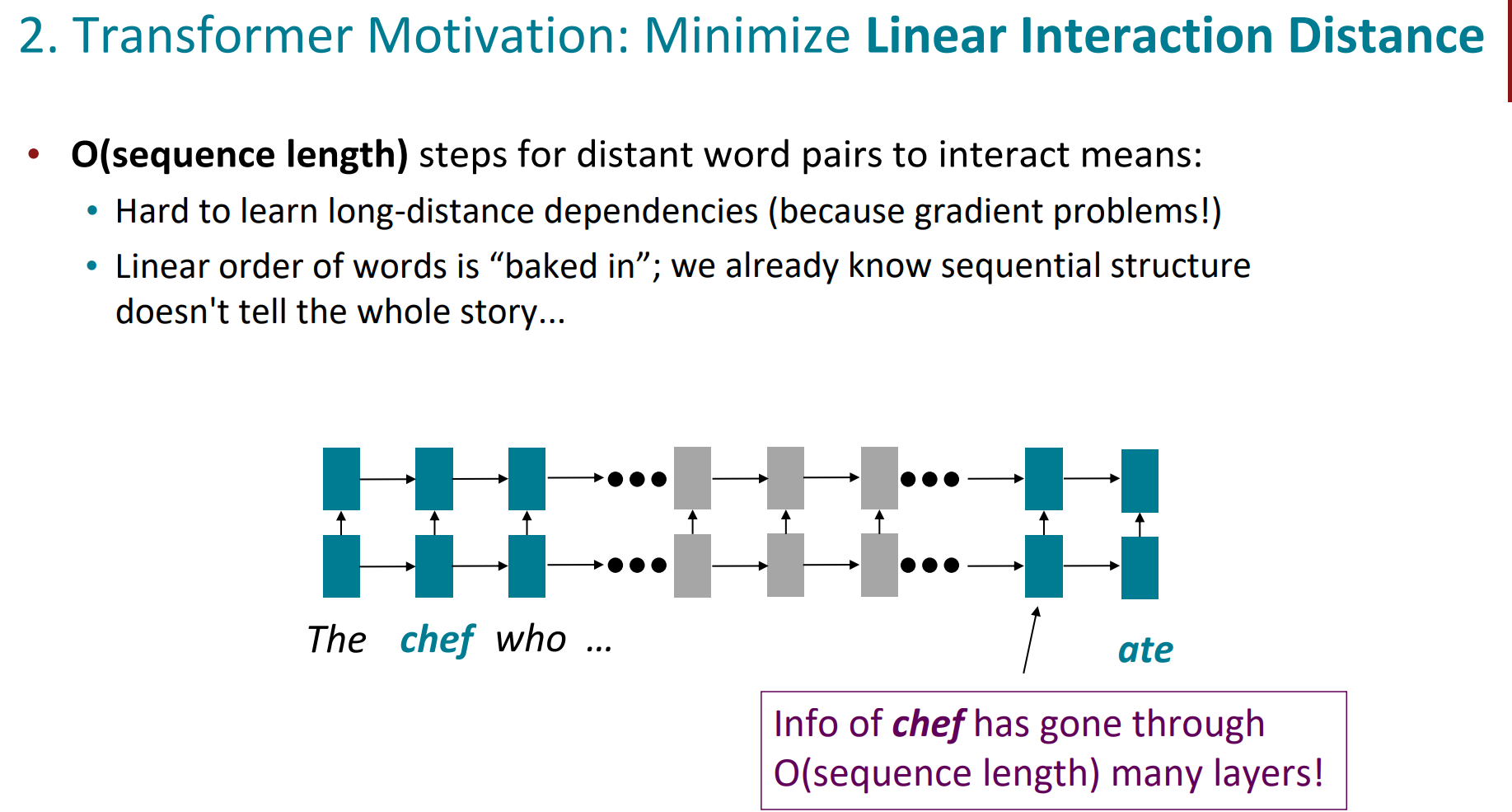
第三条，就是并行化的问题。

我们知道rnn这样一种典型的序列模型，在前一个hidden state被计算出来之前，之后的位置是无法被计算出来的，所以这就很难去并行化操作，大大限制了GPU的能力。计算资源利用不起来，计算速度提不上去。

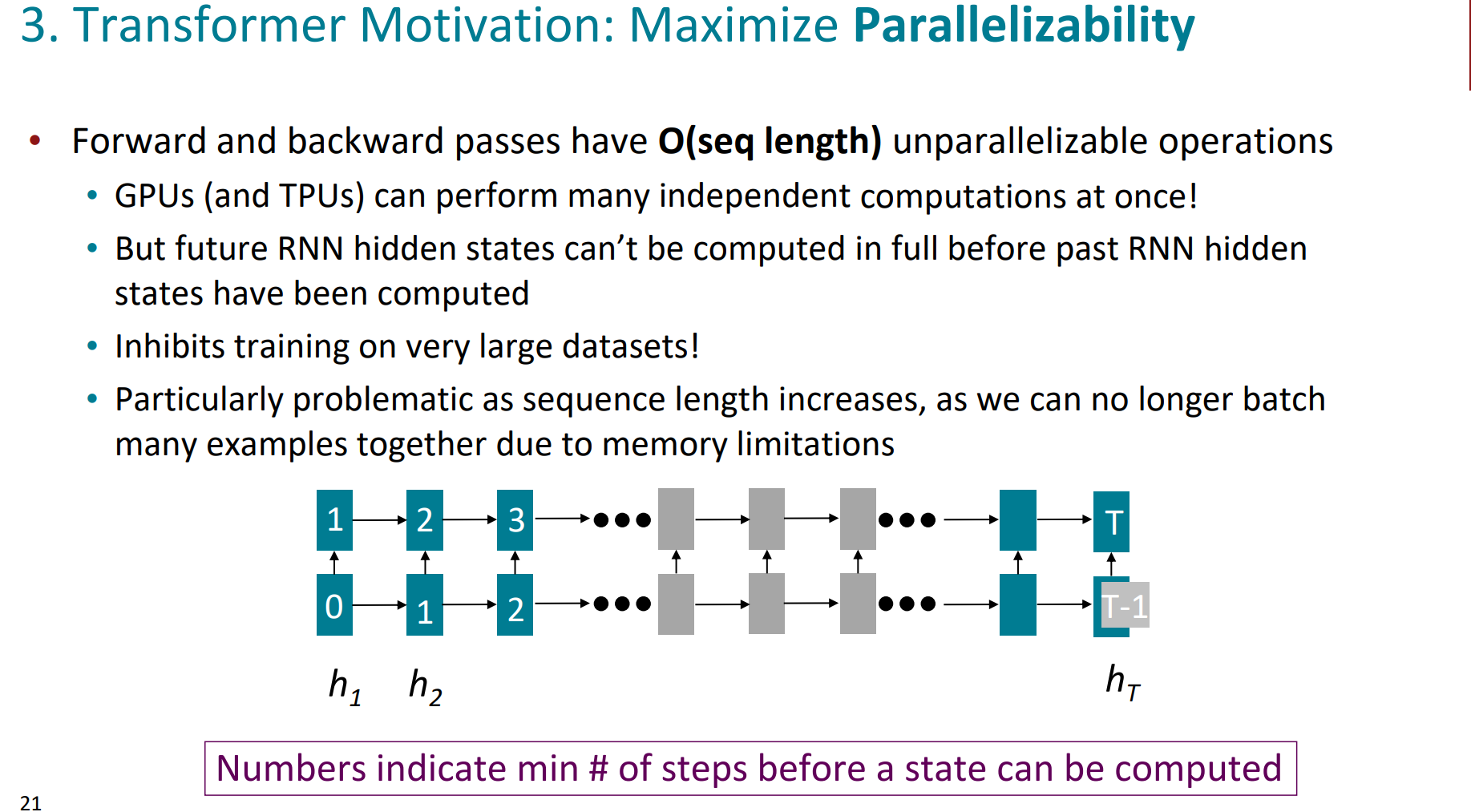
就到了正式看transformer中的attention了。

我们前面看到的attention是decoder-encoder的，即decoder的每个hidden state是一个query，对应的encoder所有的hidden state是values。但这里的attention是self-attention，即encoder-encoder或者decoder-decoder。也就是query和values是一致的。

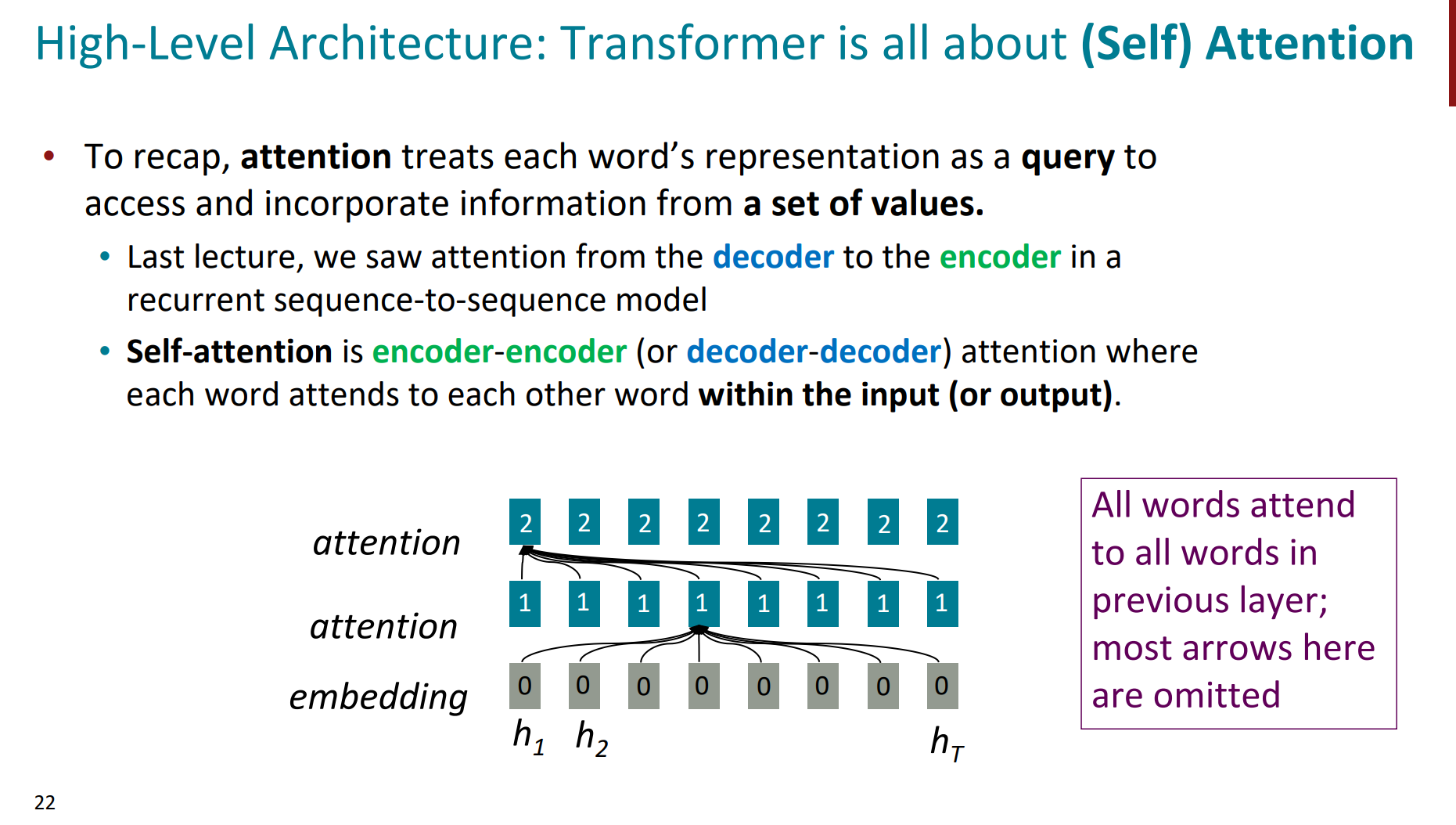
下面这张图也就很清晰能看出rnn的attention和transformer的attention的区别：

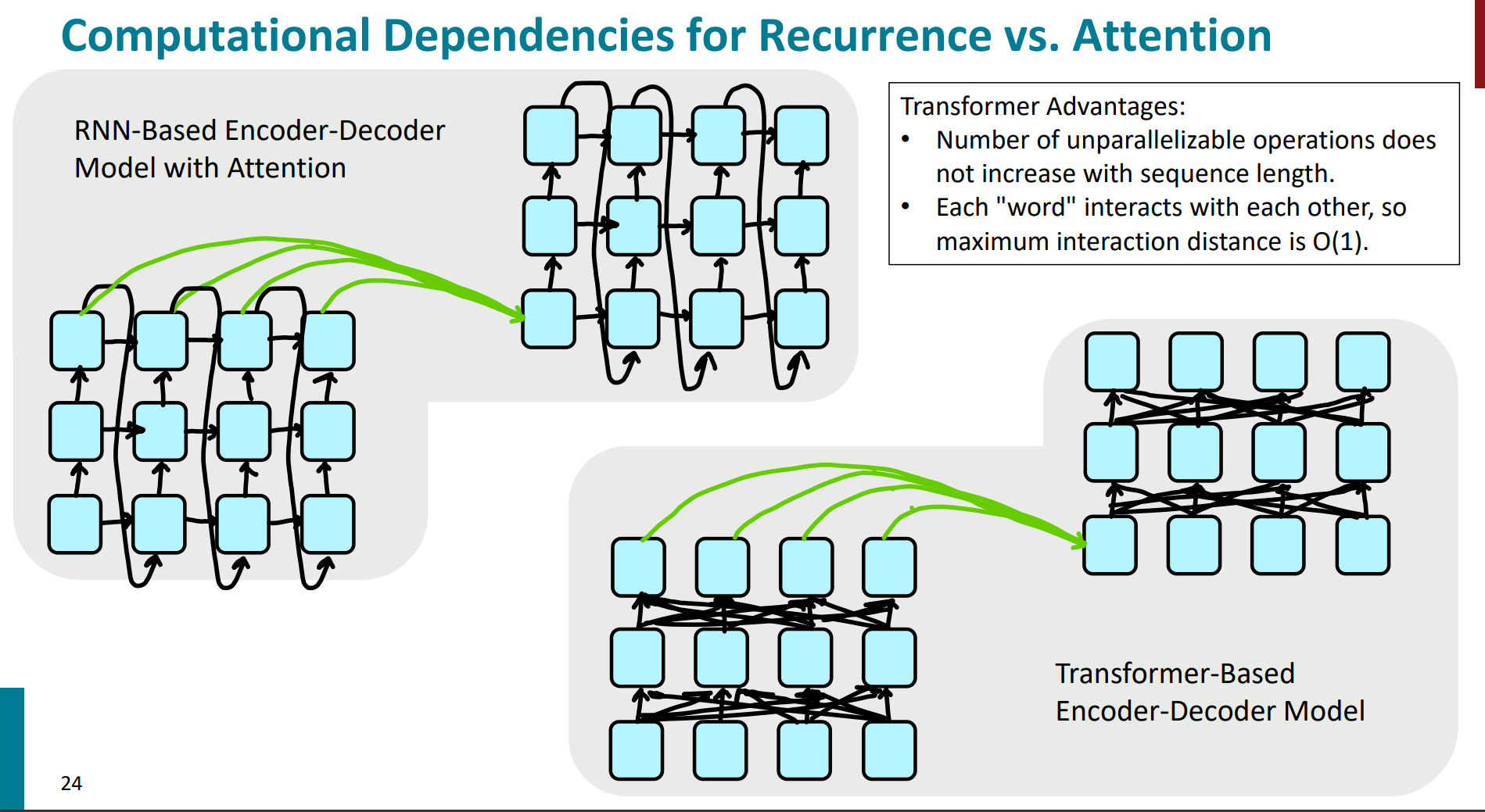
rnn中每个方块（代表时间步）都通过箭头与前后的方块相连，典型的串行依赖。
transformer中让每个位置的“单词”都可以直接访问序列中的其他位置，每个节点可以直接连接到其他节点，减小了交互的最大距离，使得每个“单词”在一次计算中即可和其他“单词”交互，极大地提高了并行计算的效率，复杂度直接变为了$O(1)$

到这里，我们基本了解知道了transformer产生的动机以及其与rnn相比的优点。

接下来，我们就得正式去读懂transformer的架构了。这是当前最火最流行，也会在未来相当长一段时间里主流的模型架构，必须得读透读懂。

我们按照先encoder再decoder的顺序去深挖。

而self-attention作为这两大模块中的核心部分，我们需要先单独拎出来搞懂。

self-attention

我们先看一下常见的数据结构哈希表hashtable：

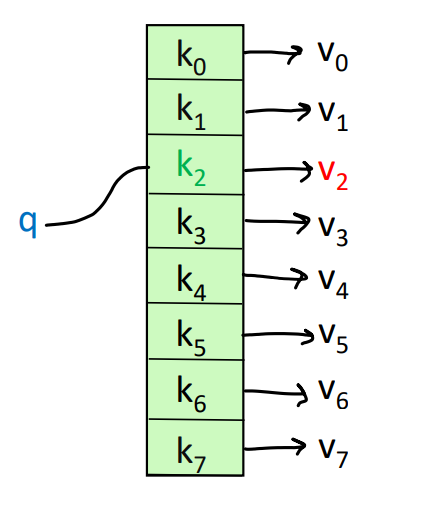
可以看出，对于每一个待查询的query，去哈希表里找键值对key-value，都会有一个一一对应的唯一存在的。比如下图的，我用query去查k2对应的value，那就唯一对应一个v2的值。

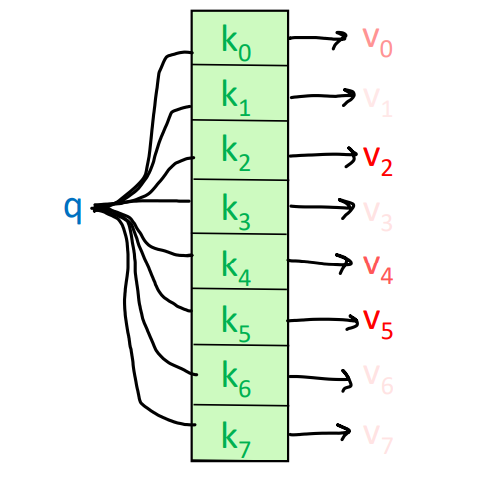
而自注意力机制，则是对于待查询的query，匹配每个key的时候，每一个key都会有一个不同程度的对应，而不是唯一的值对应。如下图，我去查query对应每个key的value，我们发现每个key都会有一个value值，只是程度（值的大小）不同，这就代表着query对这个key的重要程度不同。比如图中，我的这个query，可能和k2，k4和k5更匹配一些，因此对应的value值就更大。

那么形象的概述性的计算过程就呼之欲出了：

根据同样的输入$x_i$分别计算$q_i$，$k_i$和$v_i$，也就是得到我们常说的q，k，v
计算q和k的得分score，即二者点乘。
对q和k的不同得分进行softmax归一化处理，得到了不同的socre对应的权重$\alpha_i$，也就是对应的一种概率分布。
将权重和value进行加权求和，得到一种新的表示。

整个的过程可以概括为下面的公式：

$$Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V$$

这里我们注意，虽然表示可以很简单，但我们不能忘，输入x，q，k，v都是矩阵，因此还是下图的表示更真实：

我们可以进一步形象化注意力机制的计算过程，以机器翻译这个任务为例。

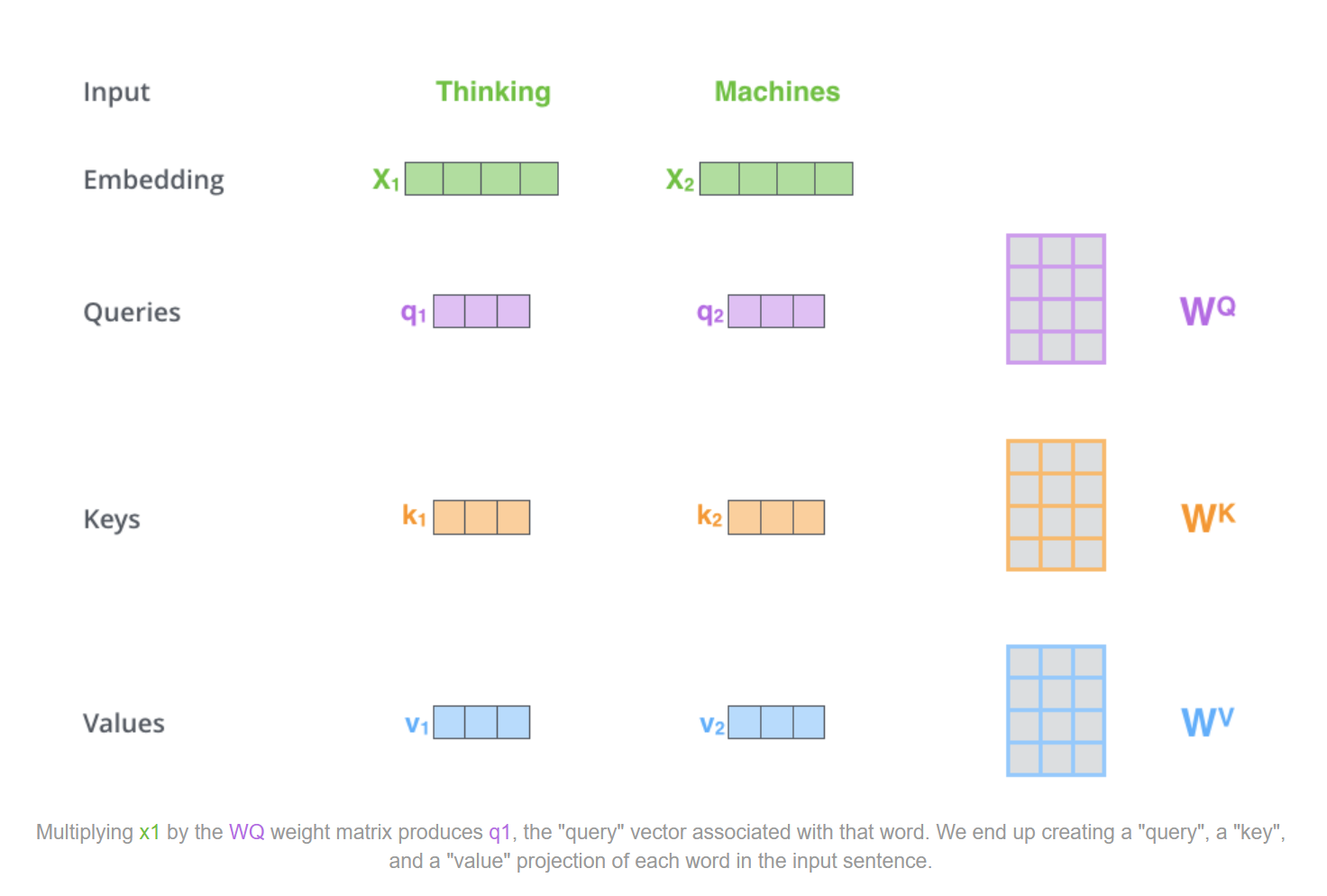
我们假设要翻译thinking machines。现在获取了二者的embedding vectors。

我们以单一的向量计算为例。

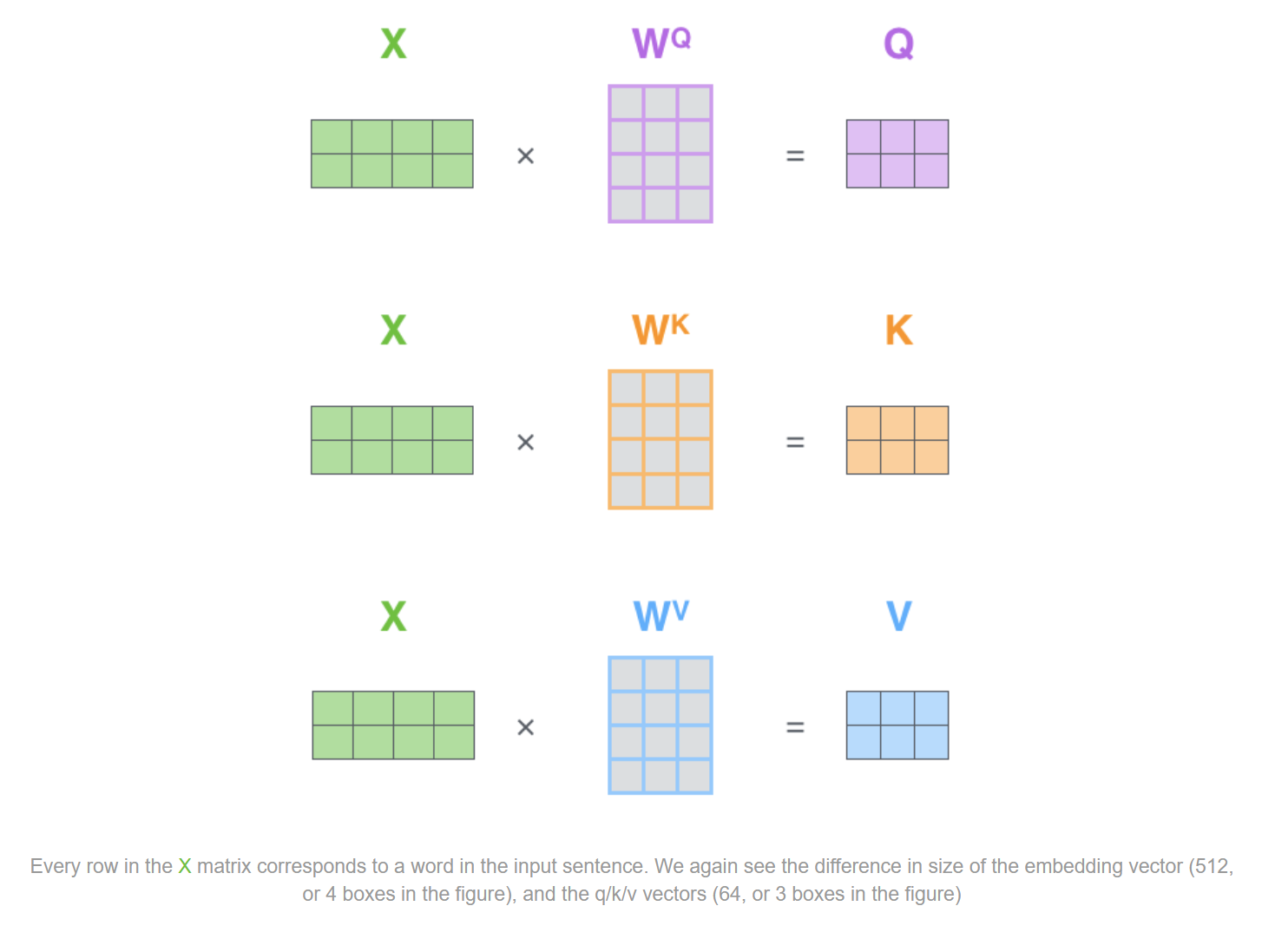
首先，是要创造出q，k，v三个向量。创造的方法也很简单，就是用输入的词嵌入向量和三个不同的矩阵相乘，这三个矩阵分别为$W^Q$，$W_K$，$W_V$，是我们后面在模型训练过程要训练出来的三个参数矩阵。这里注意：我们得到的这三个vectors的维度一般远小于embedding的维度（embedding是512，qkv一般是64）。

但这种架构设置也不是必须的，理由是：

They don’t HAVE to be smaller, this is an architecture choice to make the computation of multiheaded attention (mostly) constant.

第二步，计算注意力的得分。假设我们计算对于第一个词thinking的注意力得分情况。那我们就需要将input的sentence中所有其他的word都来计算和当前位置的thinking的注意力分布情况。这里我们假设其他的word就是machines这一个。这里有篇博客形容的很好，这个注意力分数的含义：

We need to score each word of the input sentence against this word. The score determines how much focus to place on other parts of the input sentence as we encode a word at a certain position.

那么此时thinking就是作为query，其他词如machines就是key。我们需要做的是将当前词作为搜索的query，去和句子中所有词（包含该词本身）的key去匹配，看看相关度有多高。这里的计算就是向量之间的点积dot product。

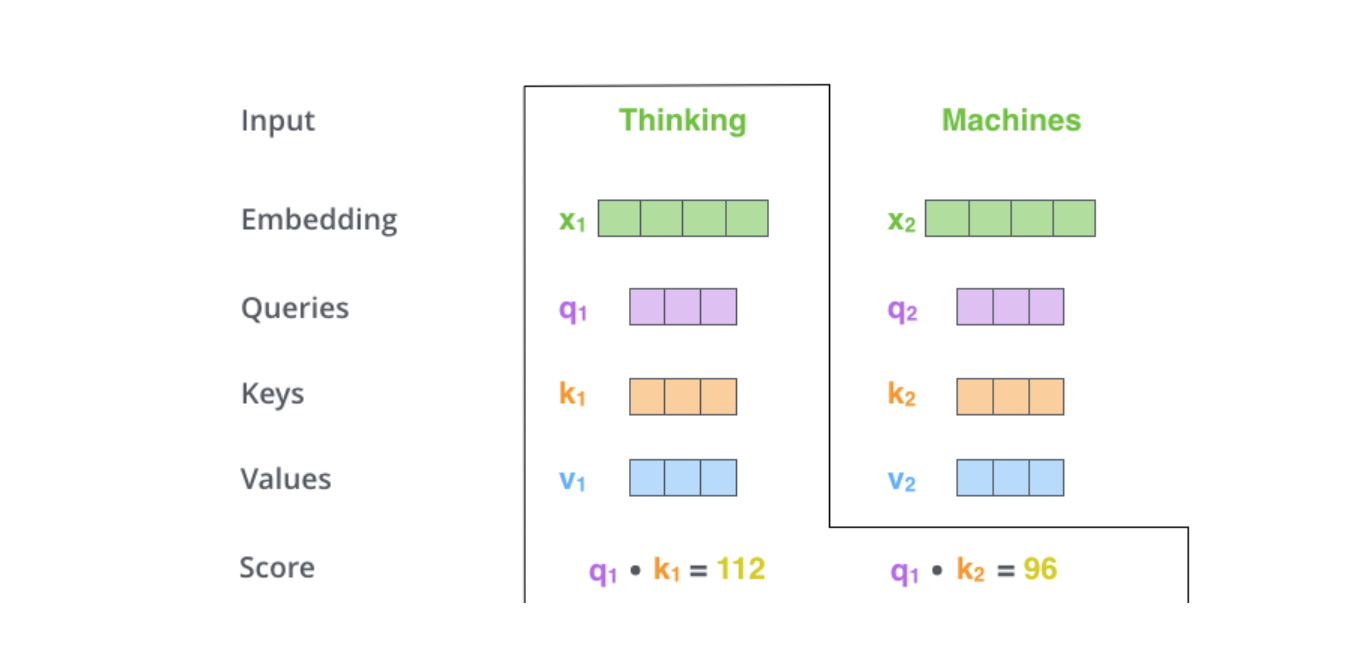
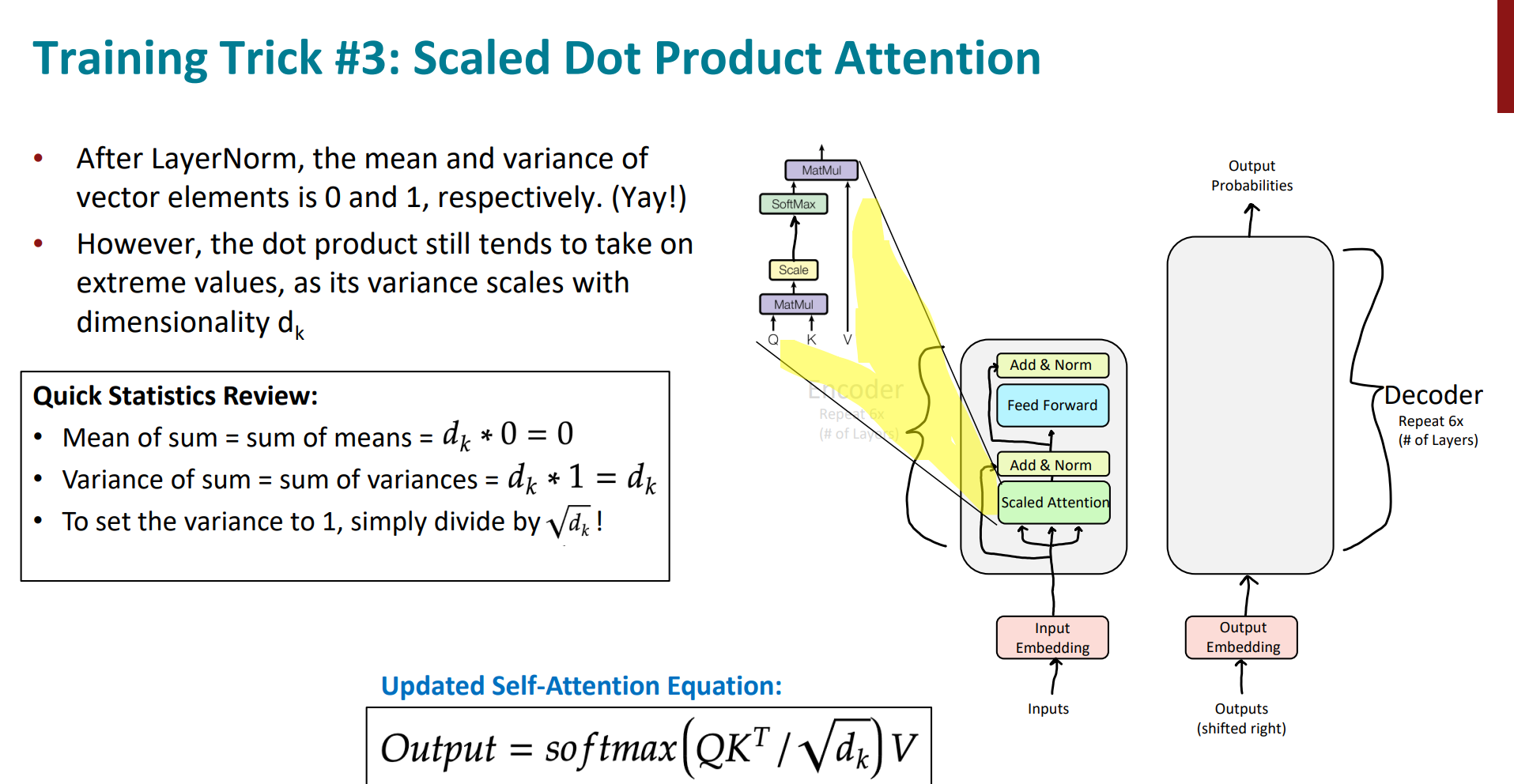
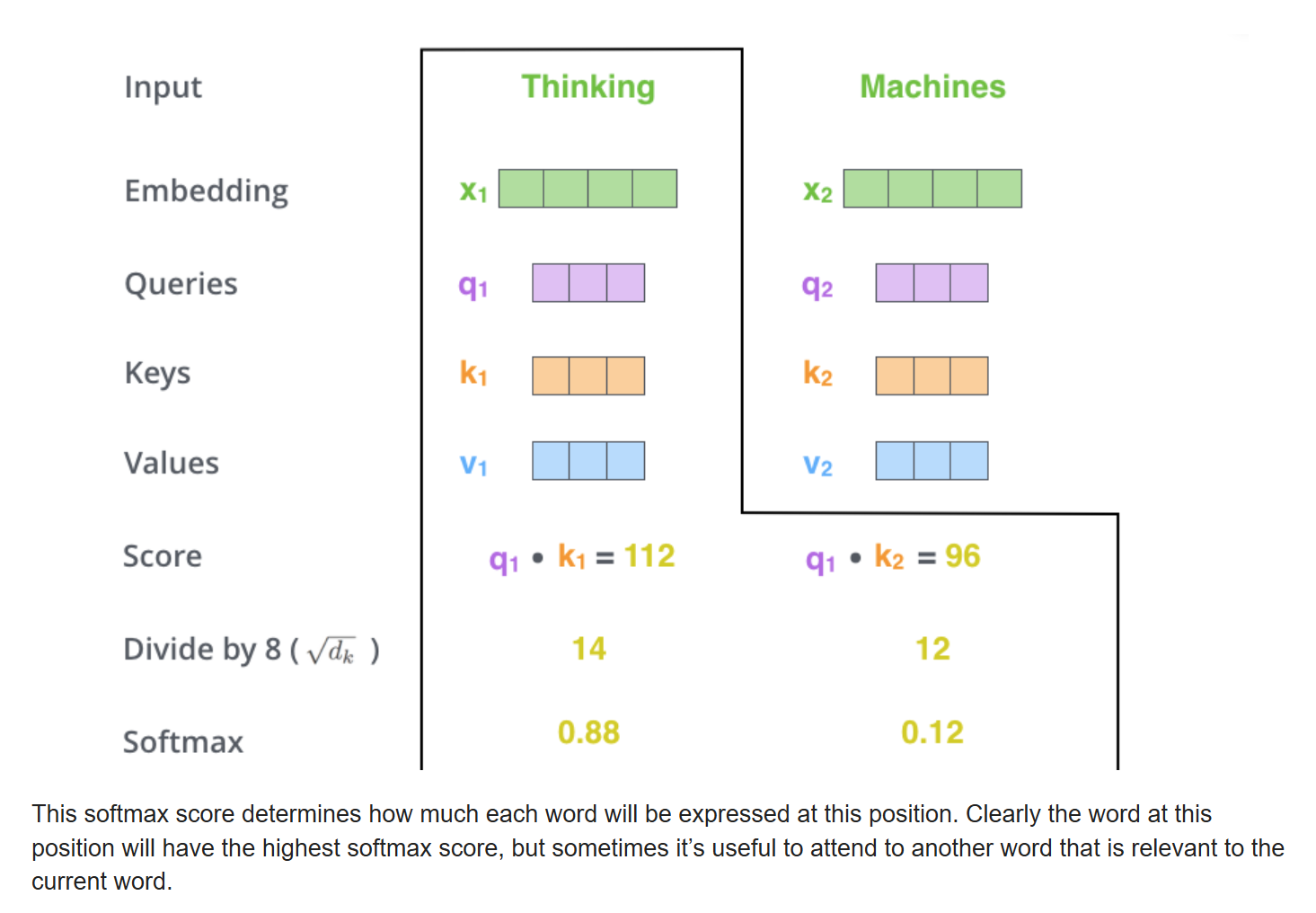
接着，做一下尺度缩放操作。这里原文章给出的是除以64的平方根即8，作用是让梯度更稳定。

当然，具体缩放的分母不是固定的，可以根据情况自己定义。然后将缩放后的结果传递给softmax函数进行归一化操作，得到概率分布。我们可以看到，一般情况下，自己和自己的注意力得分会最高，当然其他位置和自己的相关性很高的话，那得分自然也会高。

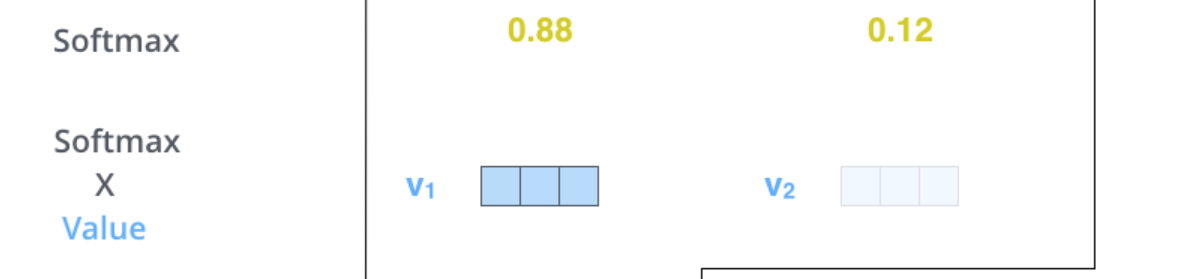
下一步，是将softmax得到的结果与各自的向量进行相乘。这里的目的就是，将得分高的向量继续保持高得分的状态，同时可以将得分很低的向量淹没掉。这样，也是为了接下来加权求和得到最终的vector做好了准备。

The fifth step is to multiply each value vector by the softmax score (in preparation to sum them up). The intuition here is to keep intact the values of the word(s) we want to focus on, and drown-out irrelevant words (by multiplying them by tiny numbers like 0.001, for example).

最后一步，就是将向量进行加权求和，得到thinking这个位置的self-attention后最终的向量。

The sixth step is to sum up the weighted value vectors. This produces the output of the self-attention layer at this position (for the first word).

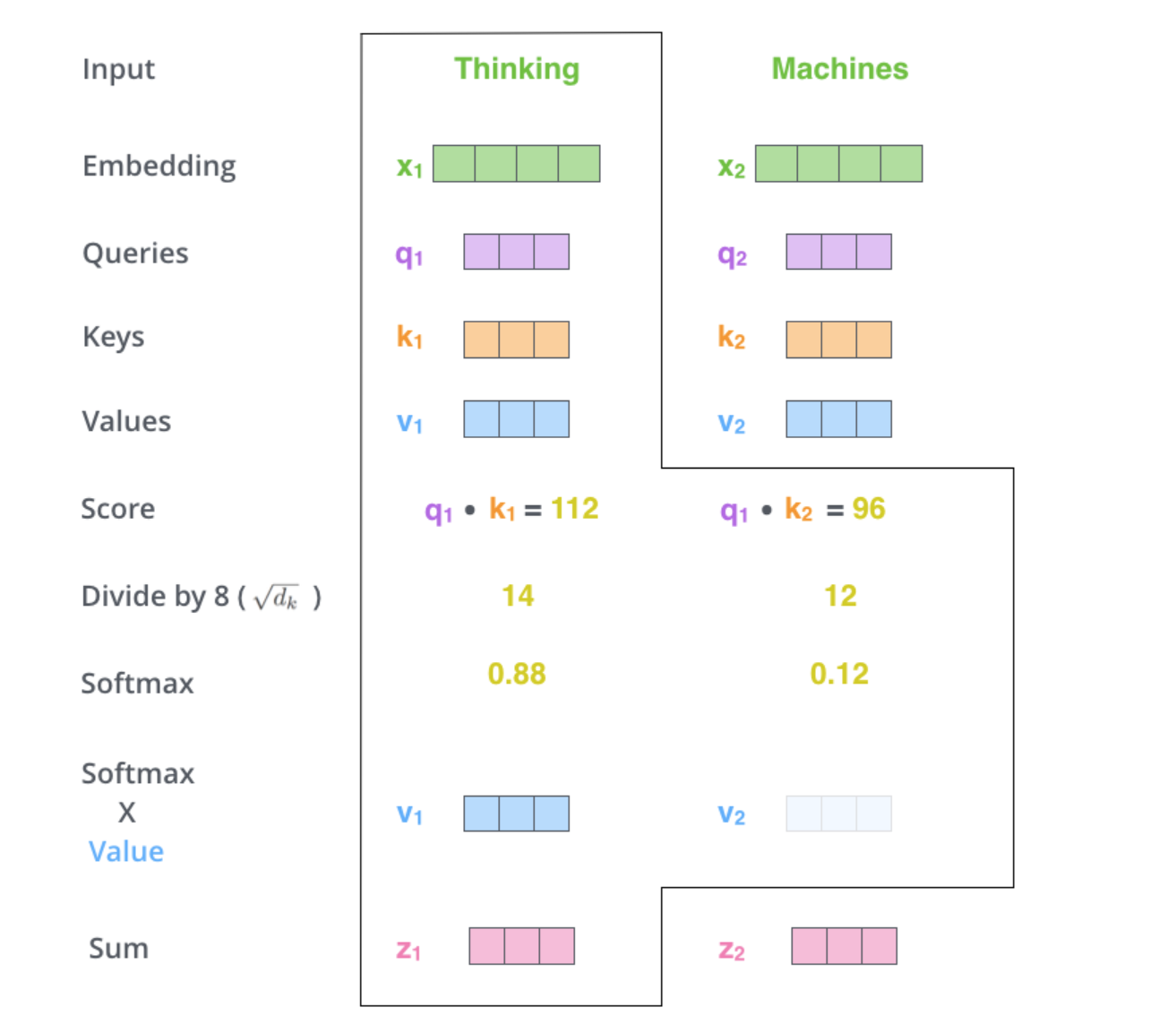
以上的过程，就完成了一个位置的self-attention的过程。

但注意，上面是以vector为单位进行计算的，实际应用中，这样太慢了，是以矩阵为单位进行计算的。

我们再看一下真实情况下，矩阵计算的自注意力机制。

我们将输入的vector进行合并，形成matrix。这里注意，每一行对应一个word的输入embedding vector。分别与$W_Q$，$W_K$，$W_V$三个矩阵进行相乘，得到Q,K,V三个矩阵。

因为我们是矩阵计算，那这样的话，接下来的步骤可以合并。即直接将Q矩阵与K矩阵进行相乘，尺度缩放之后过一个softmax得到了最终的矩阵。

到这里，我们基本对（单头）的自注意力机制有了很清晰的理解。因此，我决定直接结合矩阵计算的形式化表示符号，直观展示一下整个的计算过程：

我们首先要明确一些基本的符号数值定义的含义，尤其是每一个参数的维度，一定要清晰。

$T$：input序列的长度（即序列中有$T$个词）
$d_k$：每个词的表示向量维度（即 Query、Key的向量维度，通常是模型隐藏层的维度）。
$d_v$：value的向量维度。（一般情况下$d_k=d_v$）
输入矩阵$X$：大小为$T \times d_model$
参数矩阵$W_Q$：Query的权重矩阵，大小为$d_model \times d_k$
参数矩阵$W_K$：Key的权重矩阵，大小为$d_model \times d_k$
参数矩阵$W_V$：Value的权重矩阵，大小为$d_model \times d_v$
$Q$：Query矩阵，每一行是一个word的query向量，大小为$T \times d_k$
$K$：Key矩阵，每一行是一个word的key向量，大小为$T \times d_k$
$V$：Value矩阵，每一行是一个word的value向量，大小为$T \times d_v$

核心计算的过程（公式）：

$$\text{Attention}(Q,K,V)=\text{Softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V$$

$QK^{\top}$：点积计算，生成注意力分数矩阵，大小为$T \times T$
Softmax：对每一行归一化，将分数矩阵转换为注意力权重矩阵，大小仍为$T \times T$
注意力权重矩阵与V相乘，生成attention最后的输出矩阵：大小为$T \times d_v$

将这个过程形式化表示如下，可能更清晰直观一些：

$$QK^\top=\begin{bmatrix}q_1^\top\\q_2^\top\\\vdots\\q_T^\top\end{bmatrix}\cdot\begin{bmatrix}k_1&k_2&\cdots&k_T\end{bmatrix}=\begin{bmatrix}q_1^\top k_1&q_1^\top k_2&\cdots&q_1^\top k_T\\q_2^\top k_1&q_2^\top k_2&\cdots&q_2^\top k_T\\\vdots&\vdots&\ddots&\vdots\\q_T^\top k_1&q_T^\top k_2&\cdots&q_T^\top k_T\end{bmatrix}$$

生成大小为$T \times T$的矩阵，每个元素(i,j)表示第i个query与第j个key的向量点积值。

$$QK_{\mathrm{scaled}}^\top=\frac{QK^\top}{\sqrt{d_k}}$$

矩阵中的每个元素除以$\sqrt{d_k}$实现缩放。

\text{Softmax}(QK^\top_{\text{scaled}}){ij} = \frac{\exp(QK^\top{\text{scaled}}{ij})}{\sum{j=1}^T \exp(QK^\top_{\text{scaled}}_{ij})}

对矩阵的每一行softmax，实现将得分矩阵转化为注意力权重矩阵。

$$\begin{aligned}\text{Attention Weights}&=\begin{bmatrix}\alpha_{11}&\alpha_{12}&\cdots&\alpha_{1T}\\\alpha_{21}&\alpha_{22}&\cdots&\alpha_{2T}\\\vdots&\vdots&\ddots&\vdots\\\alpha_{T1}&\alpha_{T2}&\cdots&\alpha_{TT}\end{bmatrix}\end{aligned}$$

此时softmax矩阵的大小还是$T \times T$，每一行的$\alpha_{i,j}$是i对j的注意力权重因子。

这时候V矩阵登场，如下：

$$V=\begin{bmatrix}v_1^\top\\v_2^\top\\\vdots\\v_T^\top\end{bmatrix}=\begin{bmatrix}v_{11}&v_{12}&\cdots&v_{1d_v}\\v_{21}&v_{22}&\cdots&v_{2d_v}\\\vdots&\vdots&\ddots&\vdots\\v_{T1}&v_{T2}&\cdots&v_{Td_v}\end{bmatrix}$$

$$\text{Output}=\begin{bmatrix}\sum_{k=1}^T\alpha_{1k}v_k\\\sum_{k=1}^T\alpha_{2k}v_k\\\vdots\\\sum_{k=1}^T\alpha_{Tk}v_k\end{bmatrix}$$

这时候得到了最终的矩阵输出，每一行是经过注意力权重加权求和后的 Value 表示，包含上下文信息。矩阵大小为$T \times d_v$

这里注意，self-attention不是万能的，也有局限性。那就是整个过程没有非线性元素的参与，所以本质还是线性变换，这是不够的。

解决办法也很简单，就是在self-attention之后加一个前馈神经网络feedforward network。这样存在的激活函数就可以有了非线性的存在。

我们在self-attention中是attend那些与i位置得分高的word，那如果我们想同时看一下这个sentence中还有哪些位置值得从不同角度去关注？

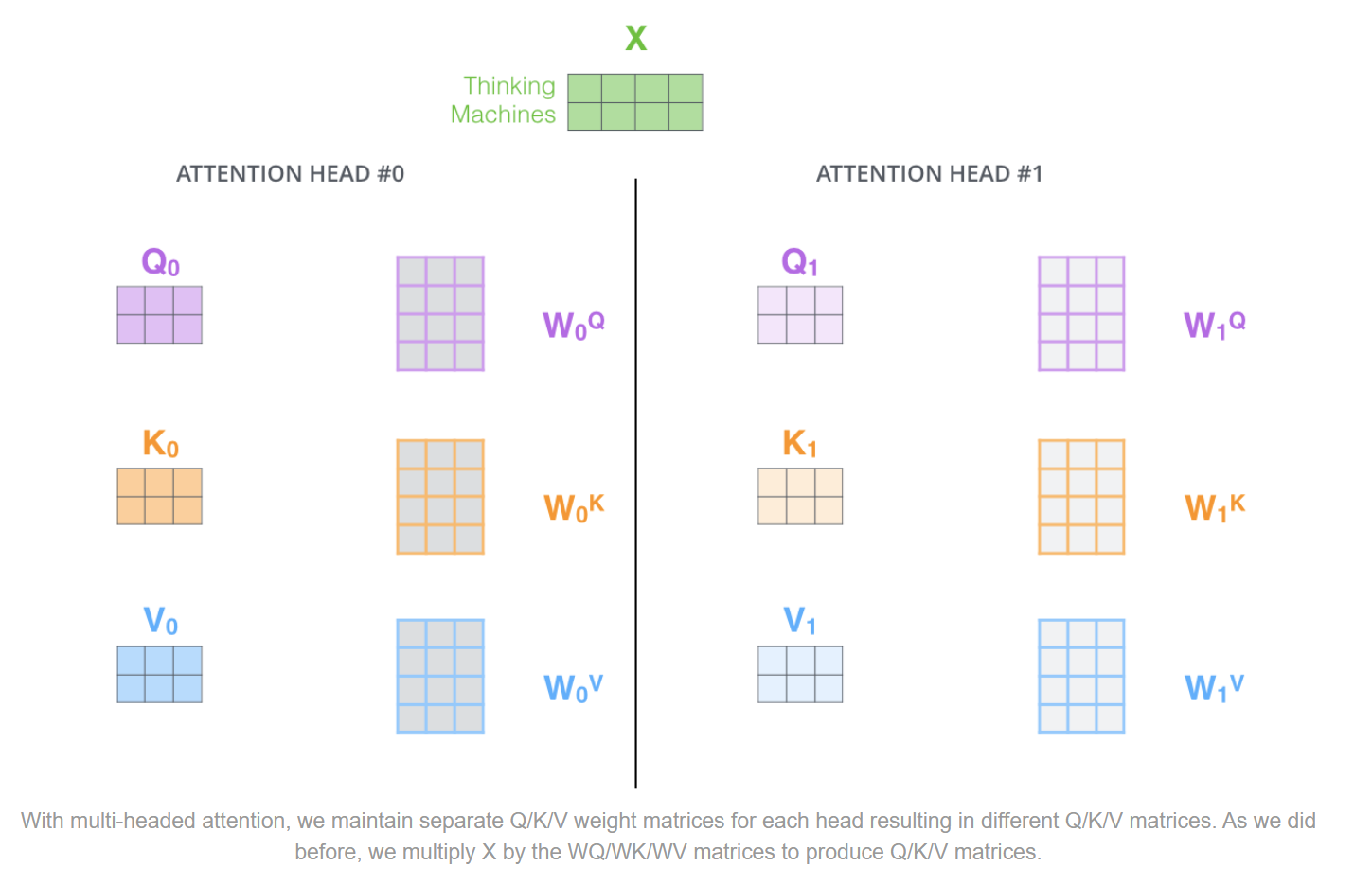
那么多头自注意力机制，其实不同点，就是可以有多种QKV的矩阵表示。我们详细看一下。

以两个head为例，其实就是可以初始化两类独立的W矩阵（两套W），这样我们可以将$X$分别与$W_0^{Q},W_0^{K},W_0^{V}$和$W_1^{Q},W_1^{K},W_1^{V}$相乘，得到两套QKV。

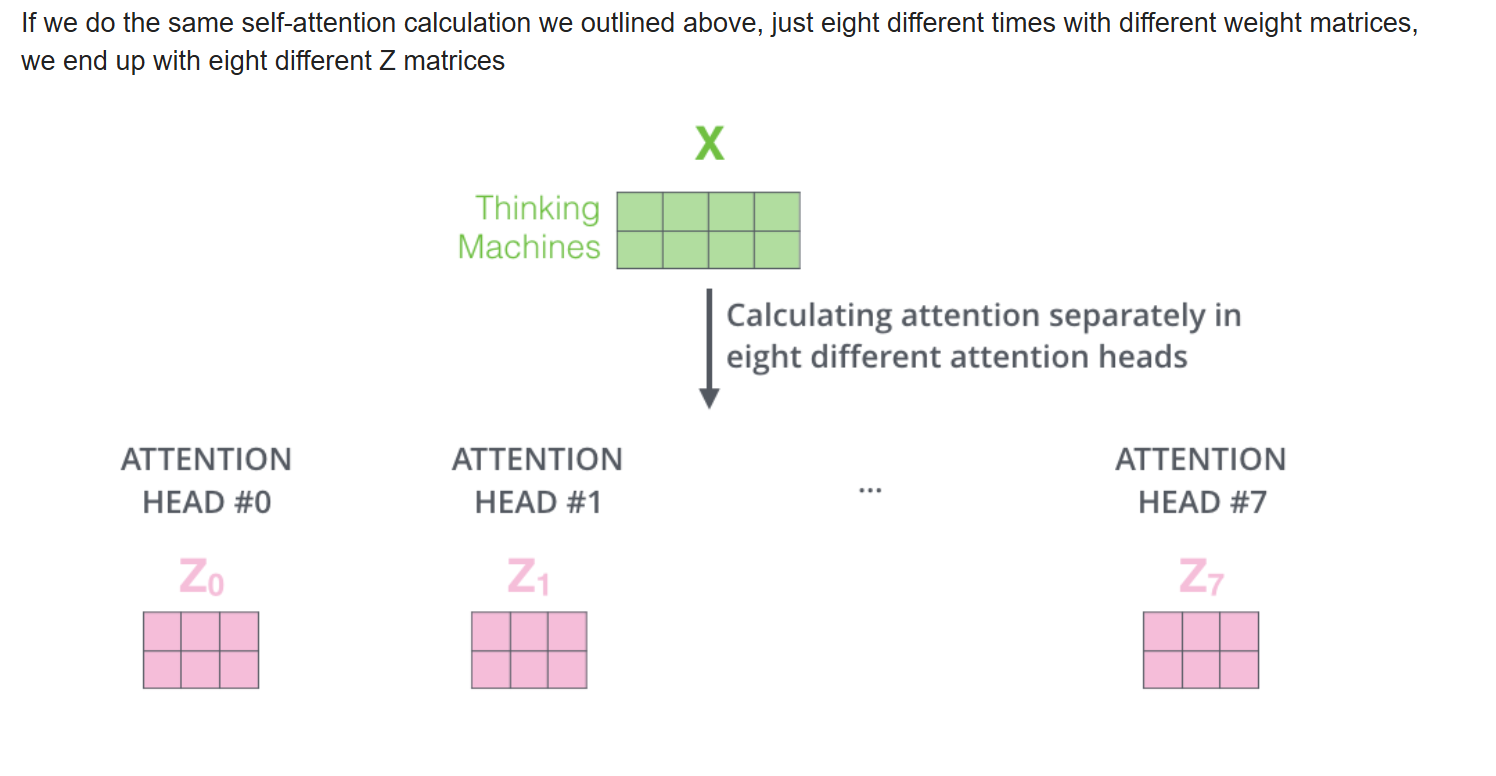
文章用的是8个head。但如果还是像上面那样计算，那么我们会得到8个独立的Z矩阵。但这样不利于传入到网络中，网络更希望看到的是一个单独的矩阵，即每个word对应一个独立的vector。因此，我们需要做的是将这8个矩阵压缩合并为一个矩阵。

方法是将这几个Z矩阵拼接起来，与一个新的权重矩阵$W_O$相乘，得到最终的多头注意力矩阵Z。

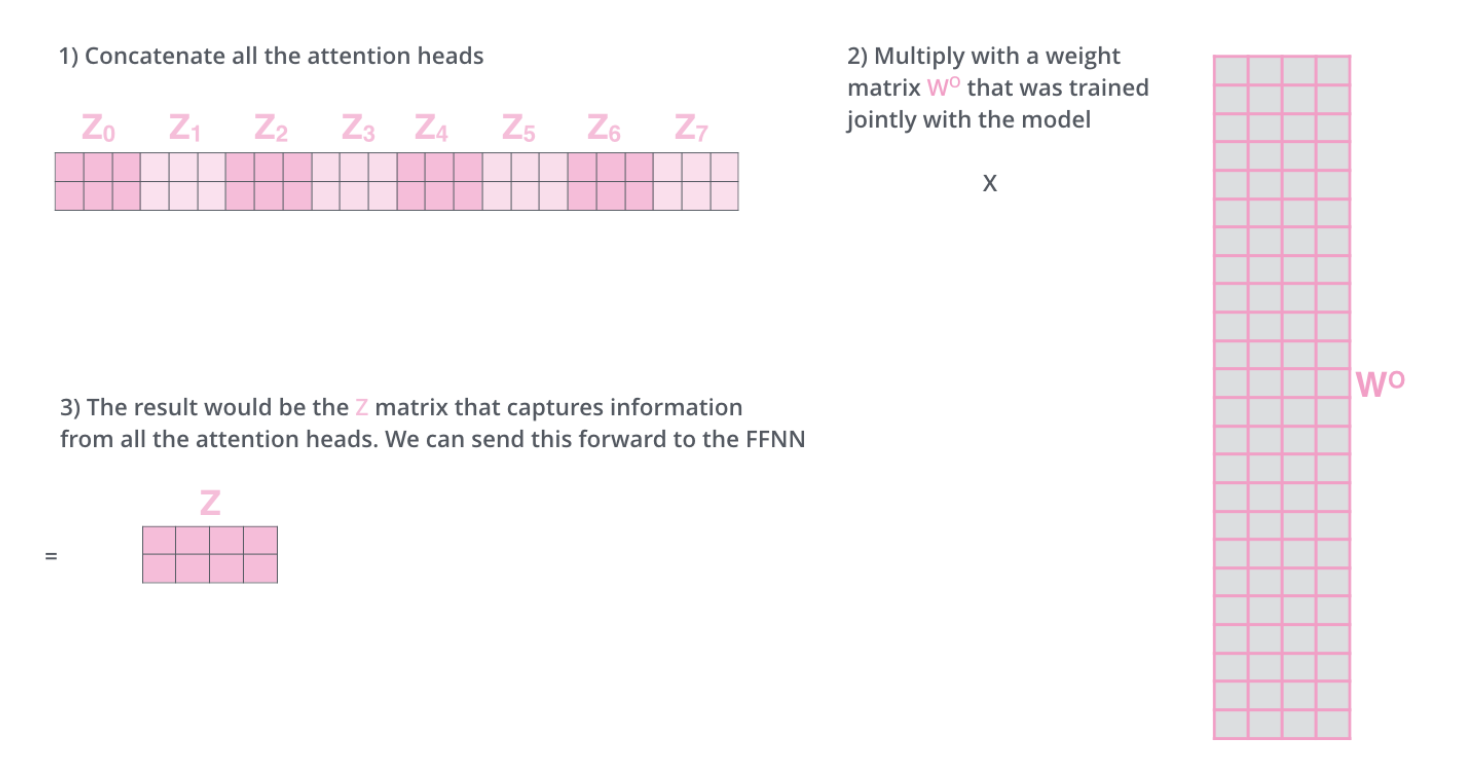
到这里我们基本完成了多头注意力机制的理解。

以一个例子加深一下理解，比如说一句话：The animal didn’t cross the street because it was too tired。

我们用self-attention对it计算，那么大概率是animal得分更高。

如果用多头，那么不仅能得到animal的得分更好，可能还有其他词也会有高得分，比如tired等。这就意味着我们能获得不同位置的信息融合后的向量表示。

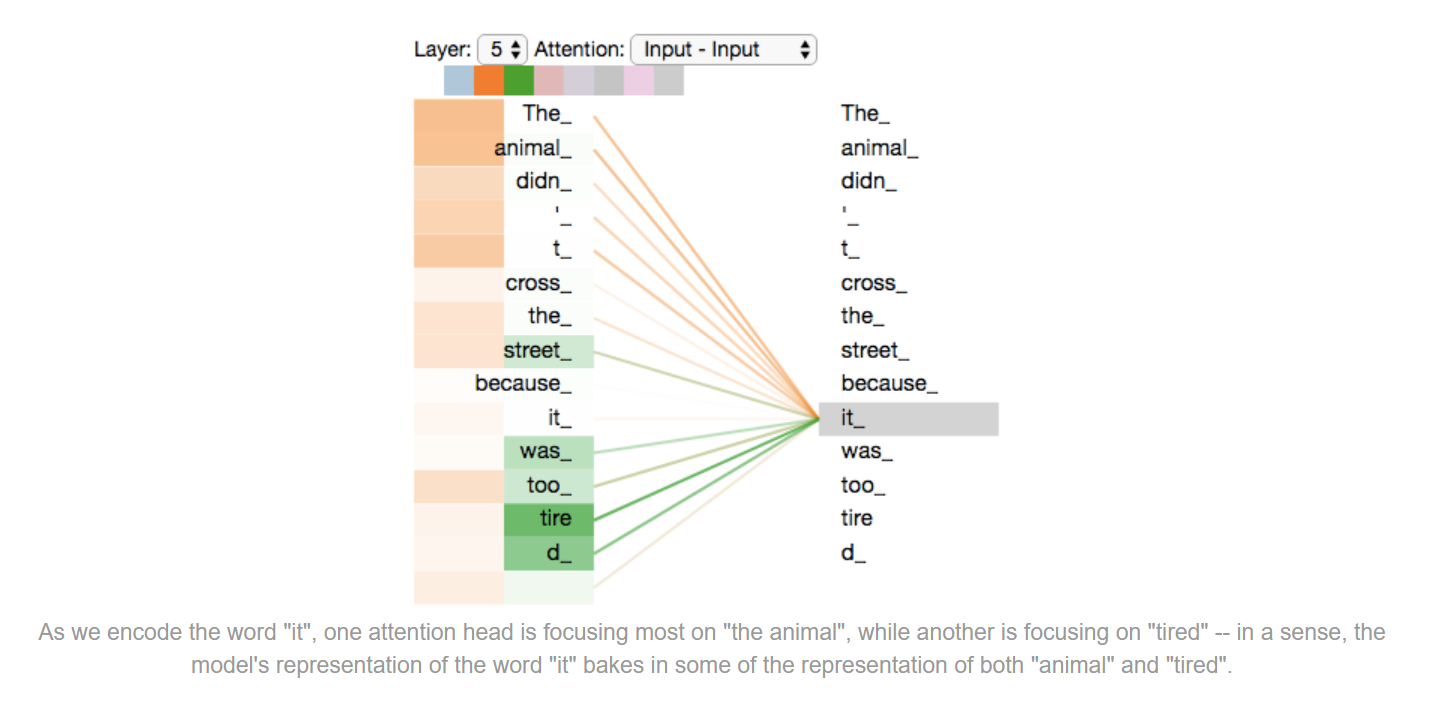
因此，总结一下多头自注意力机制的优点与作用，大概有以下两点：

能捕捉更多位置的信息，避免信息过于集中和忽略其他信息的问题。
每个注意力头都提供了一个独立的表示子空间。这种机制使得每个头可以专注于输入中的不同特征或模式。例如，一个注意力头可能会专注于捕捉词汇之间的语法关系（如主谓宾结构），另一个可能会专注于捕捉词汇之间的语义关系（如同义词或指代关系）。通过并行计算多个子空间的注意力，模型可以更全面地理解输入信息，而不是局限于单一的关系表示。

而encoder就是用8层这种多头自注意力机制的单元堆叠而成。每一个encoder的输出，作为下一层多头的QKV输入。因此，encoder的每个位置都可以注意到之前一层encoder的所有位置。

到这里，我们完成了encoder的multi-head attention部分。

这里我们注意一下，自始至终词与词之间的顺序好像没发挥作用。如下图：

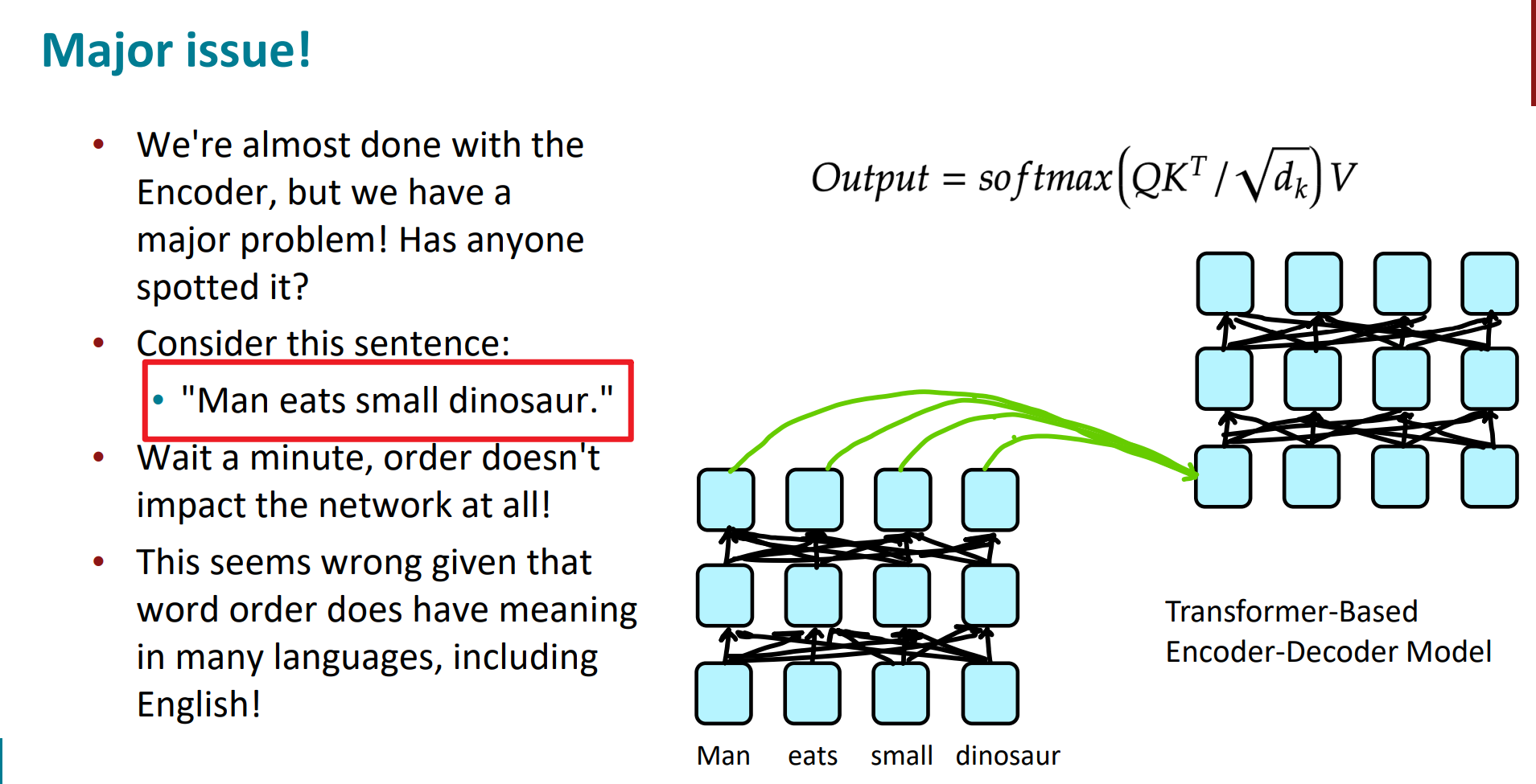
在 Transformer 模型中，自注意力层的计算是基于输入序列中所有位置的关系进行的，这意味着模型在计算时不依赖于输入的顺序。为了弥补这一点，必须为输入中的每个元素提供一个额外的信息，以标识它在序列中的位置。这就是位置编码的核心任务。

我们看transformer的模型示意图发现，在encoder和decoder输入的时候，都加入了positional encoding，即位置编码信息。我们就来看一下是如何把词与词之间的顺序关系加入进来的。

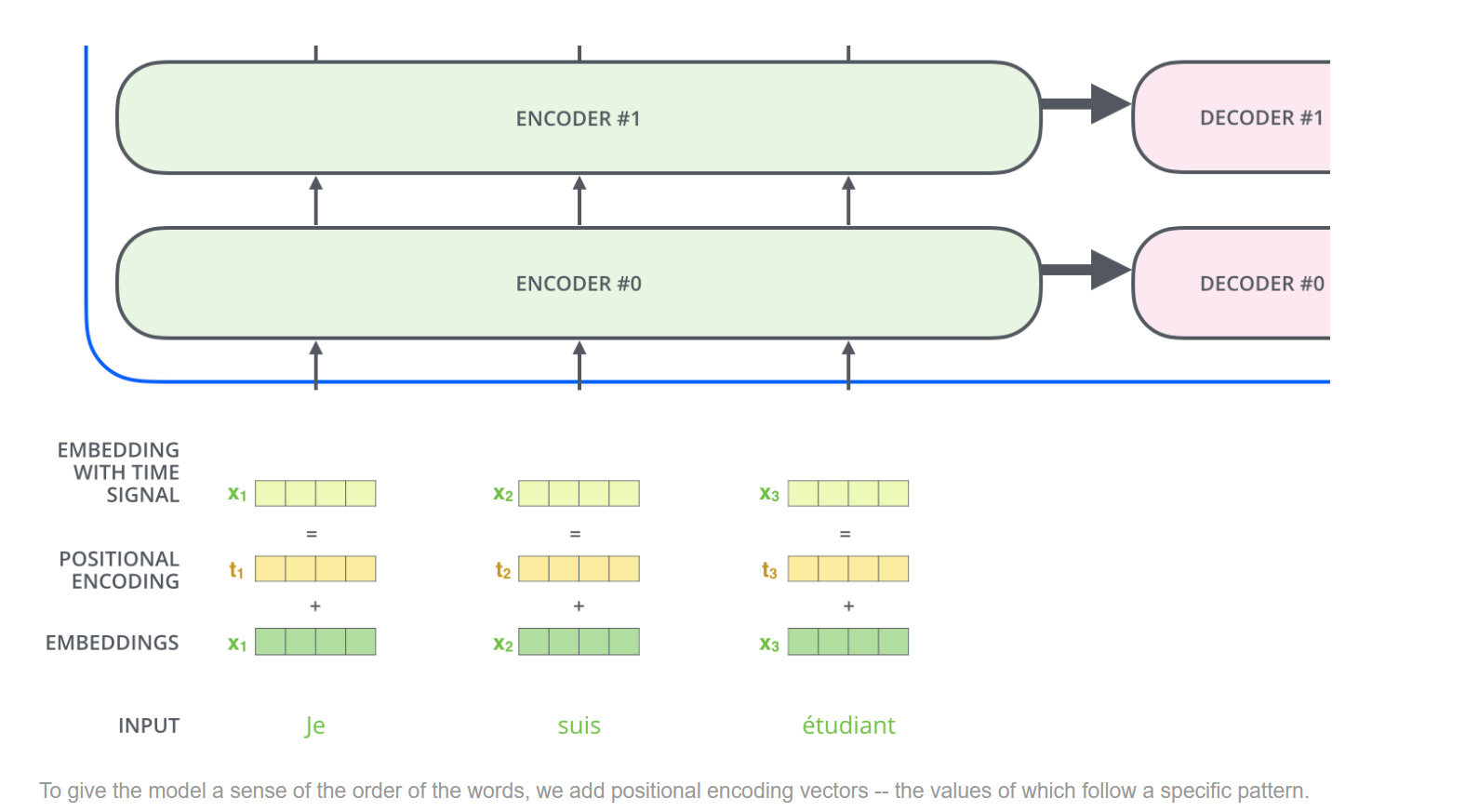
那么我们以4维度为例，看一下positional encodings的运行机制。

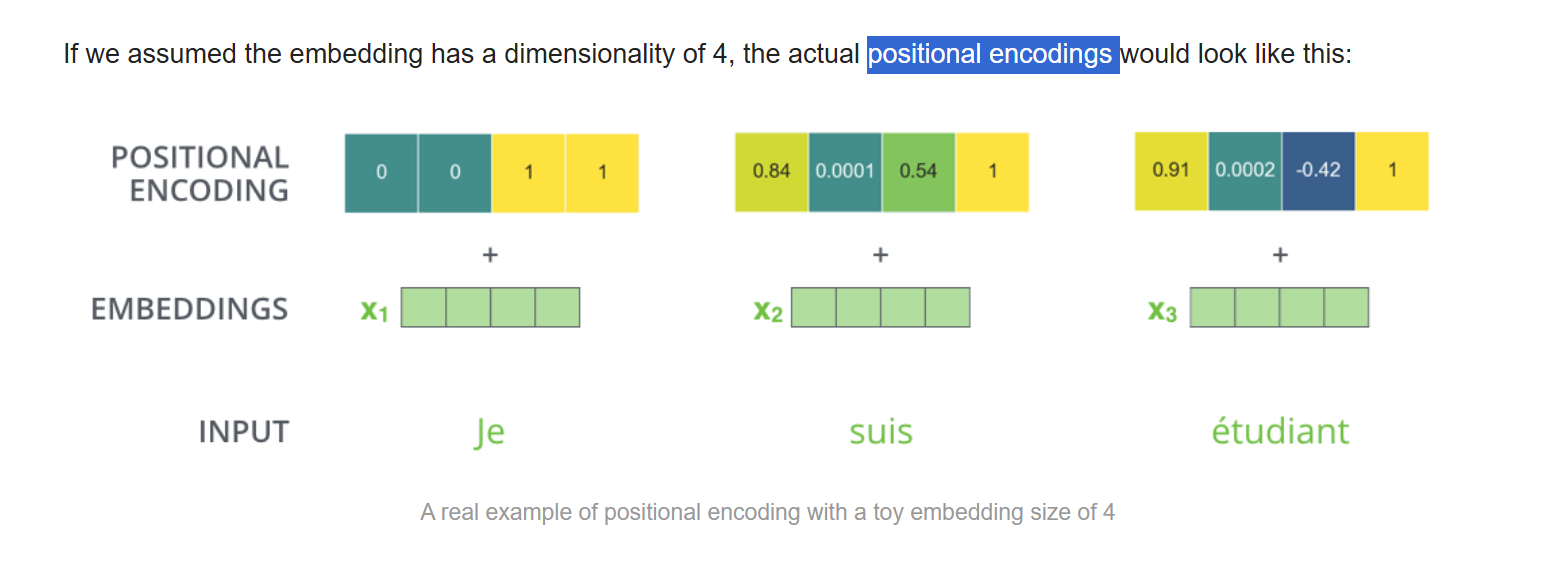
我们将位置编码可视化一下，如下图：

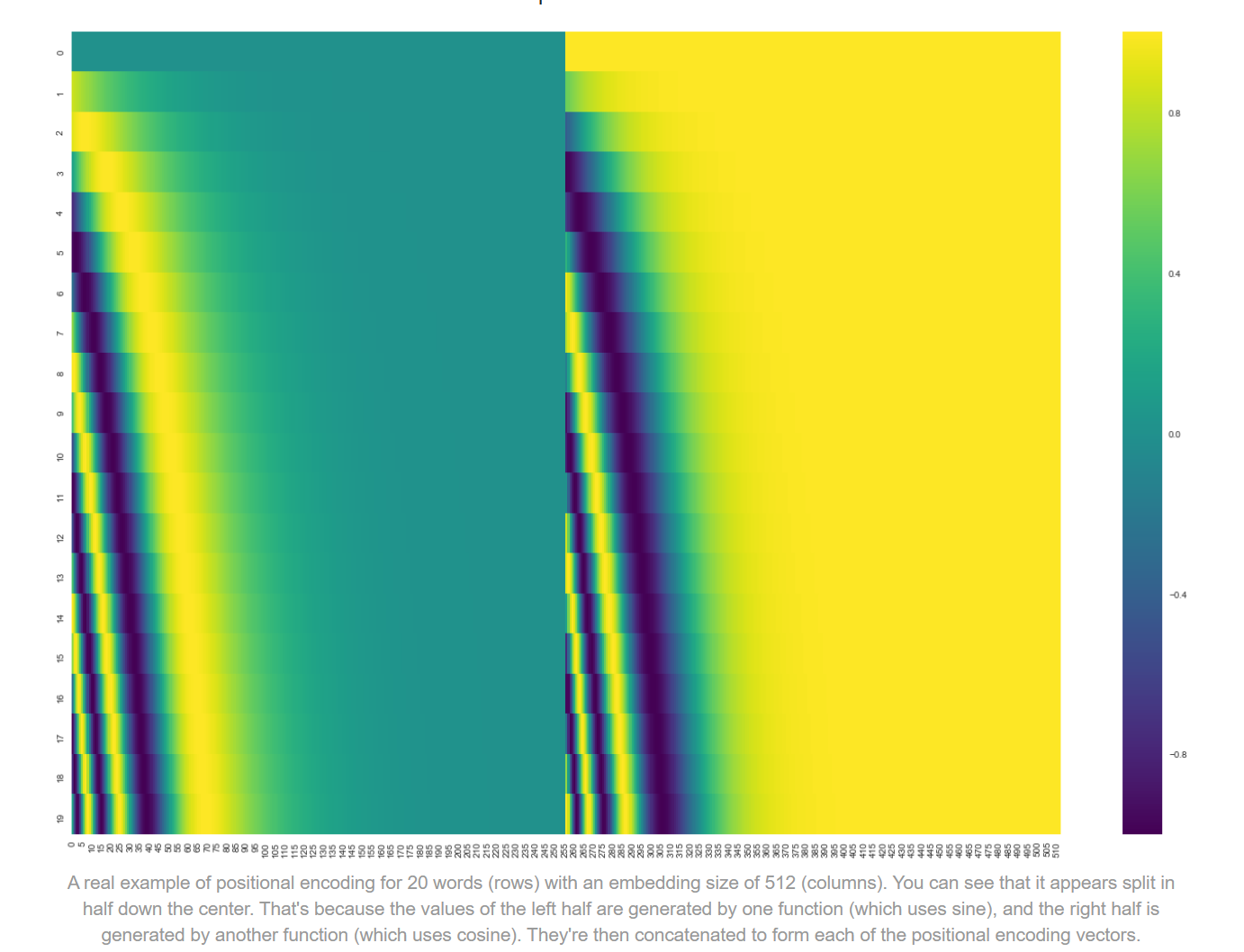
我们可以看到，这是一个20*512的图。20代表input有20个word，每一个word用512维度的向量表示。每一行代表一个word的表示，第一行是第一个word。

我们注意到，好像在中间形成了两块的分割线。这是因为左边的函数是sine，右边是cosine形成的，然后将二者进行拼接。

$$\begin{gathered} \mathrm{PE}_{(pos,2i)}=\sin\left(\frac{pos}{10000^{2i/d_{\mathrm{model}}}}\right) \\ \mathrm{PE}_{(pos,2i+1)}=\cos\left(\frac{pos}{10000^{2i/d_{\mathrm{model}}}}\right) \end{gathered}$$

我们结合具体代码看一下：

def get_angles(pos, i, d_model):
  angle_rates = 1 / np.power(10000, (2 * (i//2)) / np.float32(d_model))
  return pos * angle_rates

这段代码很清晰，就是实现公式的表示。

之后我们注意到公式是要求，奇数位置用cosine，偶数部分用sine。

def positional_encoding(position, d_model):
  angle_rads = get_angles(np.arange(position)[:, np.newaxis],
                          np.arange(d_model)[np.newaxis, :],
                          d_model)

  # apply sin to even indices in the array; 2i
  angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])

  # apply cos to odd indices in the array; 2i+1
  angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])

  pos_encoding = angle_rads[np.newaxis, ...]

  return pos_encoding

这是原文章的实现思路。这样的位置编码可视化情况就不像上图那样在中间部分很清晰的分开，而是一种交织穿插的感觉。

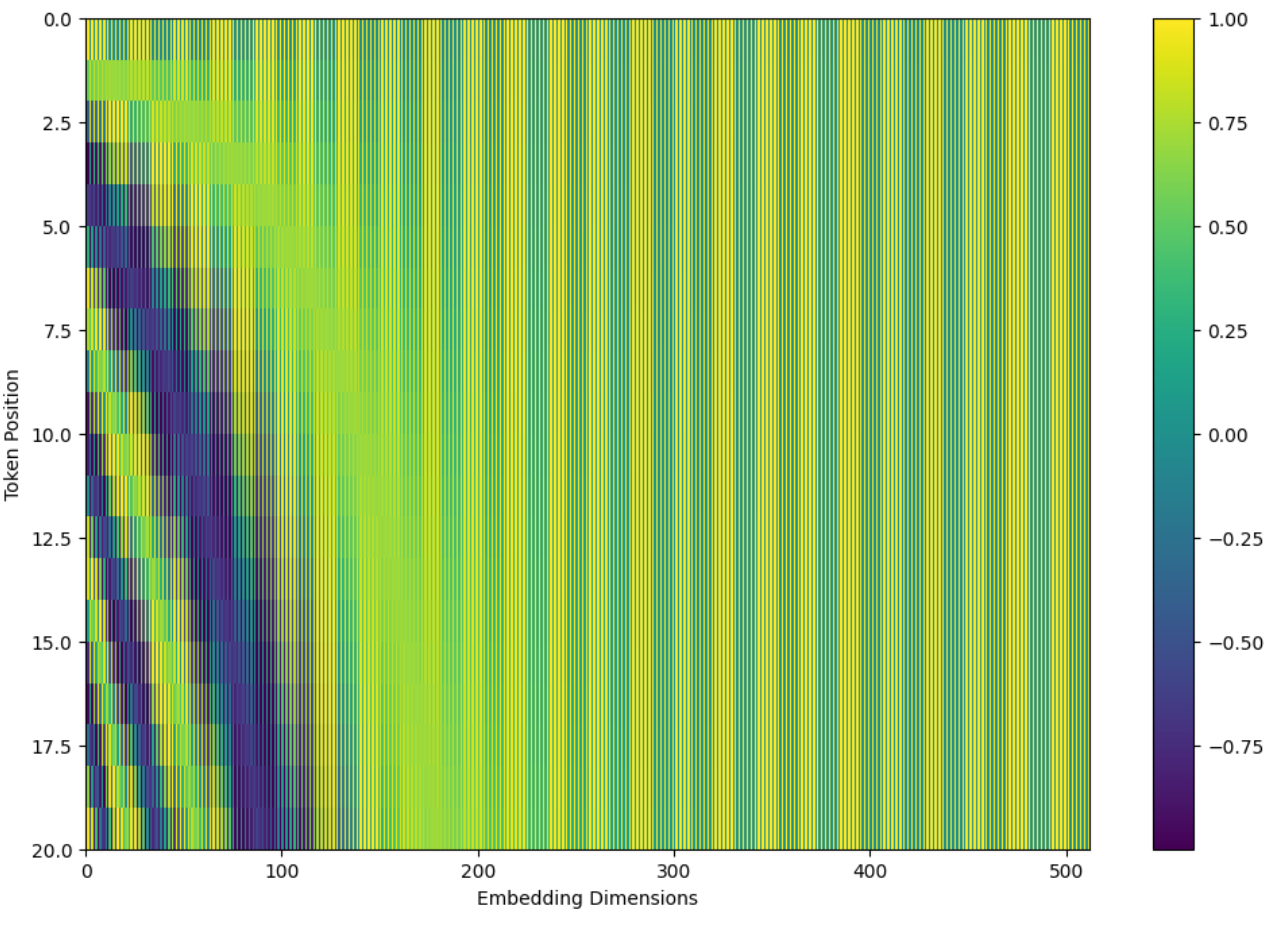
到这里，我们就完成了位置编码部分的理解。

接着看transformer的架构图，该到Add&Norm，也就是残差连接和归一化的模块了。

我们注意到，在encoder部分：模型在完成向量化表示（embedding和positional encoding后）和self-attention的时候，有一个残差连接与归一化；在进入FFNN的时候，又有一次残差连接与归一化。

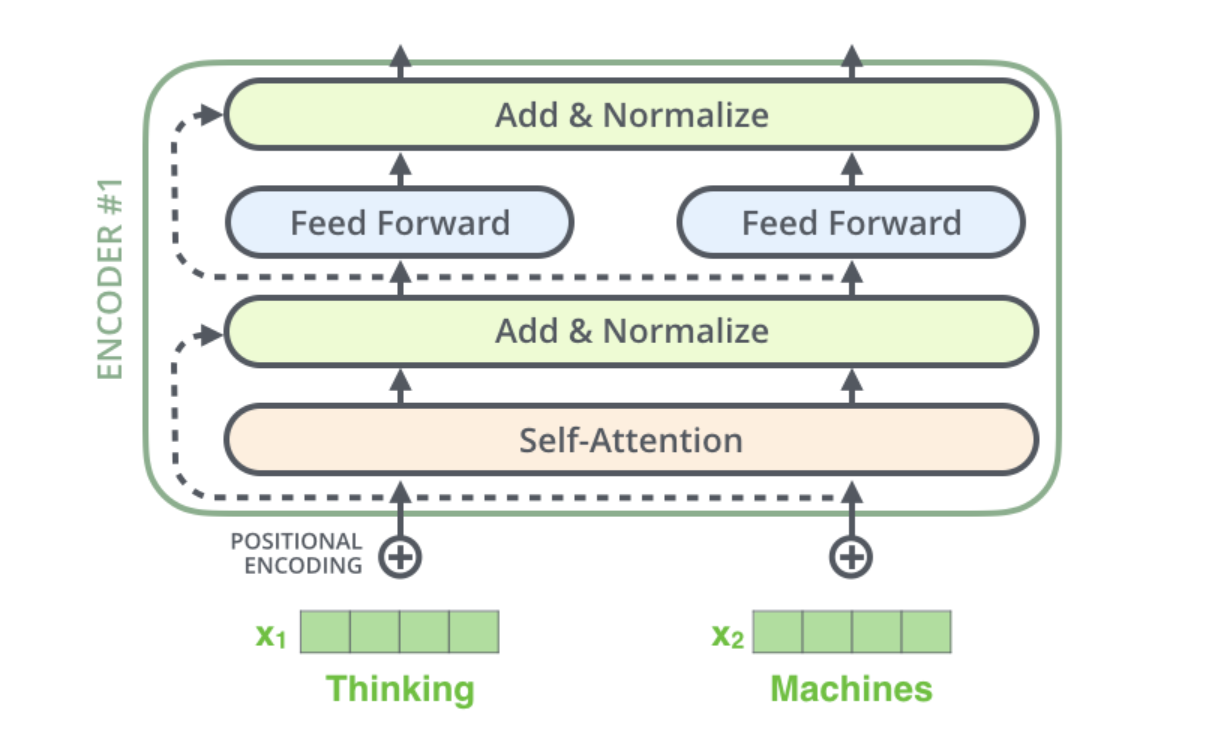
我们单独再可视化一下positional encoding和self-attention的那个Add&Norm：

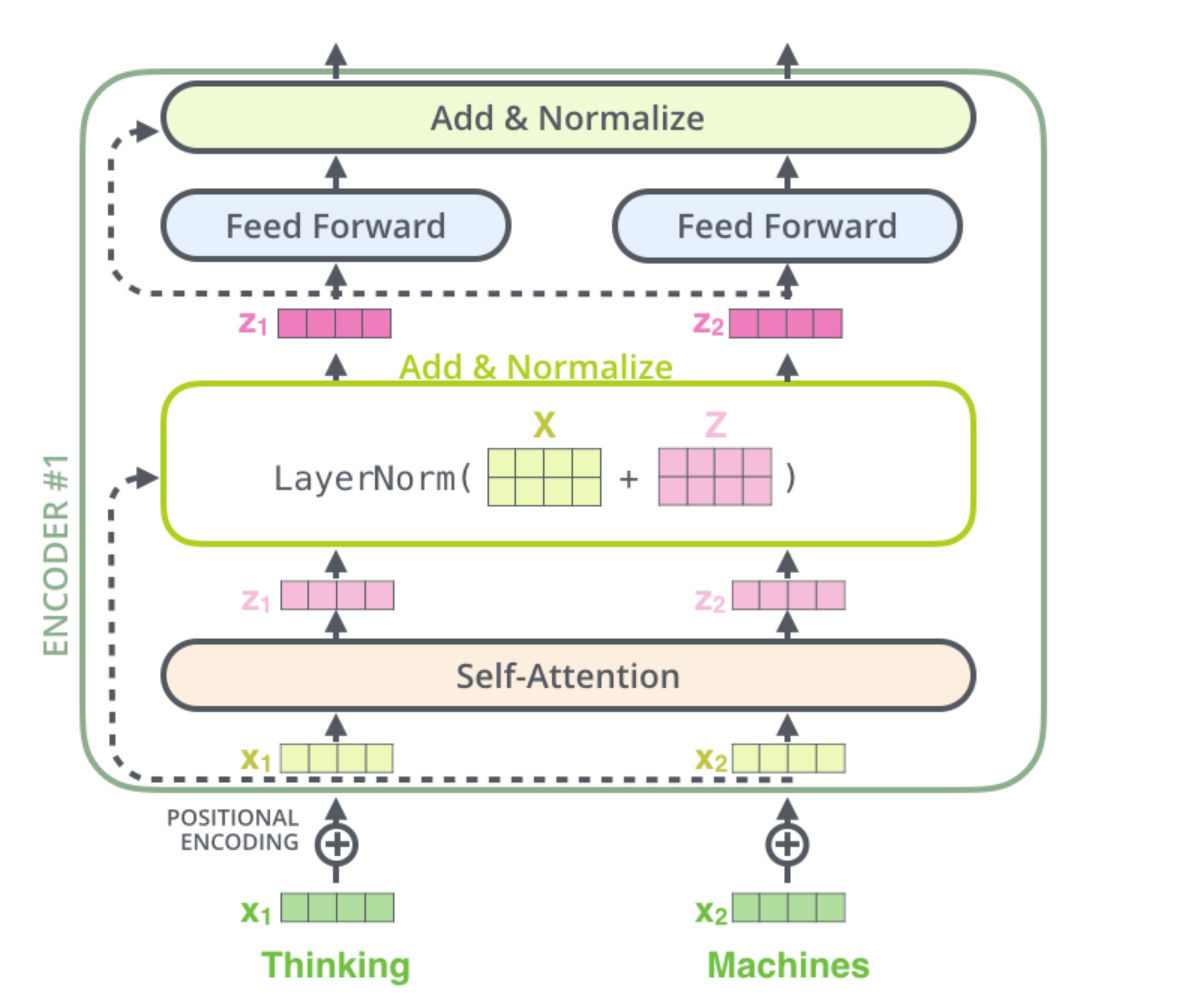
这里我们假设transformer就是由两层encoder和两层decoder组成。那我们就可以清晰画出模型结构示意图，尤其注意模块之间的数据流动方向和位置。

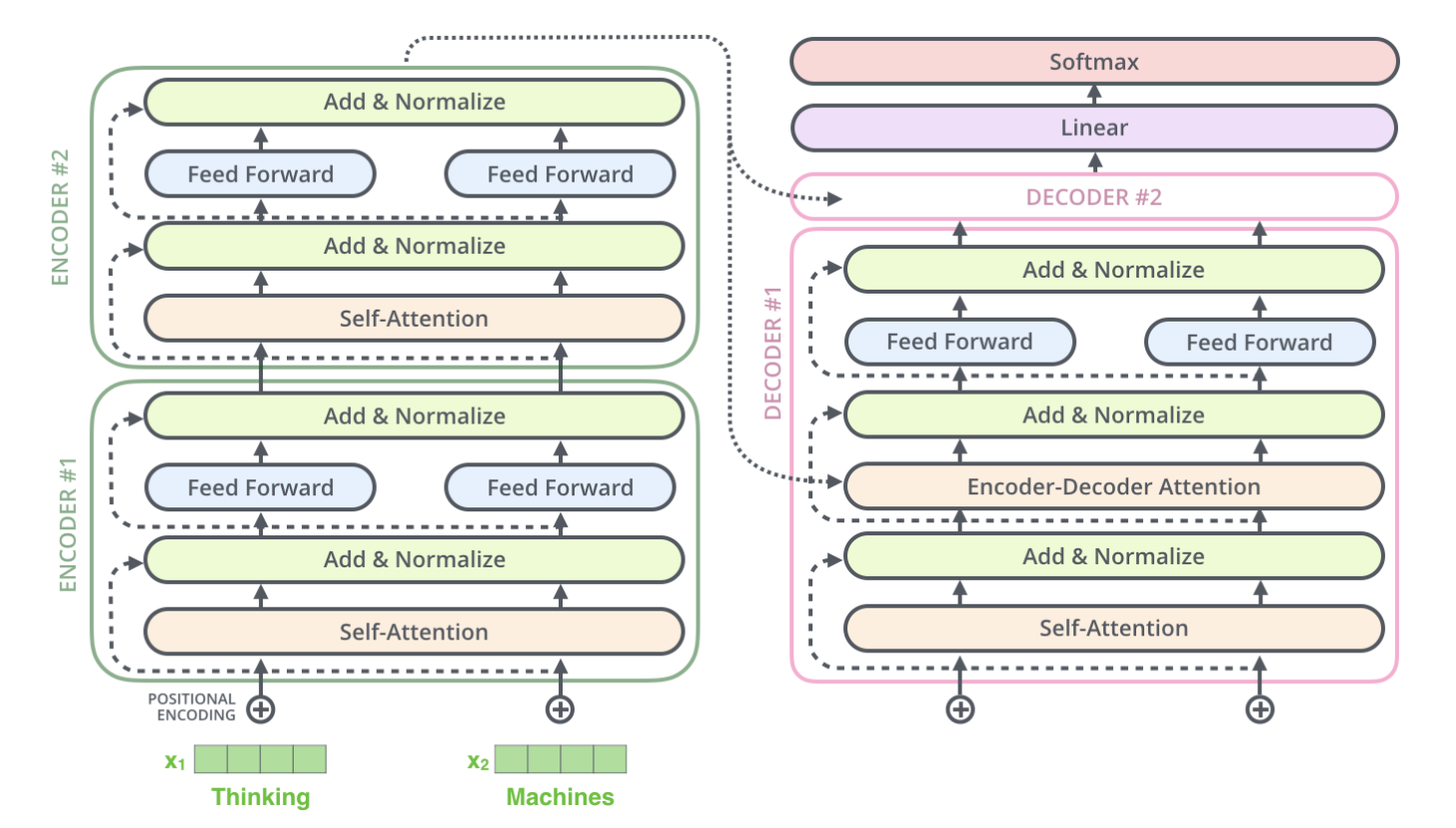
我们可以看到，第二个encoder的输出，即Add&Norm后的数据，有两个移动方向。
1. 指向了第一个decoder的encoder-decoder attention模块，这其实对应着decoder的第二个muti-head attention（第一个是mask-multi-head attention）
2. 指向了第二个decoder的输入。

这就和经典的那个transformer模型对应上了（红框部分）

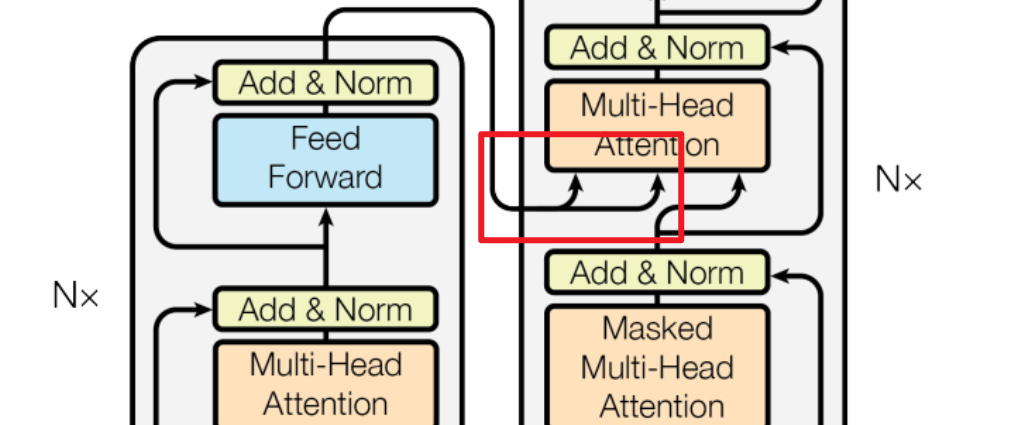
那么知道了Add&Norm在模型结构中的整体位置和作用以及数据流动情况，我们就单独看一下这两块是什么即可。其实也都是常见的组成部分。

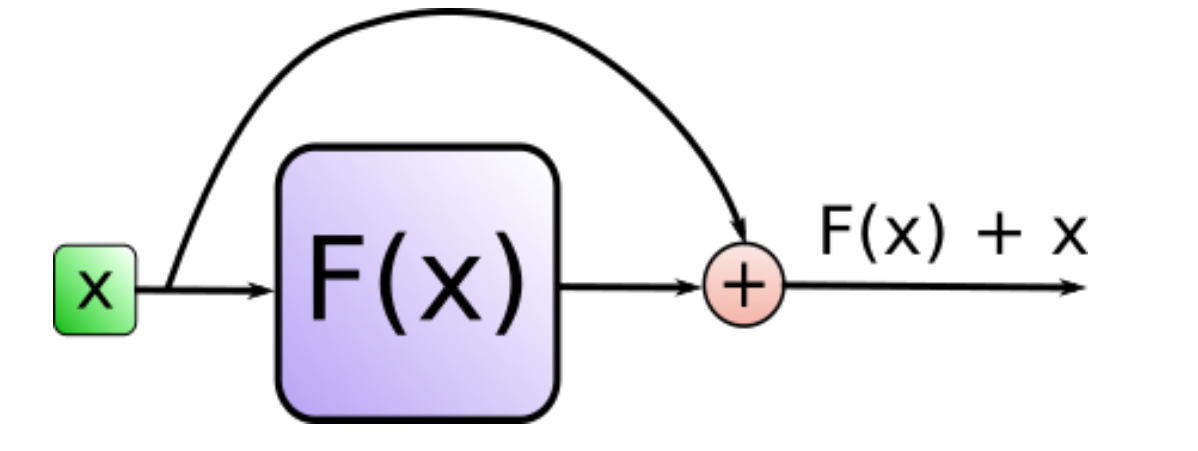
Add就是残差连接部分，也就是Residual Connection。经典的鼎鼎大名的就是何恺明的ResNet。作用如下：

是为了解决多层神经网络训练困难的问题，通过将前一层的信息无差的传递到下一层，可以有效的仅关注差异部分，这一方法之前在图像处理结构如ResNet等中常常用到。

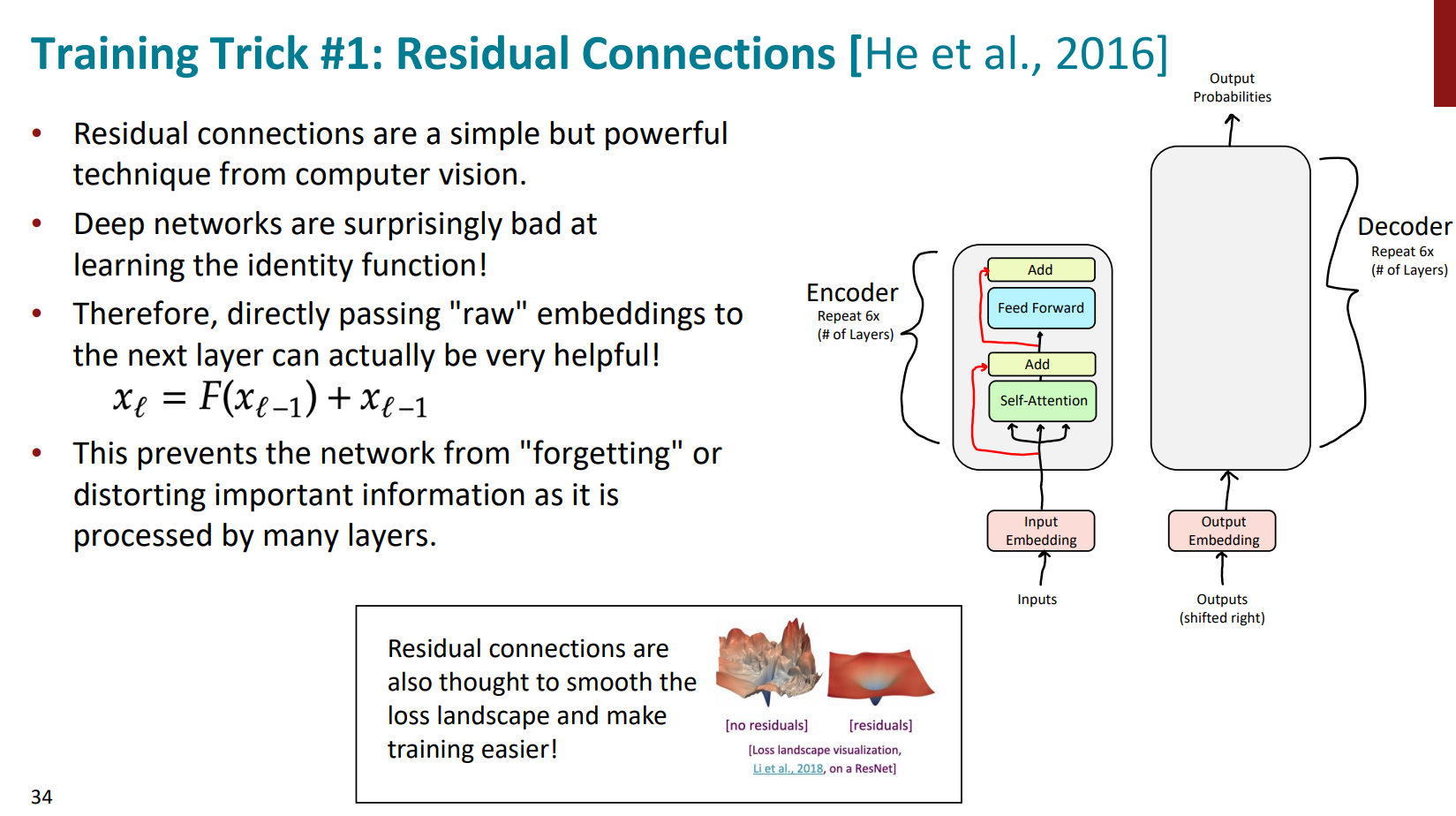
Norm就是归一化，文章用的Layer Normalization，没用Batch Normalization。

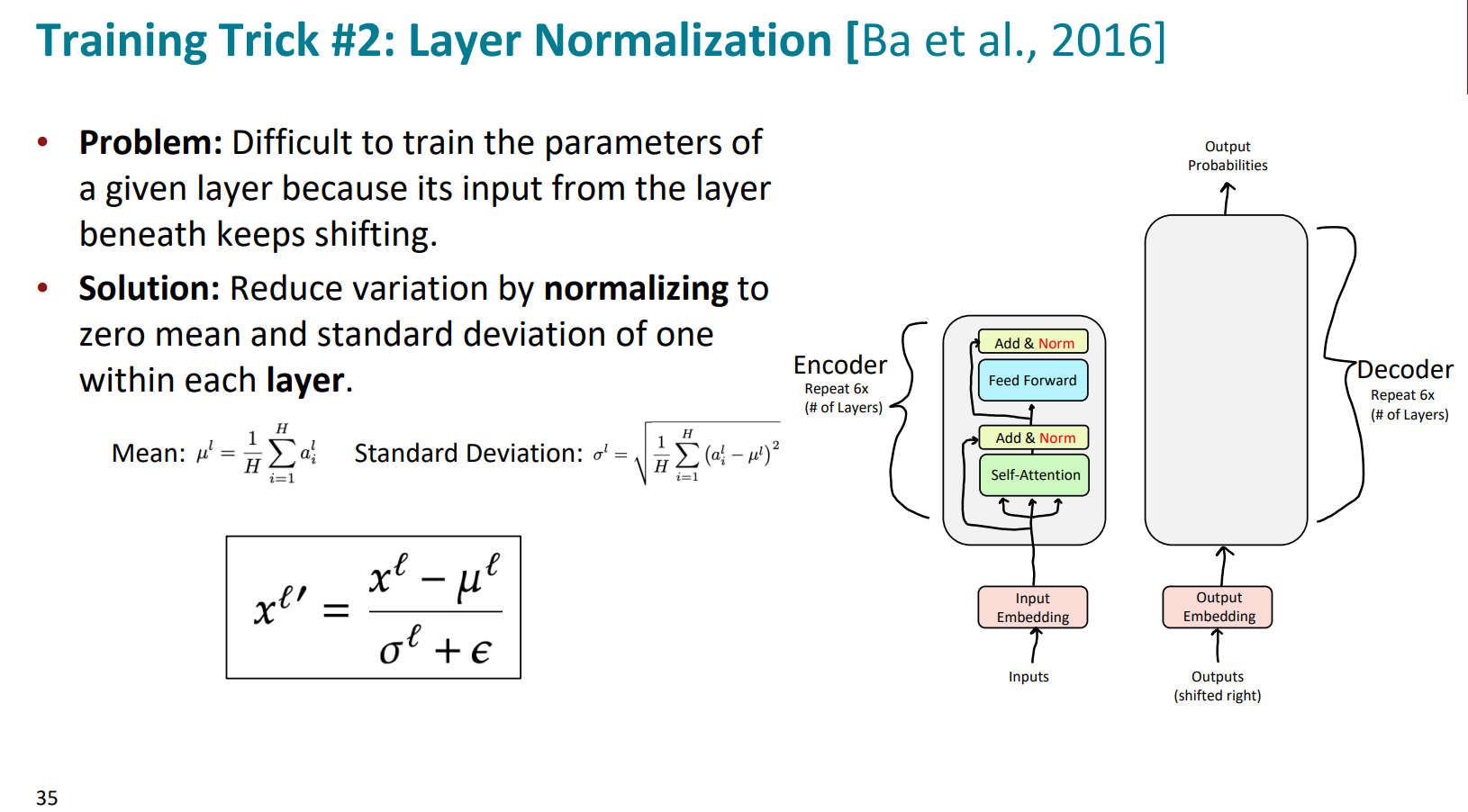
这里我们不再详细去探讨为什么transformer不用batch而是用layer。在之后的文章会单独去谈论研究。但二者的特点一句话就可以概括：

BatchNorm是对一个batch-size样本内的每个特征[分别]做归一化，LayerNorm是[分别]对每个样本的所有特征做归一化。

因此，下面这个图以3个sample为例，很直观形象展示了layer normalization的过程。很重要的一句话就是：

normalization across features independently for each sample。

到这里，encoder部分就全部完成了，接下来我们搞一下decoder。

其实decoder的组成部分和encoder非常类似，结构也类似，当然也有区别。我们在论述decoder的时候，相同部分就不再赘述，而是重点说decoder特有的部分和encoder-decoder的协同工作。

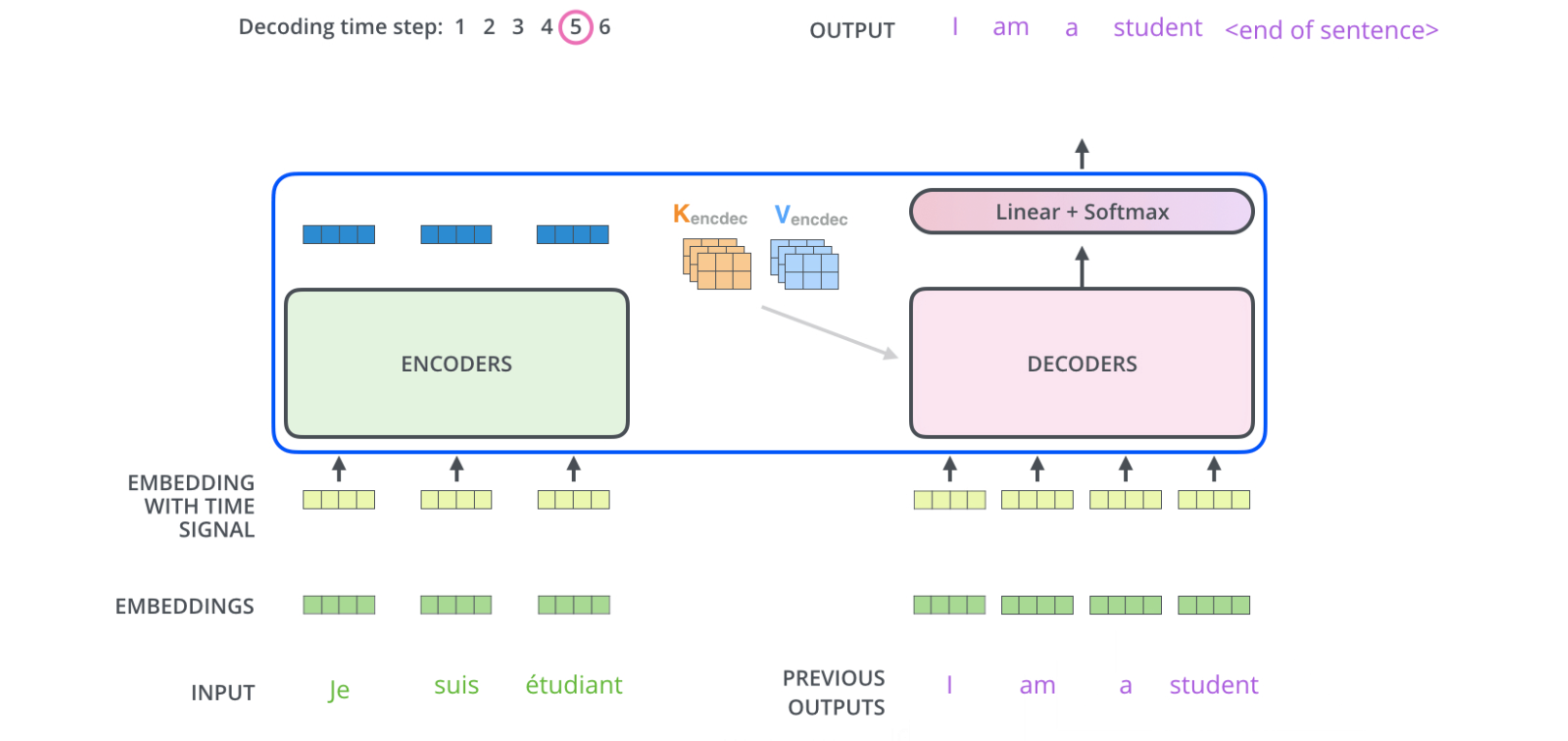
第一个encoder很重要的任务是处理input sequence，最后一个top encoder则是将输出处理转化为K何V，传递到每一个decoder的encoder-decoder的attention部分。目的是帮助每一个decoder去专注到input的合适的部分。

以机器翻译的任务为例可以完美展示下面的encoder-decoder部分。假设共有6个step，每一个step的最后一个decoder输出对应位置的翻译结果。

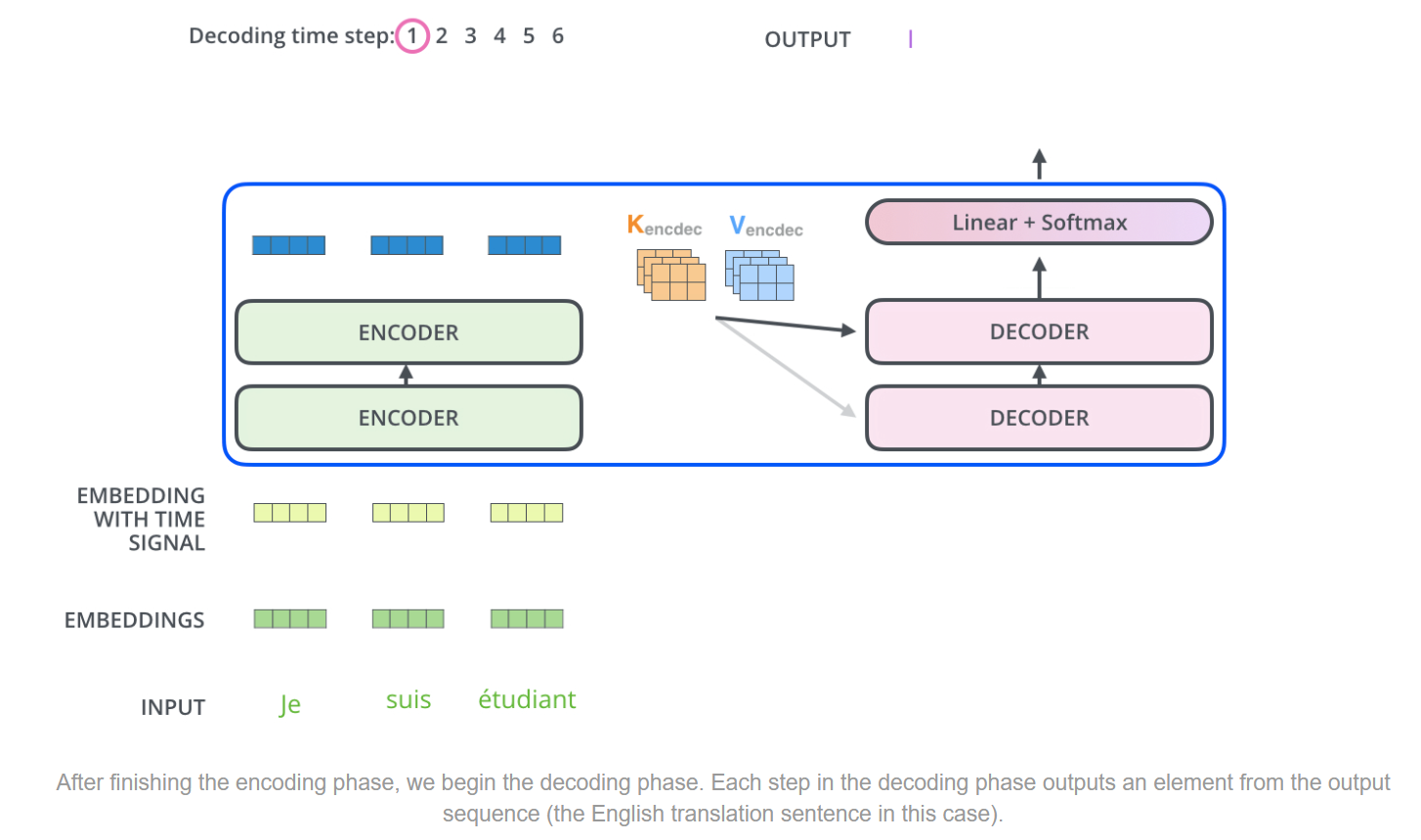
decoder的运行机制也和encoder类似：
1. 每一次完整step的output都作为下一次step的decoder的input。
2. 同样对decoder的input也进行embedding和positional encoding，加入位置信息。
3. 直到模型输出特殊符号来表示已经输出完毕，decoder才输出停止。

接下来我们看一下decoder的特殊点（即和encoder不同的地方）

第一个很重要的不同点：decoder的第一个attention是mask-multi-attention。

encoder的attention机制是当前位置的word可以和所有位置的word进行attend。

但encoder的时候，每次只生成序列中的一个word，模型在预测当前单词（如 “chef”）时不应该看到未来单词（如 “who”），否则会导致数据泄漏。

原因就是翻译的时候，按道理说模型是无法看到后面的词的。

In the decoder, the self-attention layer is only allowed to attend to earlier positions in the output sequence. This is done by masking future positions (setting them to -inf) before the softmax step in the self-attention calculation.

因此，我们在decoder的目标是：确保decoder仅能基于当前和之前的词语进行预测，而不能看到后续的词语。

要想解决这个问题，可以动态调整attention中的K和V（当前位置是Q），即每个时间步单独生成 keys 和 queries，仅包含当前及之前的词语。但这样看似解决了，缺点是无法并行计算，效率低下。

另一个效率比较高的解决办法，也就是文章提出的mask方法：

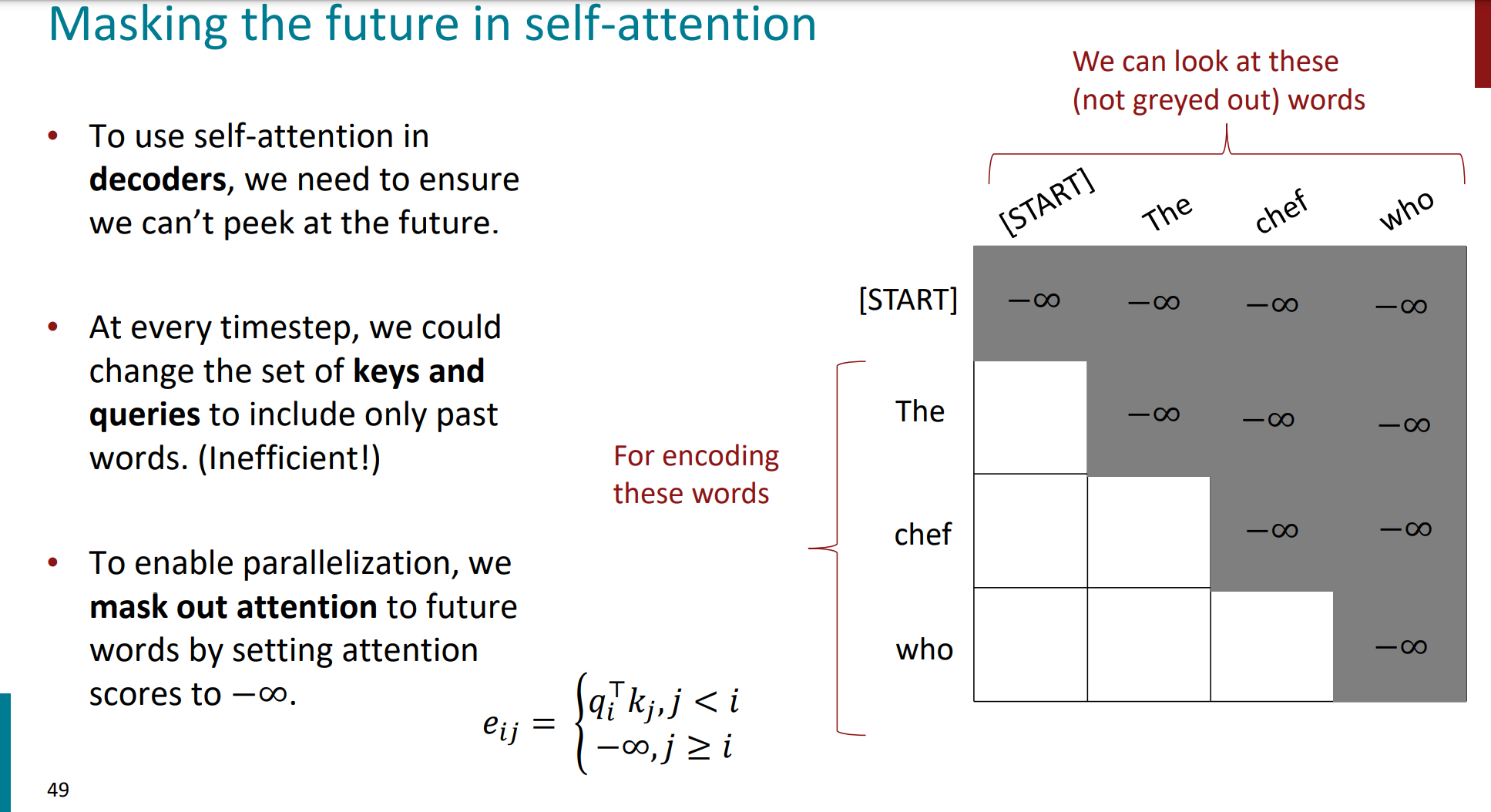
在右侧的灰色矩阵中，构造了一个上三角矩阵。

$$e_{ij}=\begin{cases}q_i^\top k_j&j\leq i\\-\infty&j>i\end{cases}$$

这样的效果是：

当前位置（i）是q，j是作为k和v。当$j>i$的时候，注意力分数被设置为$-\infty $。这样的话，我们后面softmax的时候，$-\infty$会被归一化为0，也就消除了后面词的影响。

白色部分表示decoder可以注意到的词语（包括当前词和之前的词）。
灰色部分表示被mask的区域（即未来词）。
每一行对应一个时间步，随着时间的推移，模型能看到的词逐渐增加。

在预测 “chef” 时，模型只能看到 “[START]” 和 “The”。
在预测 “who” 时，模型可以看到 “[START]”、”The” 和 “chef”。

这样的好处就是一次性可以完成整个sequence的mask计算，并行化高，效率上来了。

这里详细说一下为什么这样并行化效率高：

我们知道，attention都是基于矩阵计算的，mask attention的计算过程如下：

$$\mathrm{Attention}(Q,K,V)=\mathrm{Softmax}\left(\frac{QK^\top}{\sqrt{d_k}}+\mathrm{Mask}\right)V$$

所以整个步骤如下：（正好回忆一下hh）

$QK^{\top}$：点积操作，生成所有词之间的相关性分数矩阵（大小为$T \times T$，$T$是序列长度）、
加上mask矩阵：通过矩阵加法一步完成所有时间步的mask操作。
Softmax 归一化：计算注意力权重，同样可以在矩阵维度上并行处理。
权重与$V$的加权求和：矩阵乘法直接完成。

此时的mask矩阵如下所示：

$$\text{Mask}=\begin{bmatrix}0&-\infty&-\infty&\ldots&-\infty\\0&0&-\infty&\ldots&-\infty\\0&0&0&\ldots&-\infty\\\vdots&\vdots&\vdots&\ddots&-\infty\\0&0&0&\ldots&0\end{bmatrix}$$

每一行代表当前时间步能访问的词。
mask矩阵通过一次加法，将未来时间步的注意力分数全部屏蔽，而无需为每个时间步单独计算。

接下来的encoder-decoder的attention是普通的multi-head attention。只不过Q是来自上一层的decoder，K和V是来自最后一个encoder的（6层encoder全部计算完成后的）。使得decoder的每一个位置都可以attend到输入序列的每一个位置。

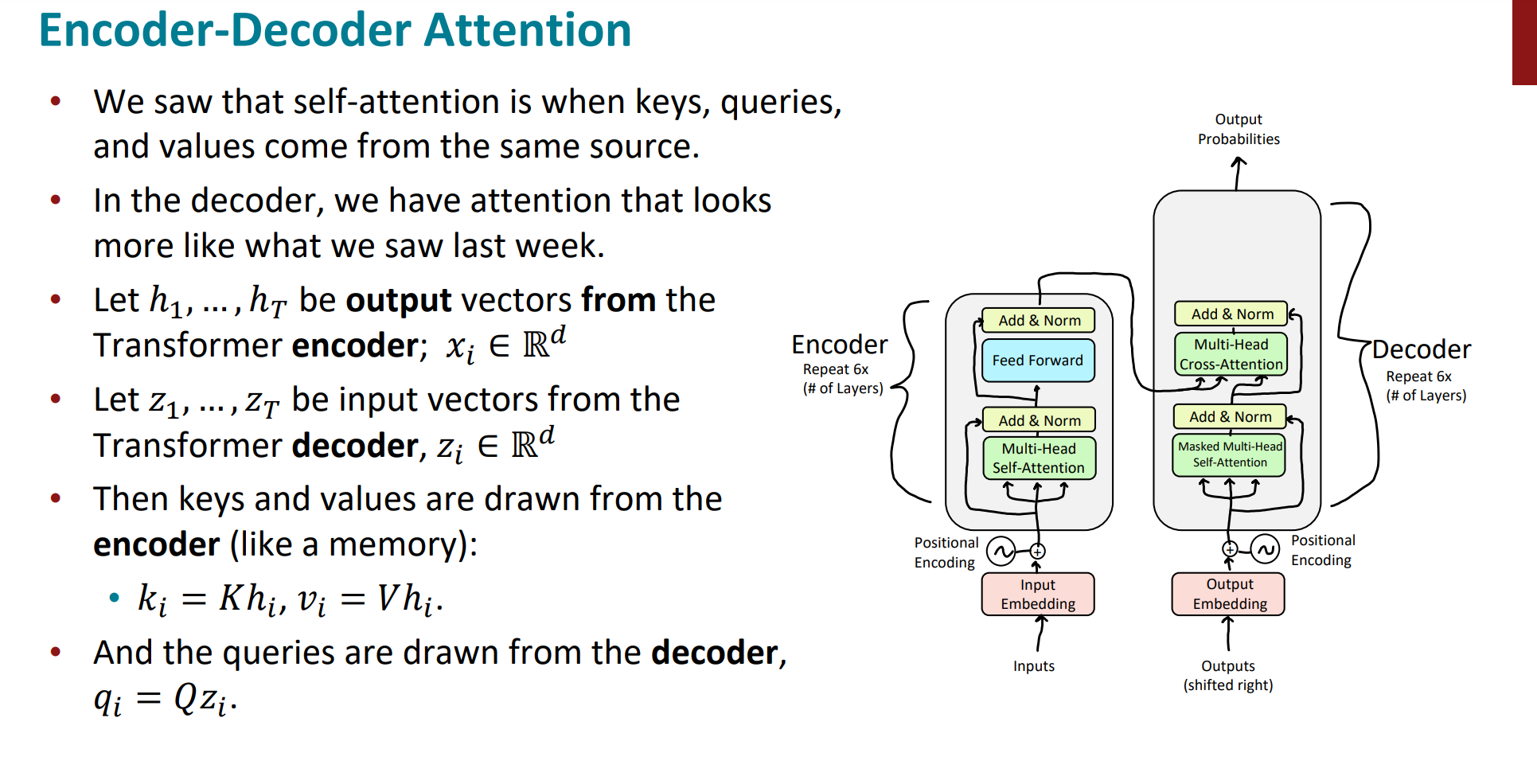
总结一下，k和v的来源总是相同的，q在encoder及第一级decoder中与k,v来源相同，都是来自上一层的decoder；在encoder-decoder attention layer中q与k,v来源不同，其中q是来自上一层decoder的输出，K和V是来自最后一层encoder的输出。

到这里，decoder的核心模块也完成了。

我们发现，就剩下decoder中的Linear和softmax层的模块了。接下来我们就来看一下这两部分。

最后一层decoder的输出向量本质上只是一个数值表示，无法直接对应到词语，我们要想输出word sentence的话，需要进一步映射。这时候线性层的重要性就来了。

Linear层就是一个简单的全连接层，将解码器堆栈输出的固定维度向量（如 512 维）投影到一个更大的空间，一般就是词汇表大小（vocab_size）。然后再跟一个softmax层，得到每个word的输出概率分布，这时候此time step的输出word就可以确定了，即选择概率最大的那个word作为output。

下面这张图会更清晰展示上面说的这个过程。

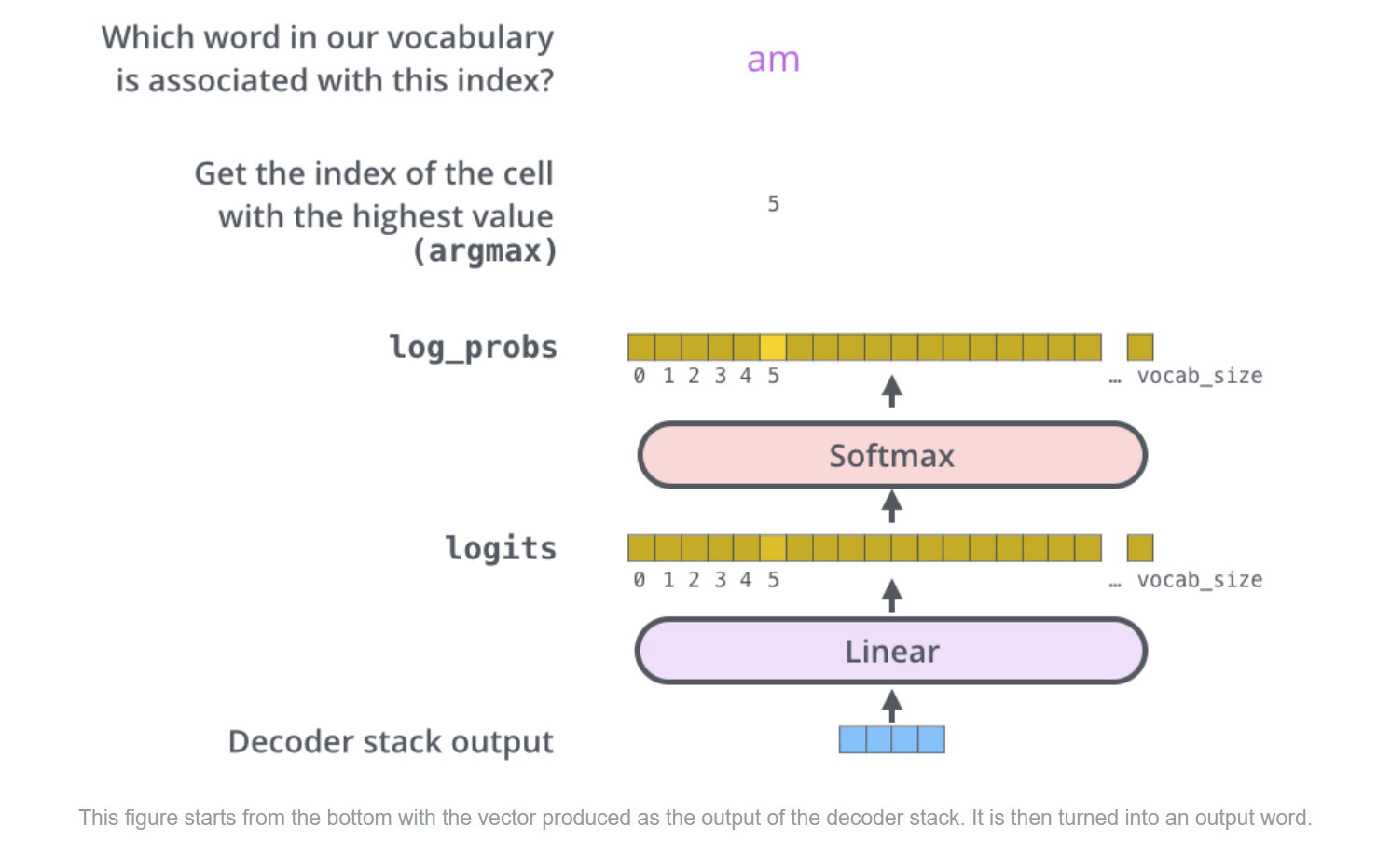
结合这个图我们再过一遍（虽然有些啰嗦，但感觉捋清楚还是很舒服的hh）

stack decoder的输出作为linear的输入。
linear将低维度的向量（512）映射为高维度的向量（一般是词表大小vocab_size），得到每个word的得分情况的一个logits向量。
将logits过一个softmax进行归一化（全部正数且和为1）
选择概率最大的index对应的word作为当前time step的输出。

至此，我们完成了decoder的全部模块。

我们完成了encoder和decoder这两个transformer中的核心组成部件。

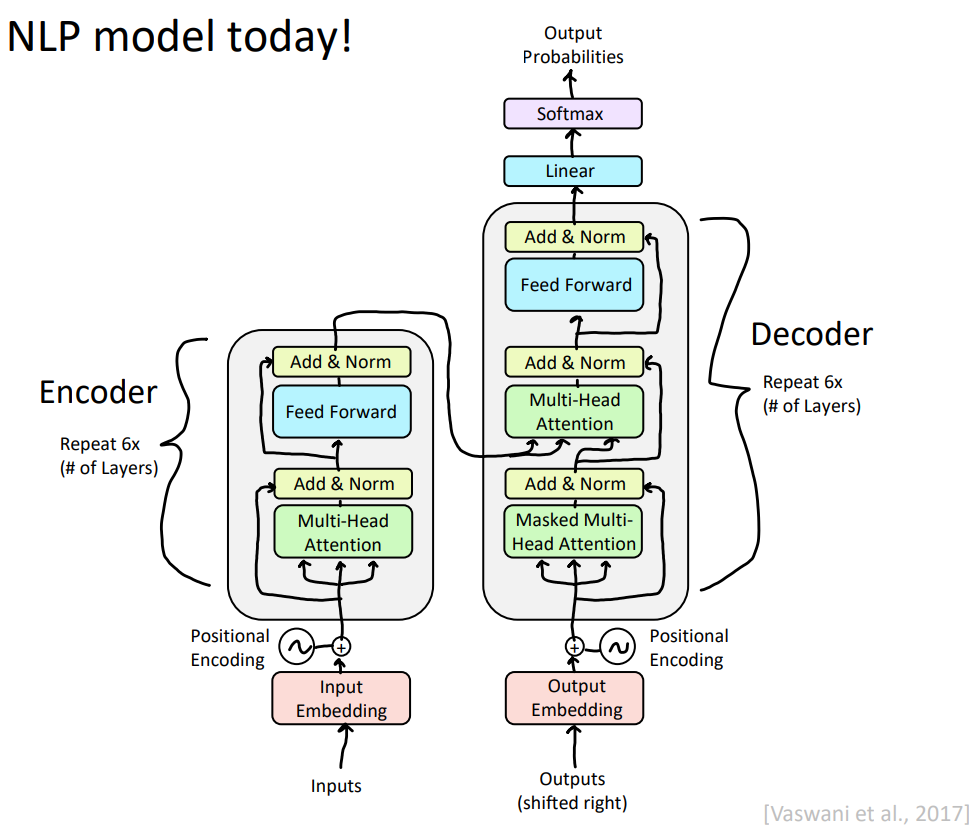
这时候我们闭上眼睛，去回顾那张经典的transformer模型架构图。（睁开眼睛就是下面的感觉）

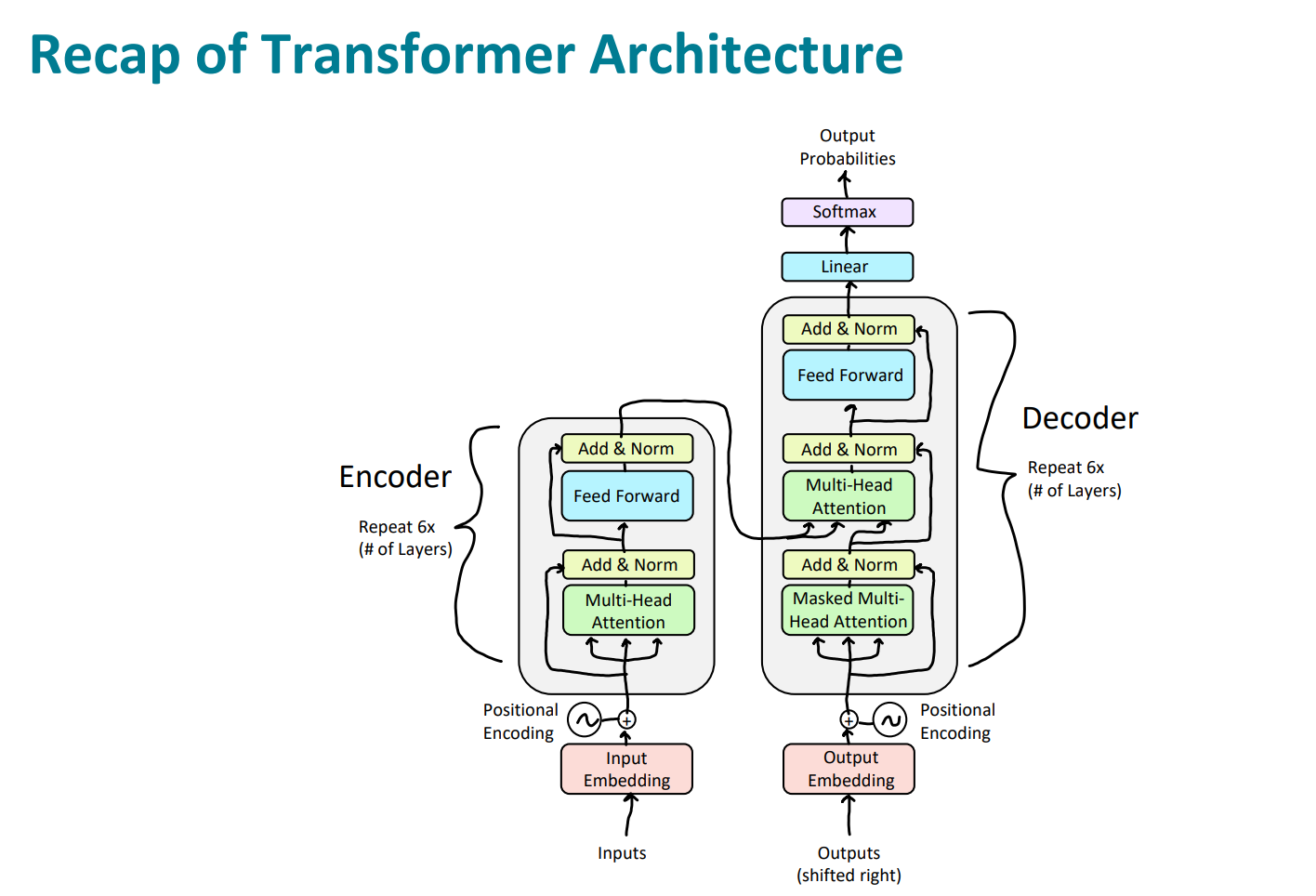
接下来，我们去看一下整个的训练过程的细节。

因为我们做的是有监督（即带标签的dataset），所以可以compare its output with the actual correct output.

我们举个具体的例子贯穿训练过程，这样可以更形象一些。

假设词汇表vocabulary中只有6个词：

“a”, “am”, “i”, “thanks”, “student”,  “<eos>”

那么接着我们就可以用one-hot进行编码了（在encoder开始的时候就word embedding）

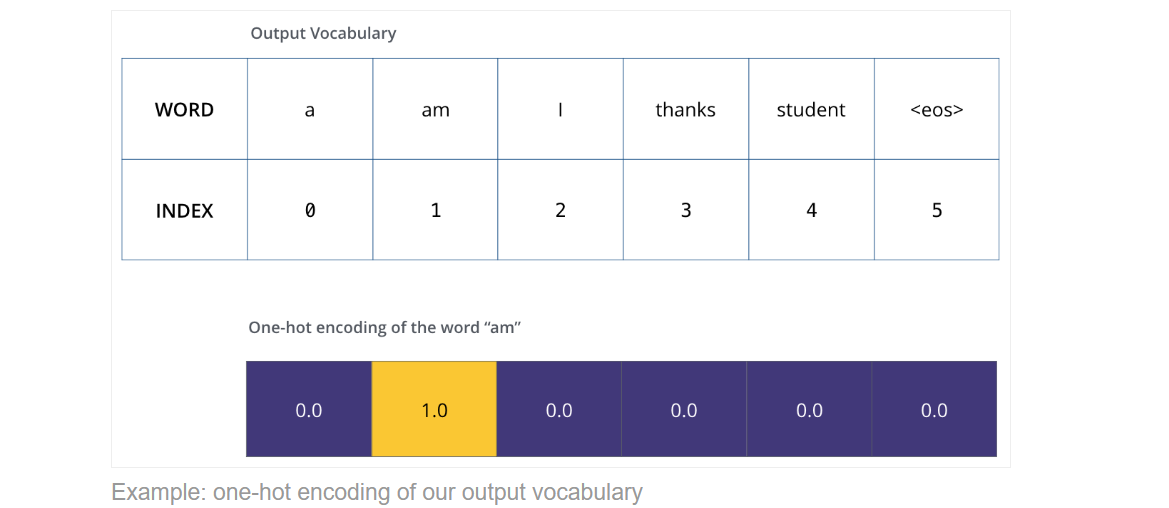
那么word representation解决了，我们就看一下loss function。

我们是希望对比两个概率分布的，那么经典的损失函数就是交叉熵cross entropy。

以输出“thanks”为例，我们希望未经训练的model（因为是随机初始化参数）的概率分布与正确的期望的概率分布进行靠拢，这里用交叉熵和反向传播即可实现。

当然具体对比的时候，我们不可能一个word一个word去实现，而是以sentence为单位去对比概率分布。但思路也是让sentence中每个word的位置都达到目标的输出。

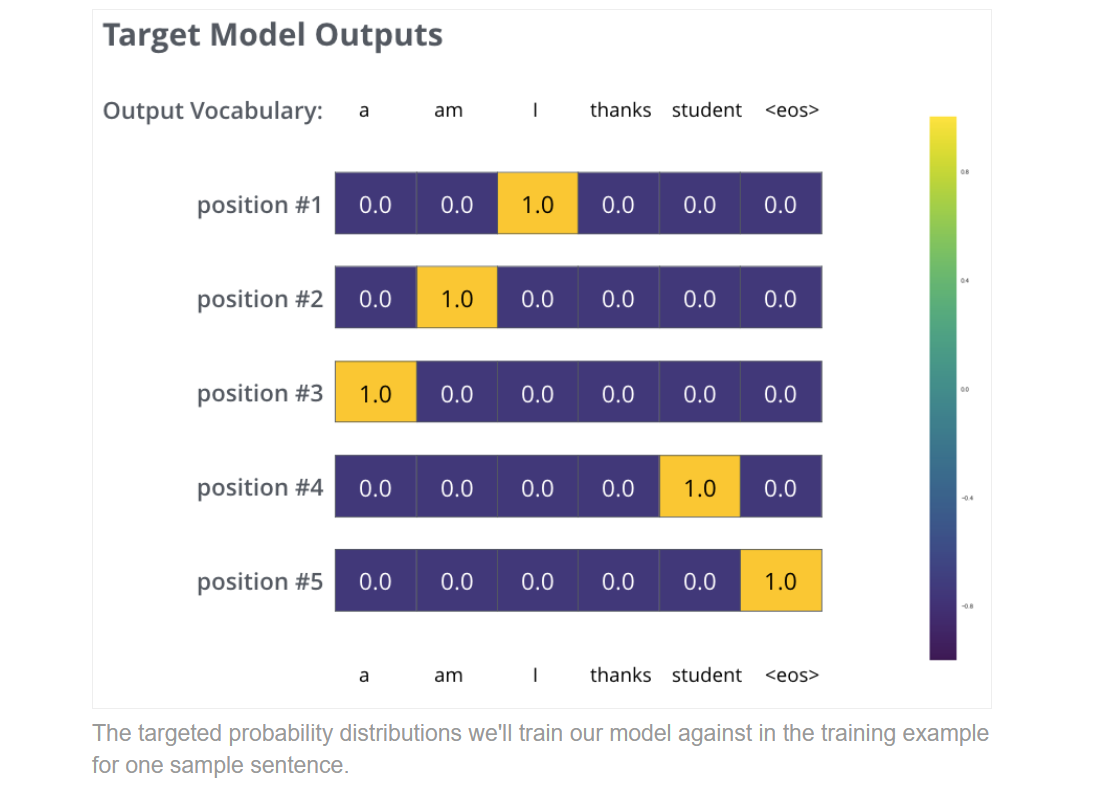
当然经过训练和softmax层，我们期待的模型如下：

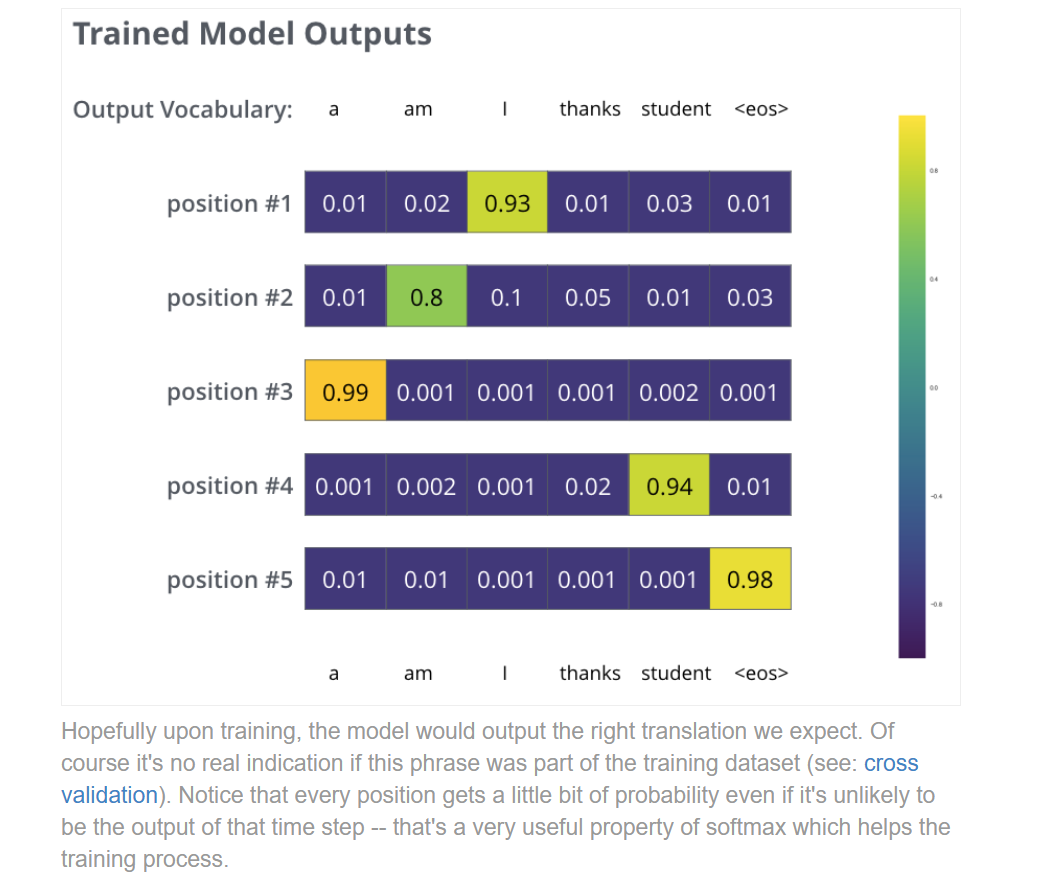
因为模型是每个time step输出一个word的，那么具体选择哪个word作为输出，就有很多思想和方法了。

selecting the word with the highest probability from that probability distribution and throwing away the rest.这是典型的贪心选择greedy decoding。
每次选择top k个，然后分别看其效果（损失值小）进行选择。这种方法是beam search，也很经典。相比较greedy decoding，计算代价要更大复杂度也高了很多，但更能接近全局最优，而贪心容易陷入局部最优的困境。

下面这段很简单直观说明了二者，很精准和易懂。

Now, because the model produces the outputs one at a time, we can assume that the model is selecting the word with the highest probability from that probability distribution and throwing away the rest. That’s one way to do it (called greedy decoding). Another way to do it would be to hold on to, say, the top two words (say, ‘I’ and ‘a’ for example), then in the next step, run the model twice: once assuming the first output position was the word ‘I’, and another time assuming the first output position was the word ‘a’, and whichever version produced less error considering both positions #1 and #2 is kept. We repeat this for positions #2 and #3…etc. This method is called “beam search”, where in our example, beam_size was two (meaning that at all times, two partial hypotheses (unfinished translations) are kept in memory), and top_beams is also two (meaning we’ll return two translations). These are both hyperparameters that you can experiment with.

至此，我们基本完成了transformer的整个模型架构的学习。舒服了。

最后附上standford认为transformer可以更fix的一些点：
1. 注意力机制的pairs计算随着sequence的增长，计算复杂度的计算量是二次方级别的，这一点确实是比RNN更复杂。
2. 关于位置编码positional encoding，有很多更新更好的优化。

整个的transformer理解，确实耗费了很多时间，但捋清楚原理、明确计算过程的那一刻确实是爽爆了。希望我的整理与理解可以帮助更多人深入了解transformer的本质。

当然这篇文章还有很多不足，比如对源码的涉及比较少，这也是后续更新此系列的优化点吧hh。后面也会对面试中涉及transformer很多重要、有趣和我们平时会忽略的问题进行理解和整理。

期待大家的反馈与批评指正~

参考致谢

本文在撰写和整理的整个过程，参考了大量资料，以下参考无先后顺序，致以诚挚的感谢！

0 评论

App 内打开