可能更好的阅读体验

相关链接

题单：https://www.luogu.com.cn/training/79728

文章：https://www.cnblogs.com/streamazure/p/13778319.html

https://oi-wiki.org/graph/bi-graph/

二分图的判定

如果一张无向图，可以将图中的点分成两个集合 $A,B$，使得同一个集合的所有点互不相交，那么它即是一个二分图，$A$ 是集合的左部，$B$ 是集合的右部。

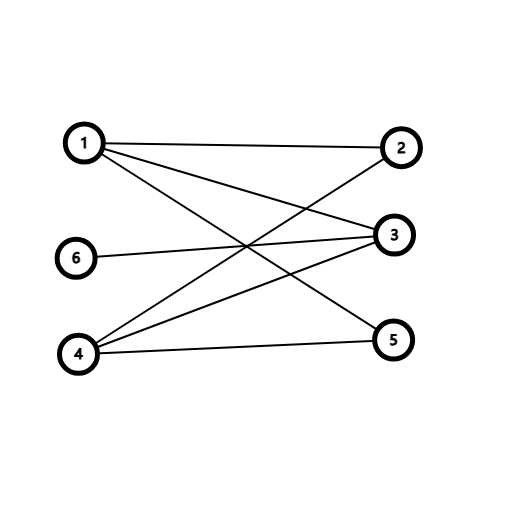
如图即是一个二分图，$A$ 包含了 ${1,4,6}$，$B$ 包含了 $2,3,5$。

二分图的性质有这些：

• 对二分图进行染色，相邻的点不可以染同色，用两个颜色即可覆盖这个图。

• 二分图没有长度为奇数的环，因为每一次都会从一个一个集合到另一个集合。

我们可以运用这些性质来进行判定。每次从一个未染色点出发，如果有颜色而且是同色，那么不是二分图，否则给相邻的点染上反色，并继续向下搜索。

关联题目：P1330 封锁阳光大学

代码

#define maxn 10050
int n,m;
vector<int>G[maxn];
int col[maxn],bel[maxn];
int sum[3][maxn];
bool flg=0;
bool dfs(int now,int c,int nth) {
    col[now]=c; bel[now]=nth;
    for(auto nxt:G[now]) {
        if(col[nxt]==c) return 0; 
        if(!col[nxt]&&!dfs(nxt,3-c,nth)) return 0; 
    }
    return 1;
}
signed main() {
    in2(n,m);
    For(i,1,m) {
        int a,b;
        in2(a,b);
        pb(G[a],b);
        pb(G[b],a);
    }
    int tot=0;
    For(i,1,n)
        if(!col[i]) 
            if(!dfs(i,1,++tot))
                return cout<<"Impossible",0;
    int cnt=0;
    For(i,1,n) sum[col[i]][bel[i]]++;
    For(i,1,tot) cnt+=min(sum[1][i],sum[2][i]);
    cout<<cnt;
}

二分图最大匹配

匹配或是独立边集是一张图中不具有公共端点的边的集合。

左部的点集 $A$ 和右部的点集 $B$，枚举左部的点，尝试向右寻找一个点 $B_i$，使得 $B_i$ 要么暂时没有被其他左部的点选中，要么可以使得改变其他的左部点的匹配方式，使得 $B_i$ 未被选中。

由于最大匹配的边数是确定的，所以我们可以随便选一个起点。

关联题目：P3386 【模板】二分图最大匹配

代码

#define maxn 510
int n,m,e,ans,G[maxn][maxn],to[maxn],u,v;
bool vis[maxn];
bool dfs(int now) {
    For(i,1,m) if(G[now][i]&&!vis[i]) {
        vis[i]=1;
        if(!to[i]||dfs(to[i])) return to[i]=now,1;
    }
    return 0;
}
signed main() {
    in3(n,m,e);
    For(i,1,e) in2(u,v),G[u][v]=1;
    For(i,1,n) m0(vis),ans+=dfs(i);
    cout<<ans;
}