01_差分 difference

差分与前缀和互为逆运算（注: 下标从1开始）

（1）一维差分: （区间修改）

A[1], A[2], … , A[n]（前缀和数组），构造 B[1], B[2], … , B[n]（差分数组）, 
使得 A[i] = B[1] + B[2] + … + B[i]: 
    B[1] = A[1], 
    B[2] = A[2] - A[1], 
    B[3] = A[3] - A[2],
     … ,
    B[n] = A[n] - A[n-1]
说白了就是: ** A 是 B 的前缀和数组 **

 1）初始化: （1）B[0] = 0，B[i] = A[i] - A[i - 1] (i >= 1)
            （2）另一种初始化方式: 
                一开始 A、B 数组都全为 0，可将 B 数组视作 A 数组的差分数组。
                题干中的原数组 A 相当于在区间 [i, i] 上加上 A[i]，
                此时通过 B 数组进行修改操作后，A 数组没有变，但却求出了原数组 A 所对应的差分数组 B 
                void insert(int l, int r, int C) {
                    B[l] += C, B[r + 1] -= C;
                }
                insert(i, i, A[i]);
                例: B[1] = A[1], B[2] = -A[1];
                    B[2] = A[2] - A[1], B[3] = -A[2];
                    B[3] = A[3] - A[2], B[4] = -A[3];
 2）作  用: 通过操作差分数组 B（O(1)）然后遍历计算前缀和（O(n)）实现数组 A 的区间修改
            例：在区间 [l, r] 内，让 A 数组都加上一个 C
                常规算法: O(n * m) -> 遍历加
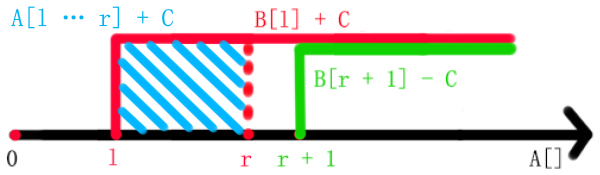
                差分算法: O(n + m) -> 如下图所示: 
                                      B[l] + C;     // A[l ~ n] + C
                                      B[r + 1] - C; // A[r + 1 ~ n] - C，上面多加的 C 被抵消了

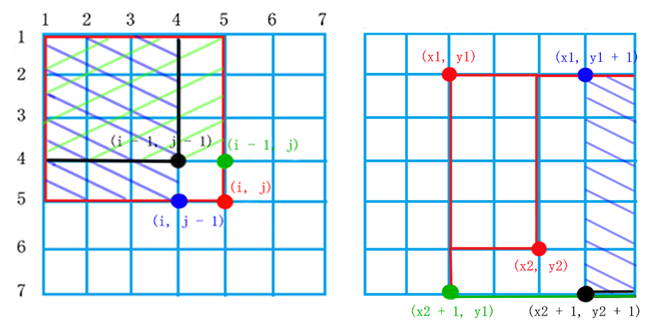
（2）二维差分: （区域修改，如下图所示）

** 二维前缀和是看左上角区域，二维差分是看右下角区域 **

 1）初始化: （1）B[0][0] = 0，B[i][j] = A[i][j] - A[i - 1][j] - A[i][j - 1] + A[i - 1][j - 1];
            （2）另一种初始化: 逻辑同一维差分
                void insert(int x1, int y1, int x2, int y2, int C) {
                    B[x1][y1] += C;
                    B[x1][y2 + 1] -= C;
                    B[x2 + 1][y1] -= C;
                    B[x2 + 1][y2 + 1] += C;
                }
                insert(i, j, i, j, A[i][j]);
 2）作  用: 通过操作差分数组 B（O(1)）然后遍历计算前缀和（O(n * m)）实现数组 A 的区域修改
            例: (x1, y1) -> 区域左上角，(x2, y2) -> 区域右下角，在该区域内，让 A 数组都加上一个 C
            常规算法: O(n * m * q) -> 遍历加
            差分算法: O(n * m + q) -> 如下图所示:
                                      B[x1][y1] += C;
                                      B[x1][y2 + 1] -= C;
                                      B[x2 + 1][y1] -= C;
                                      B[x2 + 1][y2 + 1] += C;

#include <iostream>

using namespace std;

const int N = 100010;
int n, m;
int a[N], b[N];

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);

        /*
        void insert(int l, int r, int c) {
            b[l] += c, b[r + 1] -= c;
        }
        insert(i, i, a[i]);
        */
        b[i] = a[i] - a[i - 1]; // 初始化差分数组
    }

    while (m--) {
        int l, r, c;
        scanf("%d%d%d", &l, &r, &c);
        b[l] += c, b[r + 1] -= c; // 操作差分数组
    }

    for (int i = 1; i <= n; i++) {
        // a[i] = a[i - 1] + b[i]; // 计算前缀和得到结果数组
        // printf("%d ", a[i]);
        b[i] += b[i - 1]; // 计算前缀和得到结果数组
        printf("%d ", b[i]);
    }

    return 0;
}

02_差分矩阵 difference_matrix

#include <iostream>

using namespace std;

const int N = 1010;
int n, m, q;
int a[N][N], b[N][N];

int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            scanf("%d", &a[i][j]);

            /*
            void insert(int x1, int y1, int x2, int y2, int c) {
                b[x1][y1] += c;
                b[x1][y2 + 1] -= c;
                b[x2 + 1][y1] -= c;
                b[x2 + 1][y2 + 1] += c;
            }
            insert(i, j, i, j, a[i][j]);
            */
            b[i][j] = a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1]; // 初始化差分数组
        }
    }

    while (q--) {
        int x1, y1, x2, y2, c;
        scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
        b[x1][y1] += c;
        b[x2 + 1][y1] -= c;
        b[x1][y2 + 1] -= c;
        b[x2 + 1][y2 + 1] += c; // 操作差分数组
    }

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            // a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] 
            //           + b[i][j]; // 计算前缀和得到结果数组
            // printf("%d ", a[i][j]);
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]; // 计算前缀和得到结果数组
            printf("%d ", b[i][j]);
        }
        puts("");
    }

    return 0;
}