01_前缀和 prefix_sum

差分与前缀和互为逆运算（注: 下标从1开始）

（1）一维前缀和（区间和）

S[i] = A[1] + A[2] + … + A[i]

1）初始化: S[0] = 0，S[i] = S[i - 1] + A[i] (i >= 1)
2）作  用: 计算区间和
            例: 区间 [l, r] 的和 (A[l] + … + A[r]): 
                常规算法: O(n) -> 遍历加起来
                前缀和算法: O(1) -> S[r] - S[l - 1]

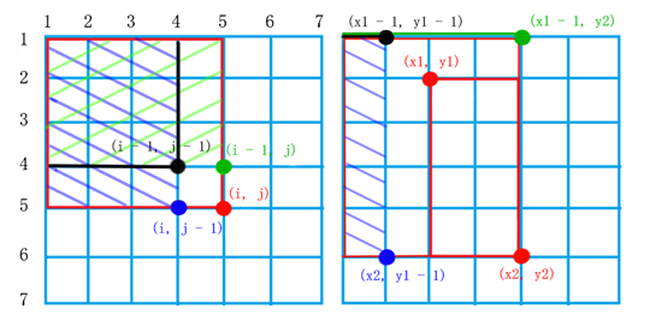
（2）二维前缀和（区域和，如下图所示）

** 二维前缀和是看左上角区域，二维差分是看右下角区域 **

1）初始化: S[0][0] = 0，S[i][j] = S[i-1][j] + S[i][j-1] - S[i-1][j-1] + a[i][j] (i >= 1)
            其中 -S[i-1][j-1]: 多减了一块，加上
2）作  用: 计算区域和
            例: 左上角坐标(x1, y1)和右下角坐标(x2, y2)围成的区域和: 
                常规算法: O(n^2) -> 遍历加起来
                前缀和算法: O(1) -> S[x2][y2] - S[x2][y1-1] - S[x1-1][y2] + S[x1-1][y1-1]

#include <iostream>

using namespace std;

const int N = 100010;
int n, m;
int a[N], s[N];

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        s[i] = s[i - 1] + a[i]; // 初始化前缀和数组
    }

    while (m--) {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", s[r] - s[l - 1]); // 计算区间和
    }

    return 0;
}

02_子矩阵的和 submatrice_sum

#include <iostream>

using namespace std;

const int N = 1010;
int n, m, q;
int a[N][N], s[N][N];

int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            scanf("%d", &a[i][j]);
            // 初始化前缀和数组
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
        }
    }

    while (q--) {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        // 计算区域和
        printf("%d\n", s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]);
    }

    return 0;
}