1.矩阵左乘
向量都是列向量,即
[3]
[6]
[3]
[4]

m4x4 * v4 结果是一个列向量
即一个 4x4矩阵乘以一个 4x1 矩阵，结果时 4x1矩阵
即一个列向量

如果是多个矩阵的复合变换。即顶点需要乘多个矩阵进行变换。
那么为了保证最终的结果也是顶点。所以顶点要放在最后。
即顶点左乘一个矩阵，才能保证变换后还是顶点。
因为矩阵乘法不满足交换律，即不是阿贝尔群。但有结合律

m1 * m2 * m3 * v
-> m1 * m2 * (m3 * v)
-> m1 * (m2 * v2)
-> m1 * v3
-> v4

2.shader代码
具体矩阵相乘，参看代码注释
下面的变换相当于

总的: MVP * mat * vertex
因为vertex 是模型坐标，而旋转操作是对模型坐标进行操作
所以 MVP要放在最后乘
顺序是不能改变的,非阿贝尔群嘛。
但是因为结合律，可以先算 MVP * mat

即:
MVP * mat * vertex
-> (MVP * mat) * vertex
-> mat2 * vertex
-> vertex2

因为是对所有顶点都旋转，那么效果就相当于对整个物体进行旋转了

Shader "Custom/twistPlane"
{
    Properties
    {

    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 100

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
            };

            v2f vert (appdata v)
            {
                //模型坐标
                float angle = _Time * 20;
                float4x4 mat = float4x4(
                    cos(angle),0,sin(angle),0,
                    0,1,0,0,
                    -sin(angle),0,cos(angle),0,
                    0,0,0,1
                );
                float4x4 mvp = float4x4(UNITY_MATRIX_MVP);
                //注意这个地方的相乘顺序
                //多个变换的时候，要左乘。因为最后返回的是一个矩阵，所以向量要放最后
                //即 m1*m2*vec,这样才能保证乘出来的结果是一个4x1的向量
                mat = mul(mvp,mat);
                v2f o;
                o.vertex = mul(mat,v.vertex);
                o.uv = v.uv;
                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
                return fixed4(1,1,0,1);
            }
            ENDCG
        }
    }
}

3.效果

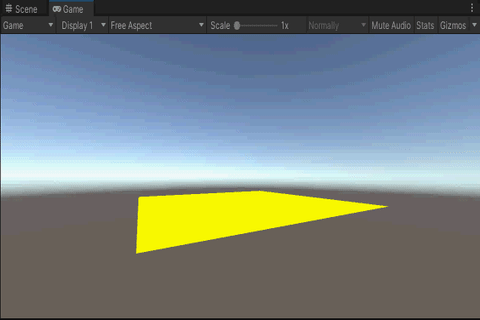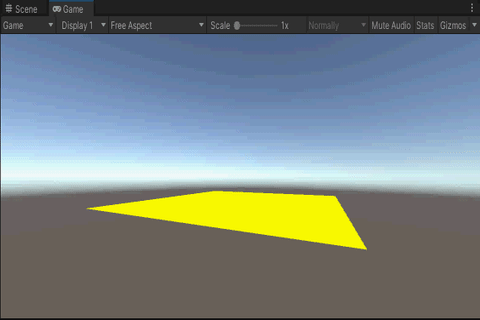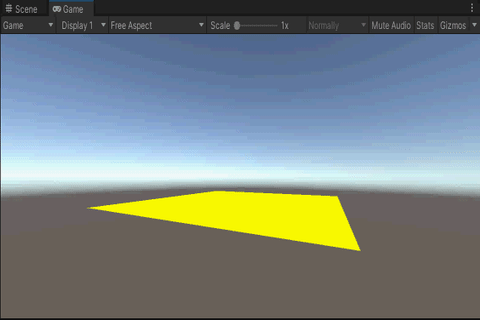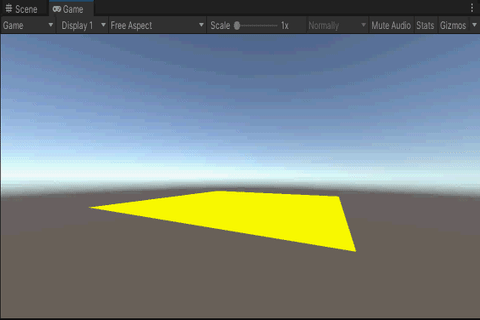
4.总结
特别要注意矩阵的相乘顺序，要不然最终结果可能大相径庭。

另外附上shaderlab中的矩阵定义

float4x4 m = float4x4(1.1, 1.2, 1.3, 1.4,
                                    2.1, 2.2, 2.3, 2.4,
                                    3.1, 3.2, 3.3, 3.4,
                                    4.1, 4.2, 4.3, 4.4);
float3x3 n = float3x3(m);  
float4x4 m = float4x4(1.1, 1.2, 1.3, 1.4,
                                    2.1, 2.2, 2.3, 2.4,
                                    3.1, 3.2, 3.3, 3.4,
                                    4.1, 4.2, 4.3, 4.4);
float3x3 n = float3x3(m);  
//相当于float3x3(1.1, 1.2, 1.3, 2.1, 2.2, 2.3, 3.1, 3.2, 3.3)

向量定义1

float2 a = float2(1.0, 2.0);
float3 b = float3(-1.0, 0.0, 0.0);
float4 c = float4(0.0, 0.0, 0.0, 1.0);

向量定义2

float4 a = float4(0.0);
//相当于float4(0.0, 0.0, 0.0, 0.0)