名言:自己写的总结, 从来只有自己看, 永远不会有其他人看… 🤡

这篇总结和昨天的总结合并了, 昨天的已删除

强连通分量 SCC

1. 强连通:若有向图中点x能有路径到达y, y也有路径到达x, 称x和y是强连通的(无向图中的是双连通, 一般简称连通);

2. 强连通图: 一张有向图, 图中任意两点都是强连通的;

3. 强连通分量(Component): 有向图的极大连通子图(意思就是一个有向图不能再大了, 再大就不是连通子图了);

例如:

Tajan算法 $O(N+M)$

1. 维护dfn[i]表示点i的dfs序(更新在递归之前);

2. 维护low[i]表示点i能到达的最小时间戳(low[i]一定是在回溯之后更新);

3. 用栈存储首次访问的点的编号;

4. 当出现关键点low[i] == dfn[i], 是栈顶一直到i的点都属于同一个SCC;

5. 栈是拿来判断那些点在一个强连通分量, 越晚出现的点越小

模板题目 B3609 [图论与代数结构 701] 强连通分量

代码实现:

#include <bits/stdc++.h>
using namespace std;

const int N = 1e4 + 10, M = 1e5 + 10;
int h[N], e[M], ne[M], idx;
bool st[N];
int dfn[N], low[N], timestamp;
int scc[N], cnt;
stack<int> s;
vector<int> g[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void tarjan(int u) // 当前访问到的节点
{
    s.push(u); // 把没有确定SCC的点都放入栈中

    st[u] = true; // 表示u此时在栈中

    dfn[u] = low[u] = ++timestamp; // 初始化u的最小时间戳

    for (int i = h[u]; ~i; i = ne[i]) // u指向的点
    {
        int j = e[i];

        if (!dfn[j]) // 未访问
        {
            tarjan(j);

            low[u] = min(low[u], low[j]);
        }
        else if (st[j]) // 访问过, 在栈里, u和j都属于同一个SCC
            low[u] = min(low[u], low[j]); // 在强连通分量里, 这里的low[j]和dfn[j]是没区别的, 也可以写 low[u] = min(low[u], dfn[j]);
    }

    if (low[u] == dfn[u]) // 关键点
    {
        cnt++; // 统计SCC的个数

        while (s.top() != u) // 弹出u上面的节点
        {
            int t = s.top();
            s.pop();

            g[cnt].push_back(t); // 将t存入第cnt个数组

            st[t] = false;
            scc[t] = cnt; // 点u也属于第cnt个SCC
        }

        s.pop(); // 点u

        st[u] = false;
        scc[u] = cnt; // 点u属于第cnt个SCC
        g[cnt].push_back(u);
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0); 
    cout.tie(0);

    int n, m;
    cin >> n >> m;

    memset(h, -1, sizeof h);

    int a, b;
    while (m--)
    {
        cin >> a >> b;

        add(a, b); // 有向边
    }

    for (int i = 1; i <= n; i++) // 图可能不连通
        if (!dfn[i]) // 点i还没有访问
            tarjan(i);

    cout << cnt << '\n'; // SCC的数量

    for (int i = 1; i <= n; i++)
        if (dfn[i]) // dfn[i] != 0 未输出
        {
            sort(g[scc[i]].begin(), g[scc[i]].end()); // 排序

            for (auto j : g[scc[i]])
            {
                cout << j << ' ';
                dfn[j] = 0; //dfn清零, 防止重复输出
            }

            cout << '\n';
        }


    return 0;
}

例题:

P2169 正则表达式

1. 跑强连通分量, 题目说两个互相连接的点的权值为0, 我们可以直接把这个连通块缩减成一个点;

2. 缩点后, 将SCC建新图;

3. 新图跑dijkstra

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;

const int N = 2e5 + 10, M = 2e6 + 10;
int a[N], b[N], c[N];
int h[N], e[M], w[M], ne[M], idx;
bool st[N];
int dfn[N], low[N], timestamp;
int scc[N], cnt;
int d[N];
stack<int> s;

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void tarjan(int u)
{
    s.push(u);

    st[u] = true;

    dfn[u] = low[u] = ++timestamp;

    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];

        if (!dfn[j])
        {
            tarjan(j);

            low[u] = min(low[u], low[j]);
        }
        else if (st[j])
            low[u] = min(low[u], low[j]);
    }

    if (low[u] == dfn[u])
    {
        cnt++;

        while (s.top() != u)
        {
            int t = s.top();
            s.pop();

            st[t] = false;
            scc[t] = cnt;
        }

        s.pop();

        st[u] = false;
        scc[u] = cnt;
    }
}

void dijkstra(int s)
{
    priority_queue<PII, vector<PII>, greater<PII>> heap;

    memset(d, 0x3f, sizeof d);

    d[s] = 0;

    heap.push({0, s});

    while (heap.size())
    {
        PII t = heap.top();
        heap.pop();

        int dist = t.first, v = t.second;

        if (!st[v])
        {
            for (int i = h[v]; ~i; i = ne[i])
            {
                int j = e[i];

                if (d[j] > dist + w[i])
                {
                    d[j] = dist + w[i];
                    heap.push({d[j], j});
                }
            }

            st[v] = true;
        }
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0); 
    cout.tie(0);

    int n, m;
    cin >> n >> m;

    memset(h, -1, sizeof h);

    for (int i = 0; i < m; i++)
    {
        cin >> a[i] >> b[i] >> c[i];

        add(a[i], b[i], c[i]);
    }

    for (int i = 1; i <= n; i++)
        if (!dfn[i]) tarjan(i);

    idx = 0;
    memset(st, 0, sizeof st);
    memset(h, -1, sizeof h);

    for (int i = 0; i < m; i++)
        if (scc[a[i]] != scc[b[i]]) add(scc[a[i]], scc[b[i]], c[i]);

    dijkstra(scc[1]);

    cout << d[scc[n]];


    return 0;
}

P3387 【模板】缩点

先跑tarjan, 再跑拓扑, 板子题

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6;
int a[N], b[N];
int h[N], e[N], w[N], ne[N], idx;
bool st[N];
int dfn[N], low[N], timestamp;
int scc[N], cnt;
int d[N], f[N], s[N];
stack<int> S;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void tarjan(int u)
{
    S.push(u);

    st[u] = true;

    dfn[u] = low[u] = ++timestamp;

    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];

        if (!dfn[j])
        {
            tarjan(j);

            low[u] = min(low[u], low[j]);
        }
        else if (st[j])
            low[u] = min(low[u], low[j]);
    }

    if (low[u] == dfn[u])
    {
        cnt++;

        while (S.top() != u)
        {
            int t = S.top();
            S.pop();

            st[t] = false;
            scc[t] = cnt;
            s[cnt] += w[t];
        }

        S.pop();

        st[u] = false;
        scc[u] = cnt;
        s[cnt] += w[u];
    }
}

void topsort()
{
    queue<int> q;

    for (int i = 1; i <= cnt; i++)
        if (!d[i])
        {
            f[i] = s[i];
            q.push(i);
        }

    while (q.size())
    {
        int t = q.front();
        q.pop();

        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];

            f[j] = max(f[j], f[t] + s[j]);

            if (--d[j] == 0) q.push(j);
        }
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0); 
    cout.tie(0);

    int n, m;
    cin >> n >> m;

    memset(h, -1, sizeof h);

    for (int i = 1; i <= n; i++) cin >> w[i];

    for (int i = 0; i < m; i++)
    {
        cin >> a[i] >> b[i];

        add(a[i], b[i]);
    }

    for (int i = 1; i <= n; i++)
        if (!dfn[i]) tarjan(i);

    idx = 0;
    memset(h, -1, sizeof h);

    for (int i = 0; i < m; i++)
        if (scc[a[i]] != scc[b[i]])
        {
            add(scc[a[i]], scc[b[i]]);
            d[scc[b[i]]]++;
        }

    topsort();

    int res = 0;
    for (int i = 1; i <= cnt; i++) res = max(res, f[i]);

    cout << res;


    return 0;
}

CF949C Data Center Maintenance

好题+1👌

题意: n个数据中心, m份资料, 每份资料存在两个不同的数据中心, 且两个数据中心的维护时间不一样, 现在求最少推迟几个数据中心的维护时间, 使得m份资料仍然保证份两个数据中心时间不一样.

分析:

1. 当1个数据中心x推迟一小时维护, 可能会引起连锁反应;

2. 将数据中心当作点, 若x推迟导致y必须也推迟, x向y连有向边;

3. 若(t[x]+1)%h == t[y]%h, add(a, b), 若(t[y] + 1) % h == t[x] % h, 建反边;

4. 若图无环随便选一个出度为0的点, 答案就是1;

5. 若图有环, 缩点, 并维护强连通中原始点的个数num[i];

6. 答案是新图中出度为0的强连通中num的最小值

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;

const int N = 2e5 + 10;
int c[N];
int h[N], e[N], ne[N], idx;
bool st[N];
int dfn[N], low[N], timestamp;
int scc[N], cnt;
int S[N], d[N];
stack<int> s;
vector<PII> g;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void tarjan(int u)
{
    s.push(u);

    st[u] = true;

    dfn[u] = low[u] = ++timestamp;

    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];

        if (!dfn[j])
        {
            tarjan(j);

            low[u] = min(low[u], low[j]);
        }
        else if (st[j])
            low[u] = min(low[u], low[j]);
    }

    if (low[u] == dfn[u])
    {
        cnt++;

        while (s.top() != u)
        {
            int t = s.top();
            s.pop();

            S[cnt]++;
            st[t] = false;
            scc[t] = cnt;
        }

        s.pop();

        st[u] = false;
        scc[u] = cnt;
        S[cnt]++;
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0); 
    cout.tie(0);

    int n, m, H;
    cin >> n >> m >> H;

    for (int i = 1; i <= n; i++) cin >> c[i];

    memset(h, -1, sizeof h);

    int a, b;
    for (int i = 1; i <= m; i++)
    {
        cin >> a >> b;

        if ((c[a] + 1) % H == c[b]) add(a, b), g.push_back({a, b});
        if ((c[b] + 1) % H == c[a]) add(b, a), g.push_back({b, a});
    }

    for (int i = 1; i <= n; i++)
        if (!dfn[i]) tarjan(i);

    for (auto i : g)
        if (scc[i.first] != scc[i.second]) d[scc[i.first]]++;

    S[0] = 1e9;

    int p = 0;
    for (int i = 1; i <= cnt; i++)
        if (!d[i] && S[p] > S[i]) p = i;

    cout << S[p] << '\n';

    for (int i = 1; i <= n; i++)
        if (scc[i] == p) cout << i << ' ';


    return 0;
}

P1262 间谍网络

时间复杂度 $O(N+R)$

题意: 有n个点, r条边, p个点有点权, 求是否能够控制若干有点权的点, 从而控制所有的点, 以及最少花费;

分析:

1. 若图是有向无环图, 那么贪心的选择入度为0的点最优;

2. 若存在入度为0的点x, 且x没有点权, 无解;

3. 若有解, 入度为0的所有点的权值之和即为答案 ;

4. 若图中存在环, 那么只需要用环上点权最小的值代表整个”大点”;

5. 细节上, 没有点权可以设为极大值1e9;

6. 第1个权值为1e9开始tarjan的点, 就是无法控制的最小编号的点;

#include <bits/stdc++.h>
using namespace std;

const int N = 8010, M = 2e4 + 10, INF = 0x3f3f3f3f;
int h[N], e[M], ne[M], idx;
int dfn[M], low[M], s[N];
int len[M], f[M], g[N];
bool st[N];
int p[N];
int tt, cnt, timestamp;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void tarjan(int u)
{
    dfn[u] = low[u] = ++timestamp;

    st[u] = true;
    s[++tt] = u;

    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];

        if (!dfn[j])
        {
            tarjan(j);
            low[u] = min(low[u], low[j]);
        }
        else if (st[j])
            low[u] = min(low[u], low[j]);
    }

    if (dfn[u] == low[u])
    {
        cnt++;

        while (s[tt + 1] != u)
        {
            int t = s[tt--];

            g[t] = cnt;
            st[t] = false;
            len[cnt]++;
            f[cnt] = min(f[cnt], p[t]);
        }
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    int n;
    cin >> n;

    memset(p, 0x3f, sizeof p);
    memset(f, 0x3f, sizeof f);

    int m;
    cin >> m;

    int a, b;
    while (m--)
    {
        cin >> a >> b;

        p[a] = b;
    }

    cin >> m;

    memset(h, -1, sizeof h);

    while (m--)
    {
        cin >> a >> b;

        add(a, b);
    }

    for (int i = 1; i <= n; i++)
        if (!dfn[i] && p[i] != INF) tarjan(i);

    for (int i = 1; i <= n; i++)
        if (!dfn[i])
        {
            cout << "NO\n";
            cout << i << '\n';
            return 0;
        }

    memset(st, 0, sizeof st);

    for (int i = 1; i <= n; i++)
        for (int j = h[i]; ~j; j = ne[j])
            if (g[i] != g[e[j]]) st[g[e[j]]] = true;

    cout << "YES\n";

    int res = 0;
    for (int i = 1; i <= cnt; i++)
        if (!st[i]) res += f[i];

    cout << res;


    return 0;
}

P1407 [国家集训队] 稳定婚姻

分析:

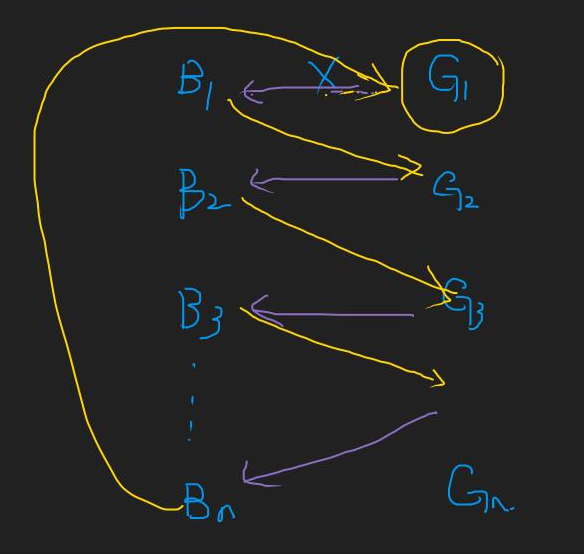
1. 在给定的n个关系中, B向G建边;

2. 在给定的m组情侣关系中, G向B建边;

3. 若关系不稳定, 则一定有”环”;

4. 若scc[B[i]]==scc[g[i]], 则第i组关系不稳定. 否则, 稳定

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10, M = 4e5 + 10;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int scc[N], cnt;
string g[N];
bool st[M];
stack<int> s;
map<string, int> w;

void add(int a, int b) 
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void tarjan(int u)
{
    s.push(u);

    st[u] = true;

    dfn[u] = low[u] = ++timestamp;

    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];

        if (!dfn[j])
        {
            tarjan(j);

            low[u] = min(low[u], low[j]);
        }
        else if (st[j])
            low[u] = min(low[u], low[j]);
    }

    if (low[u] == dfn[u])
    {
        cnt++;

        while (s.top() != u)
        {
            int t = s.top();
            s.pop();

            st[t] = false;
            scc[t] = cnt;
        }

        s.pop();

        st[u] = false;
        scc[u] = cnt;
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    int n;
    cin >> n;

    memset(h, -1, sizeof h);

    string a, b;
    int cnt = 0;
    for (int i = 0; i < n; i++)
    {
        cin >> a >> b;

        g[++cnt] = a, w[a] = cnt;
        g[++cnt] = b, w[b] = cnt;

        add(cnt - 1, cnt);
    } 

    int m;
    cin >> m;

    while (m--)
    {
        cin >> a >> b;

        add(w[b], w[a]);
    }

    for (int i = 1; i <= cnt; i++)
        if (!dfn[i]) tarjan(i);

    for (int i = 1; i <= 2 * n; i += 2)
        if (scc[i] != scc[i + 1]) cout << "Safe\n";
        else cout << "Unsafe\n";


    return 0;
}

P3275 [SCOI2011] 糖果

1. 若A<B, 可以理解为A的糖果数至少比B少1颗, A向B连边, 权值为1;

2. 若A>B, B向A连边, 权值为1;

3. 若A<=B, 从贪心的角度, 取等于最好, A向B连边, 权值为 0;

4. 若A>=B, B向A连边, 权值为0

5. 若A==B, A向B, B向A连边, 权值均为0;

6. 若该图是有向无环图, 定义f[i]表示点i最少发的糖果数;

7. 转移: cur->nxt, f[nxt] = max(f[nxt], f[cur] + w);

8. 答案: ans += f[i];

9. 初始化: f[i] = 1;

10. 若有环, 则先缩点, 若环上有边权为1, 则无解

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;

typedef long long ll;

const int N = 2e5;
int dfn[N], low[N], timestamp;
bool st[N];
int scc[N], cnt;
vector<PII> g1[N], g2[N];
stack<int> s;
int d[N];
ll f[N], num[N];

void tarjan(int u)
{
    s.push(u);

    st[u] = true;

    dfn[u] = low[u] = ++timestamp;

    for (auto i : g1[u])
    {
        int j = i.first;

        if (!dfn[j])
        {
            tarjan(j);

            low[u] = min(low[u], low[j]);
        }
        else if (st[j])
            low[u] = min(low[u], low[j]);
    }

    if (low[u] == dfn[u])
    {
        cnt++;

        while (s.top() != u)
        {
            int t = s.top();
            s.pop();

            num[cnt]++;
            st[t] = false;
            scc[t] = cnt;
        }

        s.pop();

        num[cnt]++;
        st[u] = false;
        scc[u] = cnt;
    }
}

void topsort()
{
    queue<int> q;
    for (int i = 1; i <= cnt; i++)
        if (!d[i])
        {
            q.push(i);
            f[i] = 1;
        }

    while (q.size())
    {
        int t = q.front();
        q.pop();

        for (auto i : g2[t])
        {
            int j = i.first, w = i.second;

            f[j] = max(f[j], f[t] + w);

            if (--d[j] == 0) q.push(j);
        }
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0); 
    cout.tie(0);

    int n, k;
    cin >> n >> k;

    int op, a, b;
    while (k--)
    {
        cin >> op >> a >> b;

        if (op == 1)
        {
            g1[a].push_back({b, 0});
            g1[b].push_back({a, 0});
        }
        else if (op == 2) g1[a].push_back({b, 1});
        else if (op == 3) g1[b].push_back({a, 0});
        else if (op == 4) g1[b].push_back({a, 1});
        else g1[a].push_back({b, 0});
    }

    for (int i = 1; i <= n; i++)
        if (!dfn[i]) tarjan(i);

    for (int i = 1; i <= n; i++)
        for (auto j : g1[i])
        {
            int k = j.first, w = j.second;

            if (scc[i] == scc[k])
            {
                if (w)
                {
                    cout << -1;
                    return 0;
                }
            }
            else
            {
                g2[scc[i]].push_back({scc[k], w});
                d[scc[k]]++;
            }
        }

    topsort();

    ll res = 0;
    for (int i = 1; i <= cnt; i++)
        res += f[i] * num[i];

    cout << res;


    return 0;
}