拓扑排序:

对于n个点的 有向无环图 , 整理出一个点的顺序, 使得所有边的出点都在入点之前

得到的顺序称为拓扑序(不一定唯一)

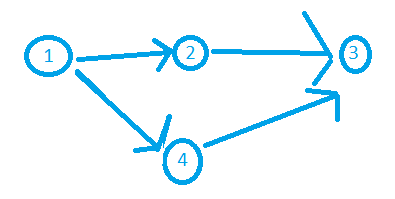
拓扑排序的实现

1. 统计所有点的入度in[x];

2. 将入度为0的点入队或入栈

3. 循环从对头取出一个点x， 将x的邻接点y的入度减1, in[y]–

4. 若in[y]==0, 将y入队或者入栈

5. 重复执行3~4, 知道队列为空

板子题 B3644 【模板】拓扑排序 / 家谱树

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10;
int e[N], ne[N], h[N], idx; 
int q[N], d[N];
int n;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void topsort()
{
    int hh = 0, tt = -1;

    for (int i = 1; i <= n; i++)
            if (!d[i]) q[++tt] = i;

    while (hh <= tt)
    {
        int t = q[hh++];

        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];

            if (--d[j] == 0) q[++tt] = j;
        }
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n;

    memset(h, -1, sizeof h);

    int x;
    for (int i = 1; i <= n; i++)
        while (cin >> x, x) add(i, x), d[x]++;

    topsort();

    for (int i = 0; i < n; i++) cout << q[i] << ' ';


    return 0;
}

拓扑排序的应用

1.判环, 只能判断是否有环以及点是否在环里, 但不能确定在哪个环

2. 提供递推的顺序, 结合动态规划

状态:dp[i]表示以点i结尾的???的最大值,最小值, 方案数

答案: dp[i]或出度为0的点dp

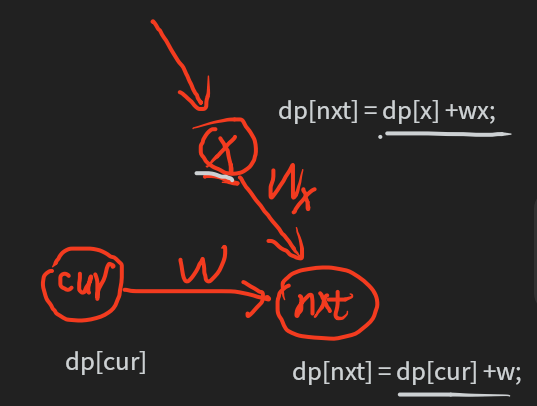
转移: 扩散性转移, 对于cur->nxt

    dp[nxt] = max(dp[nxt], dp[cur] + w);

初始状态:

要么in[i]==0时初始化

要么dp[i]均要初始化

P6145 [USACO20FEB] Timeline G

1.状态: dp[i]表示第i个点的最早挤奶时间

2.答案: dp[i];

3.转移: cur->next

    dp[nxt] = max(dp[nxt], dp[cur] + w); // 注意是max不是min

4. 初始状态：dp[i] = s[i];

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10;
int h[N], e[N], w[N], ne[N], idx;
int f[N];
int d[N];
int n, m, k;

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void topsort()
{
    queue<int> q;

    for (int i = 1; i <= n; i++)
        if (!d[i]) q.push(i);

    while (q.size())
    {
        int t = q.front();
        q.pop();

        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i], k = w[i];

            f[j] = max(f[j], f[t] + k);

            if (--d[j] == 0) q.push(j);
        }
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> n >> m >> k;

    for (int i = 1; i <= n; i++) cin >> f[i];

    memset(h, -1, sizeof h);

    int a, b, c;
    while (k--)
    {
        cin >> a >> b >> c;

        add(a, b, c);
        d[b]++;
    }

    topsort();

    for (int i = 1; i <= n; i++) cout << f[i] << '\n';


    return 0;
}

P4017 最大食物链计数

题意:求入度为0的点到出度为0的点的路径数

状态: dp[i]表示从入度为0的点走到点i的路径数

答案: if(out[i] == 0) res += dp[i];

转移: dp[nxt] += dp[cur];

初始化: if (in[i] == 0) dp[i] = 1;

#include <bits/stdc++.h>
using namespace std;

const int N = 5010, M = 5e5 + 10, mod = 80112002;
int e[M], ne[M], h[N], idx;
int in[N], out[N];
int f[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    int n, m;
    cin >> n >> m;

    memset(h, -1, sizeof h);

    int a, b;
    while (m--)
    {
        cin >> a >> b;

        add(a, b);
        in[b]++, out[a]++;
    }

    queue<int> q;
    for (int i = 1; i <= n; i++) 
        if (!in[i]) q.push(i), f[i] = 1;

    while (q.size())
    {
        int t = q.front();
        q.pop();

        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];

            f[j] = (f[j] + f[t]) % mod;

            if (--in[j] == 0) q.push(j);
        }
    }

    int res = 0;
    for (int i = 1; i <= n; i++)
        if (!out[i]) res = (res + f[i]) % mod;

    cout << res;


    return 0;
}

P2883 [USACO07MAR] Cow Traffic S

题意:给定n个点m条边的有向无环图, 求所有入度为0到出度为0的路径中, 被经过最多边的经过次数.

1. 此题转移和上一题转移相同;

2. 维护dp1[i]表示从入度为0的点到达点i的方案数;

3. 维护dp2[i]表示从点i到出度为0的点的方案数, 建反图后dp2[i]就是dp1[i];

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;

const int N = 5e4 + 10;
int h1[N], e1[N], ne1[N], idx1;
int h2[N], e2[N], ne2[N], idx2;
PII g[N];
int d1[N], d2[N];
int f1[N], f2[N];

void add1(int a, int b)
{
    e1[idx1] = b, ne1[idx1] = h1[a], h1[a] = idx1++; 
}

void add2(int a, int b)
{
    e2[idx2] = b, ne2[idx2] = h2[a], h2[a] = idx2++;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    int n, m;
    cin >> n >> m;

    memset(h1, -1, sizeof h1);
    memset(h2, -1, sizeof h2);

    int a, b;
    for (int i = 0; i < m; i++)
    {
        cin >> a >> b;

        g[i] = {a, b};

        add1(a, b);
        add2(b, a);
        d1[b]++, d2[a]++;
    }

    queue<int> q;

    for (int i = 1; i <= n; i++)
        if (!d1[i]) q.push(i), f1[i] = 1;

    while (q.size())
    {
        int t = q.front();
        q.pop();

        for (int i = h1[t]; ~i; i = ne1[i])
        {
            int j = e1[i];

            f1[j] += f1[t];

            if (--d1[j] == 0) q.push(j);
        }
    }

    q.push(n);
    f2[n] = 1;

    while (q.size())
    {
        int t = q.front();
        q.pop();

        for (int i = h2[t]; ~i; i = ne2[i])
        {
            int j = e2[i];

            f2[j] += f2[t];

            if (--d2[j] == 0) q.push(j);
        }
    }

    int res = 0;
    for (int i = 0; i < m; i++)
        res = max(res, f1[g[i].first] * f2[g[i].second]);

    cout << res;


    return 0;
}