每日一题+1
UVA1316 Supermarket
贪心解法
时间复杂度 $O(N • D)$
1. 按照价格从大到小排序;
2. 贵的物品不一定第一时间卖掉;
3. 早的时间比晚的时间更宝贵;
4. 对于枚举的第i个物品, 尝试第d[i]天卖掉;
5. 若第d[i]天已经卖过物品尝试在d[i]-1天卖掉, 倒序循环找到第1个能卖的时间, 若枚举到0, 说明第i个物品无法卖出
前面的算法虽然能AC但是很慢, 我们可以考虑并查集优化
并查集优化
时间复杂度 $O(N • logN)$
先将商品按照利润排序, 然后贪心的先将利润大的商品卖出.
因此我们需要判断对于当前这个商品来说, 过期日期之前是否还有空余天数来将这个商品卖出.
因此可以用并查集来维护数组中的每一个位置.
终极代码
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e6 + 10;
PII g[N];
int p[N];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
bool cmp(PII a, PII b)
{
return a.first > b.first;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
while (cin >> n)
{
int m = 0;
for (int i = 0; i < n; i++)
{
cin >> g[i].first >> g[i].second;
m = max(m, g[i].second);
}
sort(g, g + n, cmp);
for (int i = 1; i <= m; i++) p[i] = i;
int res = 0;
for (int i = 0; i < n; i++)
{
int P = find(g[i].second);
if (P > 0)
{
res += g[i].first;
p[P] = P - 1;
}
}
cout << res << '\n';
}
return 0;
}
正片开始
种类并查集
处理图论模型中,边的种类多于一种的情形
例题
P1892 [BOI2003] 团伙
1. 把人看作点, 把关系看作边;
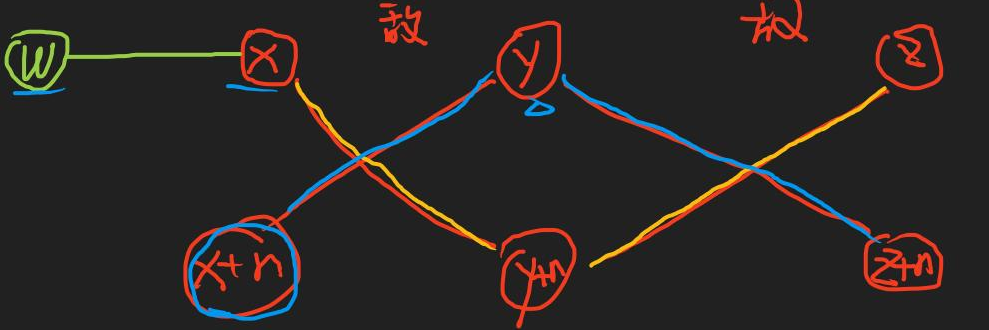
2. 关系分为两类: 朋友与敌人,意味这边应该也有两类;
3. 把一个人拆成x和x+n两个点, 其中x只和朋友连边, x+n只和敌人连边;
4. 若两个点时朋友, 合并(x,y), 否则 合并(x,y+n), 合并(y,x+n);
5. 统计p[i] == i的数量, 要排除虚拟点作为根节点的情况;
6. 合并(x,y)时,要确保编号在n以内的做父节点;
#include <bits/stdc++.h>
using namespace std;
const int N = 2010;
int p[N];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
void Union(int a, int b)
{
a = find(a), b = find(b);
if (a != b) p[b] = a;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n, m;
cin >> n >> m;
for (int i = 1; i <= 2 * n; i++) p[i] = i;
char opt;
int a, b;
while (m--)
{
cin >> opt >> a >> b;
if (opt == 'E')
{
Union(a, b + n);
Union(b, a + n);
}
else Union(a, b);
}
int cnt = 0;
for (int i = 1; i <= n; i++)
if (p[i] == i) cnt++;
cout << cnt;
return 0;
}
CF1594D The Number of Imposters
1. 当i说j是诚实的人, 那么i和j同类;
2. 当i说j是说谎的人, 那么i和j异类;
3. 考虑拆点, 用x和x+n表示x可能的两种类型, 但类型位置;
4. 处理完所有的关系后, x和x+n一定分属2个连通块, 此时取较大的连通块定位“诚实”;
5. 并查集维护s[i]表示以i为根的集合的点数, 那么p[a] = b, s[b] += s[a];
6. 当a与b是同类 合并(x, y), 合并(x + n, y + n);
7. 当a与b是异类 合并(x, y + n), 合并(y, x + n);
#include <bits/stdc++.h>
using namespace std;
const int N = 4e5 + 10;
int p[N], s[N];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int Union(int a, int b)
{
a = find(a), b = find(b);
if (a != b)
{
s[a] += s[b];
s[b] = 0;
p[b] = a;
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
int n, m;
while (t--)
{
cin >> n >> m;
for (int i = 1; i <= 2 * n; i++) p[i] = i, s[i] = i <= n;
int a, b;
string opt;
while (m--)
{
cin >> a >> b >> opt;
if (opt == "imposter")
Union(a, b + n), Union(b, a + n);
else
Union(a, b), Union(a + n, b + n);
}
int res = 0;
for (int i = 1; i <= n; i++)
{
if (find(i) == find(i + n))
{
res = -1;
break;
}
res += max(s[find(i)], s[find(i + n)]);
s[find(i)] = s[find(i + n)] = 0;
}
cout << res << '\n';
}
return 0;
}
P2024 [NOI2001] 食物链
1. 考虑拆点成3分, x, x + n, x + 2n分别代表动物x可能的3种类型;
2. 当x和y是同类, 合并(x, y), 合并(x+n, y+n), 合并(x+2n, y+2n);
3. 当x吃y 合并(x, y+n), 合并(x+n, y+2n), 合并(x+2n, y);
4. 当说x和y是同类, 假话有两种情况 find(x) == find(y+n)或find(y) == find(x+n)
#include <bits/stdc++.h>
using namespace std;
const int N = 1.5e5 + 10;
int p[N];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
void Union(int x, int y)
{
x = find(x), y = find(y);
if (x != y) p[y] = x;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n, m;
cin >> n >> m;
for (int i = 1; i <= 3 * n; i++) p[i] = i;
int cnt = 0;
int opt, x, y;
while (m--)
{
cin >> opt >> x >> y;
if (x > n || y > n) cnt++;
else if (opt == 1)
{
if (find(x) == find(y + n) || find(x + n) == find(y)) cnt++;
else
{
Union(x, y);
Union(x + n, y + n);
Union(x + 2 * n, y + 2 * n);
}
}
else if (find(x) == find(y) || find(y) == find(x + n)) cnt++;
else
{
Union(x, y + n);
Union(x + n, y + 2 * n);
Union(x + 2 * n, y);
}
}
cout << cnt;
return 0;
}

