正则化
正则化是为了减小泛化误差而对算法进行的修改
有的正则化是给模型施加额外的限制条件，例如限制参数值范围；有些是在目标函数中添加一些额外惩罚项，本质上也是希望限制参数值。
常见的正则化方法有：
Parameter Norm Penalties
在目标函数中调价对参数的惩罚项。
$$\tilde{J}\left(\theta;X,y\right)=J(\theta;X,y)+\alpha\Omega(\theta)$$
其中$\alpha \in [0,\infty)$ ，取0时，正则项为0，取得越大，正则化效果越大。
由于加入了关于参数大小的惩罚项，模型训练过程不仅仅是要减小训练集上的损失函数，而且也要保持惩罚项尽量小，比如L1 regularization和L2 regularization
其中L2 regularization：
又被称为权重衰减 weight decay。通过添加$\operatorname{}\Omega(\theta)=\frac12||w||_2^2$的正则项，可以使得权重减小。原因如下：
每次梯度下降的时候，对于损失函数$\tilde{J}\left(w;X,y\right)=J(w;X,y)+\frac\alpha2w^Tw$求梯度，得到$\triangledown_w\tilde{J}\left(w;X,y\right)=\triangledown_wJ(w;X,y)+\alpha w$，这样在更新的时候，$w\leftarrow(1-\epsilon\alpha)w-\epsilon\triangledown_wJ(w;X,y)$。这样的话，每次更新参数，都会有一个常数的衰减。
其中L1 regularization：
不同于L2，L1是加入了对于每一个元素的绝对值的求和惩罚项$\Omega(\theta)=\left|\left|w\right|\right|_1=\sum_i\left|w_i\right|$，那么损失函数变为：$\tilde{J}\left(w;X,y\right)=J(w;X,y)+\alpha||w||_1$。
那么求梯度：$\triangledown_w\tilde{J}\left(w;X,y\right)=\triangledown_wJ(w;X,y)+\alpha sign(w)$，$sign$是正负号函数。
那么对比L1和L2：
L1使权重更稀疏(sparse)，即使很多项最优值为零，而对应的L2仅是使权重更小而不为零。
由于L1稀疏化的性质常常被用来做特征选择(feature selection)，因为它可以使某些权重为零，说明相对应的特征可以安全地忽略掉
dataset augmentation
数据增强，就是提供更多的训练数据。当然实际操作中，有时候训练集是有限的，我们可以制造一些假数据并添加入训练集中，比如对图像的旋转平移等。希望模型能够在这些变换或干扰不受影响保持预测的准确性，从而减小泛化误差。
多任务学习
与Dataset augmentation类似，多任务学习也是希望令模型的参数能够进行很好的泛化，其原理是对多个目标共享模型的一部分（输入及某些中间的表示层），使其对于多个有关联的目标均有较好的效果，保证模型可以更好的推广。
早停策略 early stopping
通常对于较大的模型，我们会观察到训练集上的误差不断减小，但验证集上的误差会在某个点之后反而逐渐增大，这意味着为了减小泛化误差，我们可以在训练过程中不断的记录验证集上的误差及对应的模型参数，最终返回验证集上误差最小所对应的模型参数，这个简单直观的方法就是early stopping。
这个策略我在做毕设的时候也用到了，核心会设置一个patience参数，表示验证集连续多少次指标下降会停止训练。
dropout
如果模型的参数太多，而训练样本又太少，训练出来的模型很容易产生过拟合的现象。在训练神经网络的时候经常会遇到过拟合的问题，过拟合具体表现在：模型在训练数据上损失函数较小，预测准确率较高；但是在测试数据上损失函数比较大，预测准确率较低。
Dropout可以作为训练深度神经网络的一种trick供选择。在每个训练批次中，通过忽略一半的特征检测器（让一半的隐层节点值为0），可以明显地减少过拟合现象。这种方式可以减少特征检测器（隐层节点）间的相互作用，检测器相互作用是指某些检测器依赖其他检测器才能发挥作用。
Dropout说的简单一点就是：我们在前向传播的时候，让某个神经元的激活值以一定的概率p停止工作，这样可以使模型泛化性更强，因为它不会太依赖某些局部的特征。
具体的操作：
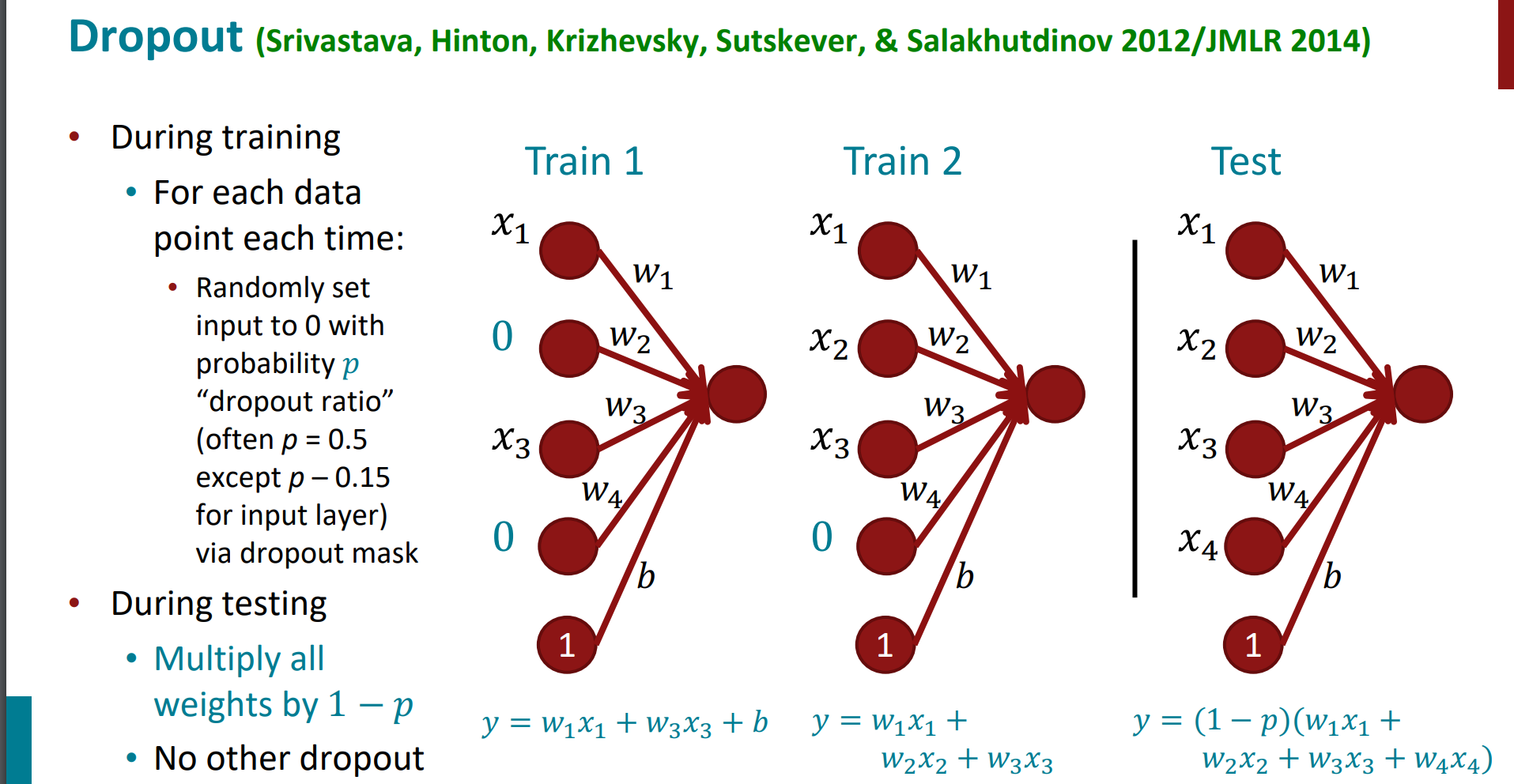
- 首先随机（临时）删掉网络中一半的隐藏神经元，输入输出神经元保持不变
- 然后把输入x通过修改后的网络前向传播，然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后，在没有被删除的神经元上按照随机梯度下降法更新对应的参数（w，b）。
那么dropout具体如何实现呢？（这个后面专门出一篇进行dropout的整理，这里就简单了解~）
vectorization
能用向量/矩阵乘法的，就不要用循环，这样会极大提升运算速度。
随机初始化参数的重要性
非线性函数的递进（激活函数）
我们最先接触的是logistic的，又叫sigmoid函数。映射到了0-1之间。
$$f(z)=\frac{1}{1+\exp(-z)}$$
之后，我们接触到了双曲正切函数tanh，其实也是sigmoid函数通过数学运算演变而来。
$$\tanh(z)=2\mathrm{logistic}(2z)-1$$
但指数运算的缺点，就是计算量大，计算速度下来了，又出来了hard tanh
$$\left.\text{HardTanh}(x)=\left\{\begin{array}{cl}-1&\text{if}x<-1\\x&\text{if}-1<=x<=1\\1&\text{if}x>1\end{array}\right.\right.$$
然后又提出了目前应用最多最广泛的ReLu
$$\mathrm{rect}(z)=\max(z,0)$$
优化器optimizers
目前最常用的应该是Adam机器变种AdamW
学习率的选择
可以用恒定的学习率，也可以去训练学习率不断下降
大概就是这些，常用的还是L1,L2和dropout
