回顾欧拉函数

首先它是基于线性筛素数的,只是稍加改造

void get_eular(int n){
    phi[1]=1;
    for(int i=2;i<=n;i++){
        if(!st[i]) {
            primes[cnt++]=i;
            phi[i]=i-1;//i是质数,与i互质的个数有i-1个(包括1)
        }
        for(int j=0;primes[j]<=n/i;j++){
            st[primes[j]*i]=true;//一定要先标记合数
            if(i%primes[j]==0){
                phi[i*primes[j]]=primes[j]*phi[i];//求pj*i的欧拉函数
                break;//找到最小质因数退出
            }
                phi[primes[j]*i]=phi[i]*(primes[j]-1);//求pj*i的欧拉函数
            //这一步不可以提到标记合数后,因为要先看可不可以被primes[j]整除,如果不可以才执行这一步
            //否则会phi两次
        }
    }

}

注意

欧拉函数是积性函数,当题目让你求的式子中有两个欧拉函数相乘
可以考虑积性函数的性质

题目

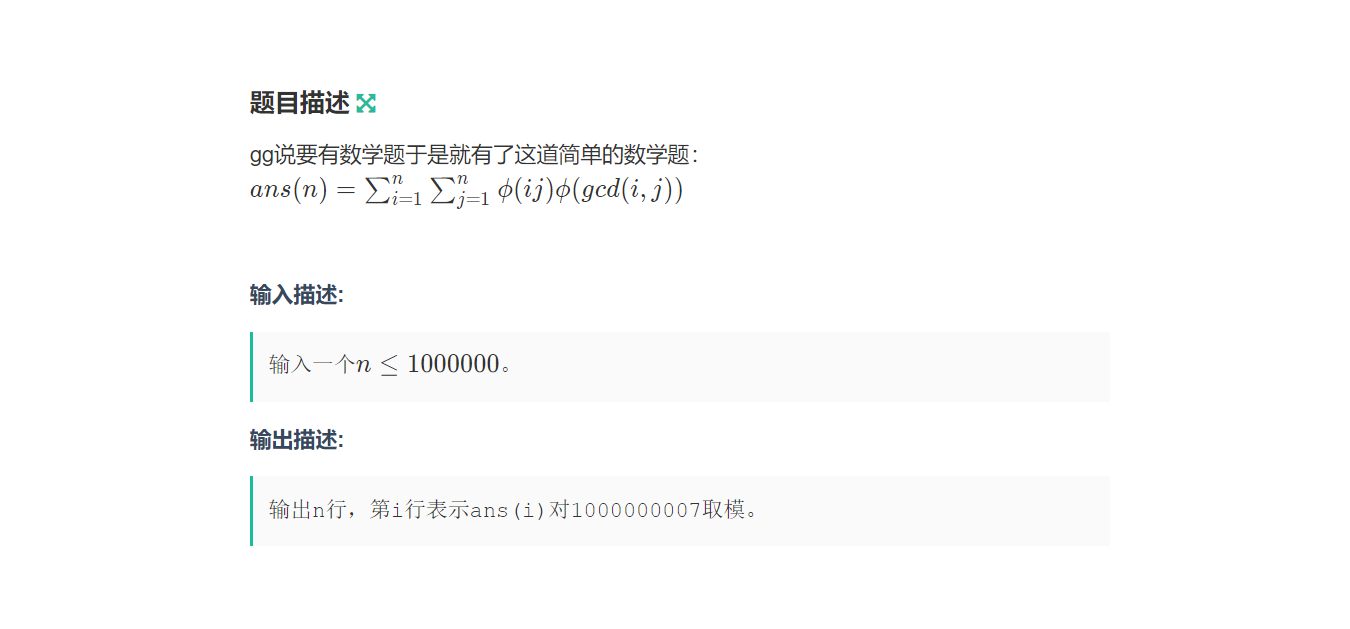
不会mardown语法(qwq)

分析

首先这里面有一个欧拉函数是两个数i,j乘积的形式,可以用积性函数的性质拆开来
于是有下图

本来应该是i,j,这两个控制gcd(i,j)的值,现在变成了d=gcd(i,j)去控制i,j的值,这样省去了一个gcd
函数也使得时间复杂度降下来.然后对于[n,n+d-1]这个区间,d|n,d!|n+1,所以在第一维是d的时候n+1其实不会被
循环到,这样其实就f[n+1]在d的时候的值是f[n]贡献的!!!

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define read(x) scanf("%d",&x)
#define write(x) printf("%d\n",&x)
const int N =1e6+10,mod=1e9+7;
int n;
int primes[N],cnt,phi[N],st[N];
ll f[N];
void init()
{
    phi[1]=1;
    for(int i=2;i<=N;i++)
    {
        if(!st[i])  
        {
            primes[cnt++]=i;
            phi[i]=i-1;
        }
        for(int j=0;j<=cnt&&(ll)primes[j]*i<=N;j++)
        {
            st[primes[j]*i]=true;
            if(i%primes[j]==0)  
            {
                phi[primes[j]*i]=primes[j]*phi[i];
                break;
            }
            phi[primes[j]*i]=(primes[j]-1)*phi[i];//不能整除的情况
        }
    }
}
int main()
{
    read(n);
    init();
    for(int d=1;d<=N;d++)
    {
        ll ss=0;
        for(int n=d;n<=N;n+=d)
        {
            ss=(ss+phi[n])%mod;//这是求欧拉函数和phi[d]+phi[2*d]+....
            ll x=ss*ss%mod*phi[d]%mod;//求在gcd(i,j)等d时的公式值
            int l=n,r=n+d;
            f[l]=(f[l]+x)%mod;//差分
            if(r>=N) continue;//不能越界
            f[r]=((f[r]-x)%mod+mod)%mod;//差分
        }
    }

    for(int i=1;i<=N;i++)   f[i]=(f[i]+f[i-1])%mod;

    for(int i=1;i<=n;i++)   printf("%lld\n",f[i]);

}