题意是问是否只有一个章鱼子图（章鱼图是只有一个环+若干枝（可以为0个）的无向连通图），这里的章鱼子图是指图中的一个连通块是否是一个章鱼图，所以将给定图分成几个连通块来判断即可（dfs遍历，如果一个点会被遍历2次即以上，则存在环）

#include <bits/stdc++.h>
using namespace std;
const int N=100010,M=2*N;   //注意无向边
int h[N],e[M],ne[M],idx;
int d[N];   //存储每个顶点的深度，环内顶点与相反遍历方向的顶点的深度差+1为顶点个数
bool st[N];   //存储每个点是否被遍历过，如果一个点被dfs2次及以上，说明存在环
int uc,mx;  //uc代表每个连通块中环个数的两倍  mx代表每个环的顶点个数

void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

//不回头遍历的dfs
void dfs(int u,int fa)
{
    st[u]=1;
    for(int i=h[u];~i;i=ne[i])
    {
        int j=e[i];
        if(j==fa)    continue;
        if(!st[j]){   
            d[j]=d[u]+1;
            dfs(j,u);
        }
        else{
            uc++;
            mx=abs(d[j]-d[u])+1;
        }
    }
}


void solve()
{
    //每个样例要重新初始化
    idx=0;
    memset(h,-1,sizeof h);
    memset(st,0,sizeof st);
    memset(d,0,sizeof d);


    int n,m;cin>>n>>m;
    while(m--)
    {
        int a,b;cin>>a>>b;
        add(a,b),add(b,a);
    }

    int cnt=0;  //章鱼子图的个数
    for(int i=1;i<=n;i++){
        //对于每个连通块单独判断是否为章鱼图，再计数
        if(!st[i]){
            uc=0;
            dfs(i,-1);
            uc/=2;
            if(uc==1)    cnt++;
        }
    }

    if(cnt==1)    cout<<"Yes "<<mx<<endl;
    else    cout<<"No "<<cnt<<endl;
}

int main()
{
    int t;cin>>t;
    while(t--)    solve();
    return 0;
}

#include <bits/stdc++.h>
using namespace std;
int f[5010];   //f的含义是所选的工作方案在前i个工作中，在j时结束的最大报酬
struct node
{
    int t,d,p;
}a[5010];

//贪心排序
bool cmp(node a,node b)
{
    if(a.d!=b.d)    return a.d<b.d;  //结束时间
    else if(a.t!=b.t)    return a.t<b.t;  //所需时间
    else    return a.p>b.p;  //报酬
}

void solve()
{
    memset(f,0,sizeof f);
    int n;cin>>n;
    int mx=0;
    for(int i=1;i<=n;i++){
        cin>>a[i].t>>a[i].d>>a[i].p;
    }    

    sort(a+1,a+1+n,cmp);

    //01背包，滚动数组
    for(int i=1;i<=n;i++){
        //这个工作可能完成时
        if(a[i].t<=a[i].d){
            //枚举该工作可能完成的时间
            for(int j=a[i].d;j>=a[i].t;j--){
                //选与不选取较大值
                f[j]=max(f[j],f[j-a[i].t]+a[i].p);
            }
        }

    }

    //在不同时间结束代表不同的方案，取最大值的那个方案
    for(int i=0;i<=5000;i++){
        if(f[i]>mx){
            mx=f[i];
        }    

    }
    cout<<mx<<endl;
}

int main()
{
    int t;cin>>t;
    while(t--)    solve();
    return 0;
}

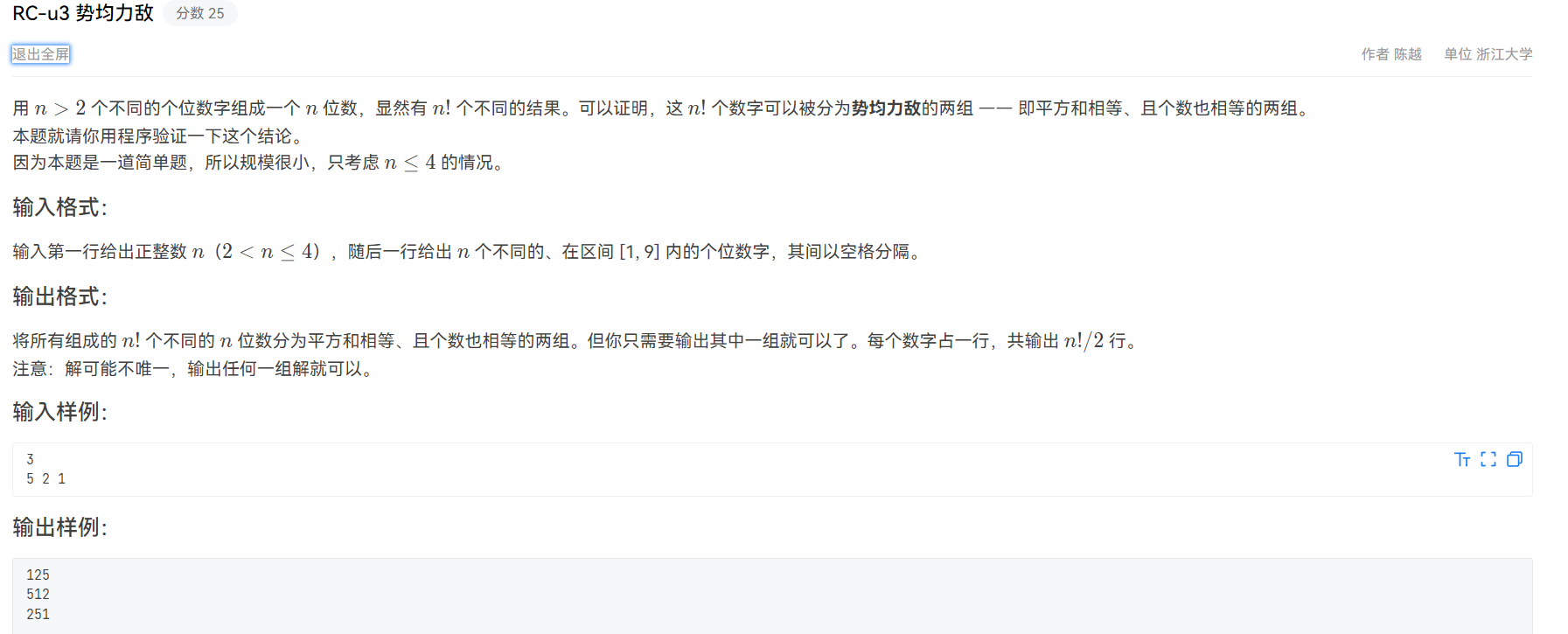
排列枚举+组合枚举

#include <bits/stdc++.h>
using namespace std;
int a[5];
int b[30];

int n;
int k=0,sum=0;
int c[15];

void dfs(int u,int start)
{ 
    if(u+k-start<k/2)   return;
    if(u==k/2){
        int s=0;
        for(int i=0;i<k/2;i++)  s+=c[i]*c[i];
        if(s==sum/2){
            for(int i=0;i<k/2;i++)  cout<<c[i]<<endl;
            exit(0);
        }
        return;     //不能忘记返回，否则会无限递归
    }

    for(int i=start;i<k;i++){
        c[u]=b[i];
        dfs(u+1,i+1);
    }
}

int main()
{
   cin>>n;
    for(int i=0;i<n;i++)    cin>>a[i];
    sort(a,a+n);

    do{
        int t=0;
        for(int i=0;i<n;i++){
            t=t*10+a[i];
        }
        b[k++]=t;
        sum+=t*t;
    }while(next_permutation(a,a+n));
    dfs(0,0);
    return 0;
}

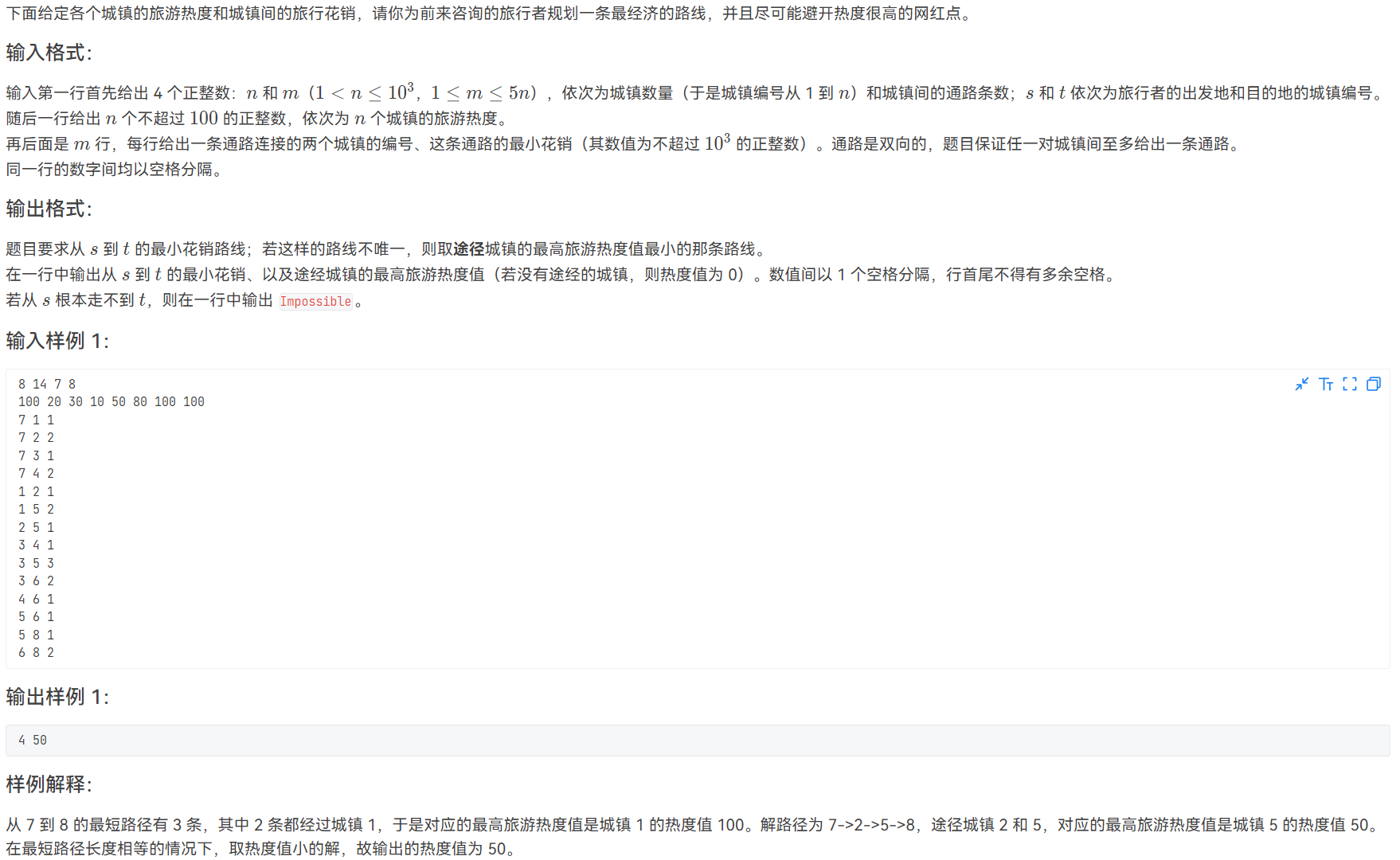
spfa处理多重条件选择最短路

#include <bits/stdc++.h>
using namespace std;
const int N=1010,inf=0x3f3f3f3f;
struct pii{
  int v,w;  
};
vector<pii>e[N];
int h[N],d[N];
int r[N];   //存储到达i点途径的最高热度值（不包括i点）
bool st[N];
int n,m,s,t;

void spfa()
{
    memset(d,inf,sizeof d);
    queue<int>q;
    q.push(s);
    d[s]=0;
    r[s]=h[s]=0;  //要求输出的是途径的城市的最高热度，避免得到起点热度值
    st[s]=1;

    while(q.size())
    {
        int u=q.front();q.pop();
        st[u]=0;

        for(auto ed:e[u]){
            int v=ed.v,w=ed.w;
            if(d[u]+w==d[v]){  //当花销一样时
                int x=max(r[u],h[u]);
                if(x<r[v]){  //如果新路线的最高热度值低
                    r[v]=x;
                }
            }    
            else if(d[u]+w<d[v]){
                r[v]=max(h[u],r[u]);
                d[v]=d[u]+w;
                if(!st[v])    q.push(v),st[v]=1;
            }
            //不能写if(v==t)    break;
            //因为t的最短路在后面可能会更新
        }
    }
    if(d[t]==inf)    puts("Impossible");
    else    cout<<d[t]<<' '<<r[t];
}


int main()
{
    cin>>n>>m>>s>>t;
    for(int i=1;i<=n;i++)    cin>>h[i];
    while(m--)
    {
        int x,y,z;cin>>x>>y>>z;
        e[x].push_back({y,z});
        e[y].push_back({x,z});
    }

    spfa();
    return 0;
}

二维前缀和

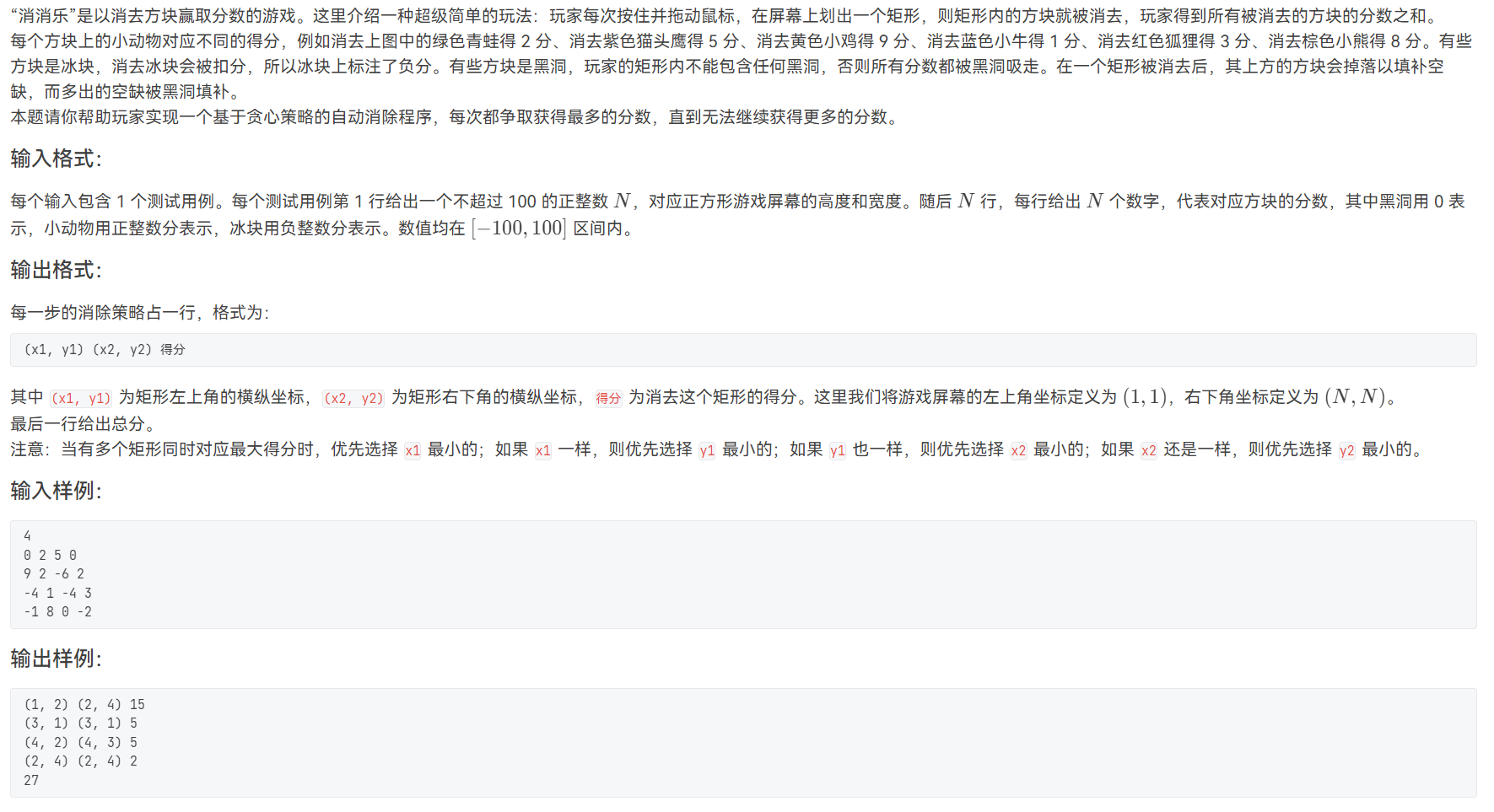
注意题目输入的是按横向是x轴与二维矩阵里的x与y相反，所以输入时输入原矩阵的转置矩阵，这样就实现xy轴与二维矩阵里xy一致。

#include <iostream>
using namespace std;
const int N=110;
int a[N][N];
int b[N][N],c[N][N];  //分数前缀和   黑洞个数前缀和
int n;

void inita(int x1,int y1,int x2,int y2)  //更新方块移动后的矩阵
{
    for(int i=x1;i<=x2;i++){
        for(int j=y2;j>=1;j--){  //更新1~y2的所有方块
            int len=y2-y1+1;  //一行消除的方块数
            if(j-len<1)    a[i][j]=0;
            else    a[i][j]=a[i][j-len];
        }
    }
}



void initb()
{
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            b[i][j]=a[i][j]+b[i-1][j]+b[i][j-1]-b[i-1][j-1];
}

void initc()
{
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            int x;  //a[i][j]黑洞的个数
            if(a[i][j]==0)    x=1;
            else x=0;
            c[i][j]=x+c[i-1][j]+c[i][j-1]-c[i-1][j-1];
        }
    }
}

int askb(int x1,int y1,int x2,int y2)
{
    return b[x2][y2]-b[x2][y1-1]-b[x1-1][y2]+b[x1-1][y1-1];
}

int askc(int x1,int y1,int x2,int y2)
{
    return c[x2][y2]-c[x2][y1-1]-c[x1-1][y2]+c[x1-1][y1-1];
}

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            cin>>a[j][i];

    int tot=0;
    initb(),initc();   //先初始化完成第一次
    while(1)
    {
        int ans=0,x1,y1,x2,y2;
        //暴力枚举子矩阵
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                for(int k=i;k<=n;k++){
                    for(int l=j;l<=n;l++){
                        if(askc(i,j,k,l)>0)    break;
//若矩阵(i,j)(k,l)有黑洞，则矩阵(i,j)(k,l+1)也一定会有黑洞（包含关系）
                        if(askb(i,j,k,l)>ans){
                            ans=askb(i,j,k,l);
                            x1=i,y1=j,x2=k,y2=l;
                        }
                    }
                }
            }
        }
        if(ans==0)    break;
        printf("(%d, %d) (%d, %d) %d\n",x1,y1,x2,y2,ans);
        tot+=ans;
        inita(x1,y1,x2,y2);  //更新矩阵
        initb(),initc();
    }
    cout<<tot;
    return 0;
}