我们开始新的知识喽！

（好吧，是我们熟知的反向传播，那我们就快一些吧hhh）

回顾一下雅各比矩阵吧：

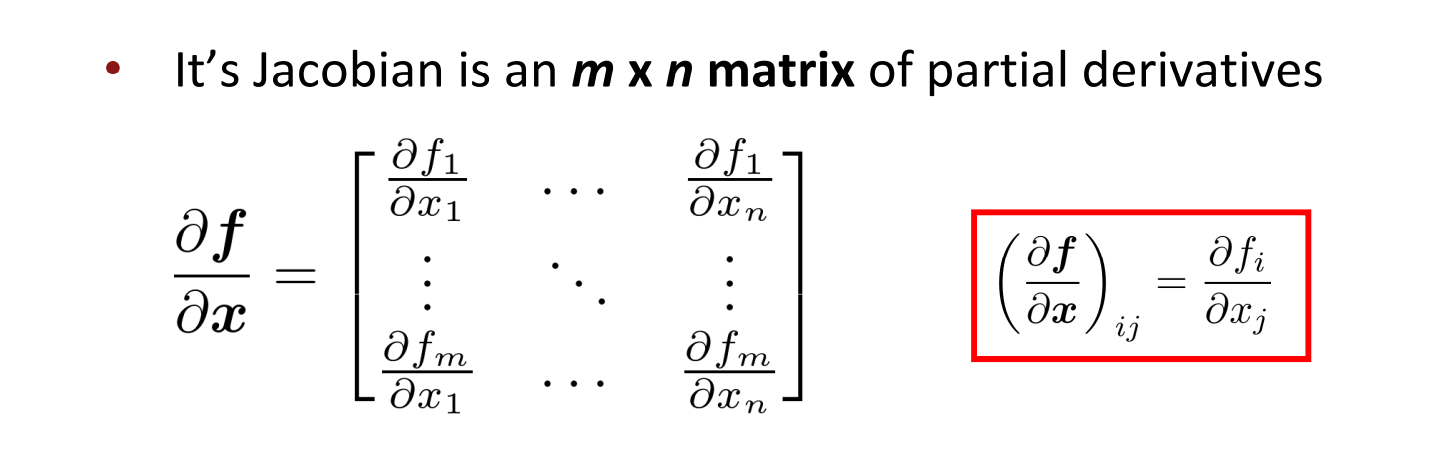
这里我们注意一个公式的推导，即下图：

这一讲主要就是聚焦于反向传播，那么核心是数学的求导。我们就详细把矩阵求导的本质理解透吧。

矩阵求导的布局约定

我们以一个抽象表示的函数为例

$$\text{function(input)}$$

根据函数function和输入input的类型不同，分成不同的种类

function是标量

1. input是标量
   这种情况是最常见的，那就是我们高数常用的普通求导。如下所示
   $$f(x)=x+1$$
2. input是向量
   此时，函数的自变量x是向量，表示为$\boldsymbol{x}=[x_1,x_2,x_3]^T$，那么此时函数可以是
   $$f(\boldsymbol{x})=a_1x_1^2+a_2x_2^2+a_3x_3^2+a_4x_1x_2$$

通俗理解就是这里的输入$x$有很多列方向的分量

1. input是matrix
   此时设输入input矩阵为$\boldsymbol{X}_{3\times2}=(x_{ij})_{i=1,j=1}^{3,2}$，那么函数可以表示为：
   $$f(\boldsymbol{X})=a_1x_{11}^2+a_2x_{12}^2+a_3x_{21}^2+a_4x_{22}^2+a_5x_{31}^2+a_6x_{32}^2$$

这里比较好理解的是，输入$x$是有行和列的分量
这都是函数本身是标量的情况。

function是向量

此时，$\boldsymbol f$是有若干个f组成的向量

通俗理解就是函数$f$有很多个小的$f_i$组成的

1. 输入input是标量
   那么此时函数可以表示为
   $$\boldsymbol{f}_{3\times1}(x)=\begin{bmatrix}f_1(x)\\f_2(x)\\f_3(x)\end{bmatrix}=\begin{bmatrix}x+1\\2x+1\\3x^2+1\end{bmatrix}$$

这里通俗理解就是，每一个输入的x没有分量，就是单纯的x

1. 输入input是向量
   设此时$\boldsymbol{x}=[x_1,x_2,x_3]^T$。那么函数可以表示为

这里通俗理解的是，输入的x也是列方向很多的小分量，同时带入多个函数$f_i$的分量。

$$\boldsymbol{f}_{3\times1}(\boldsymbol{x})=\begin{bmatrix}f_1(\boldsymbol{x})\\f_2(\boldsymbol{x})\\f_3(\boldsymbol{x})\end{bmatrix}=\begin{bmatrix}x_1+x_2+x_3\\x_1^2+2x_2+2x_3\\x_1x_2+x_2+x_3\end{bmatrix}$$

1. 输入input是矩阵
   设此时$\boldsymbol{X}_{3\times2}=(x_{ij})_{i=1,j=1}^{3,2}$

那么函数可以表达为

$$\left.\boldsymbol{f}_{3\times1}(\boldsymbol{X})=\begin{bmatrix}f_1(\boldsymbol{X})\\f_2(\boldsymbol{X})\\f_3(\boldsymbol{X})\end{bmatrix}=\left[\begin{array}{c}x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}\\x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}+x_{11}x_{12}\\2x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}+x_{11}x_{12}\end{array}\right.\right]$$

通俗理解为，输入有行和列的分量$x_{11},x{12}…$ ，同时多个函数的列分量$f_i$

function是矩阵

函数F是由很多分量$f$组成的，如$f_{11},f_{12}…$

1. 输入是标量
   这种情况就是很多个函数，但只有单变量x
   $$\boldsymbol{F}_{3\times2}(x)=\begin{bmatrix}f_{11}(x)&f_{12}(x)\\f_{21}(x)&f_{22}(x)\\f_{31}(x)&f_{32}(x)\end{bmatrix}=\begin{bmatrix}x+1&2x+2\\x^2+1&2x^2+1\\x^3+1&2x^3+1\end{bmatrix}$$

2. 输入input是向量
   设$\boldsymbol{x}=[x_1,x_2,x_3]^T$

这样的话，就是很多个函数$f_{ij}$，同时有很多个变元$x_{ij}$

$$\boldsymbol{F}_{3\times2}(\boldsymbol{x})=\begin{bmatrix}f_{11}(\boldsymbol{x})&f_{12}(\boldsymbol{x})\\f_{21}(\boldsymbol{x})&f_{22}(\boldsymbol{x})\\f_{31}(\boldsymbol{x})&f_{32}(\boldsymbol{x})\end{bmatrix}=\begin{bmatrix}2x_1+x_2+x_3&2x_1+2x_2+x_3\\2x_1+2x_2+x_3&x_1+2x_2+x_3\\2x_1+x_2+2x_3&x_1+2x_2+2x_3\end{bmatrix}$$

1. 输入input是矩阵
   设$\boldsymbol{X}_{3\times2}=(x_{ij})_{i=1,j=1}^{3,2}$

这样的话，就是很多个函数$f_{ij}$，同时一个矩阵的变元$x_{ij}$

$$\begin{aligned} F_{3\times2}(\boldsymbol{X})& =\begin{bmatrix}f_{11}(\boldsymbol{X})&f_{12}(\boldsymbol{X})\\f_{21}(\boldsymbol{X})&f_{22}(\boldsymbol{X})\\f_{31}(\boldsymbol{X})&f_{32}(\boldsymbol{X})\end{bmatrix} \\ &=\left[\begin{array}{cc}x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}&2x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}\\3x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}&4x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}\\5x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}&6x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}\end{array}\right] \end{aligned}$$

矩阵求导的本质

求导本质就是本质就是$F$中的每个$f$分别对变元中的每个元素逐个求偏导，只不过写成了向量、矩阵形式而已。

我们可以以这个为例：
$$f(x_1,x_2,x_3)=x_1^2+x_1x_2+x_2x_3$$

分别求偏导，得到如下：

$$\begin{cases}\frac{\partial f}{\partial x_1}=2x_1+x_2\\\\\frac{\partial f}{\partial x_2}=x_1+x_3\\\\\frac{\partial f}{\partial x_3}=x_2\end{cases}$$

写成列向量的形式：

$$\frac{\partial f(\boldsymbol{x})}{\partial\boldsymbol{x}_{3\times1}}=\begin{bmatrix}\frac{\partial f}{\partial x_1}\\\frac{\partial f}{\partial x_2}\\\frac{\partial f}{\partial x_3}\end{bmatrix}=\begin{bmatrix}2x_1+x_2\\x_1+x_3\\x_2\end{bmatrix}$$

当然，也可以写成行向量，都可以的

$$\frac{\partial f(\boldsymbol{x})}{\partial\boldsymbol{x}_{3\times1}^T}=\left[\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\frac{\partial f}{\partial x_3}\right]=[2x_1+x_2,x_1+x_3,x_2]$$

那么我们就可以得出：

如果函数$f$有$m$个，变元中有n个元素，那么求偏导后，就有$m \times n$个元素。

矩阵求导结果的布局

分子布局

分子，也就是函数f，是列向量；分母，也就是自变量x，是行向量

$$\frac{\partial\boldsymbol{f}_{2\times1}(\boldsymbol{x})}{\partial\boldsymbol{x}_{3\times1}^T}=\begin{bmatrix}\frac{\partial f_1}{\partial x_1}&\frac{\partial f_1}{\partial x_2}&\frac{\partial f_1}{\partial x_3}\\\frac{\partial f_2}{\partial x_1}&\frac{\partial f_2}{\partial x_2}&\frac{\partial f_2}{\partial x_3}\end{bmatrix}_{2\times3}$$

分母布局

分子，也就是函数f，是行向量；分母，也即是自变量x，是列向量

$$\frac{\partial\boldsymbol{f}_{2\times1}^T(\boldsymbol{x})}{\partial\boldsymbol{x}_{3\times1}}=\begin{bmatrix}\frac{\partial f_1}{\partial x_1}&\frac{\partial f_2}{\partial x_1}\\\frac{\partial f_1}{\partial x_2}&\frac{\partial f_2}{\partial x_2}\\\frac{\partial f_1}{\partial x_3}&\frac{\partial f_2}{\partial x_3}\end{bmatrix}_{3\times2}$$

其实这里的布局，无非就是分子的转置、向量化，分母的转置、向量化，它们的各种组合而已。

这里我们其实是完成了先导部分，正式开始矩阵求导公式的数学推导吧！

变元是向量

$$f(\boldsymbol{x}),\boldsymbol{x}=[x_1,x_2,\cdots,x_n]^T$$

1. 常数求导
   此时函数为常函数，那么结果为零向量

$$\frac{\partial c}{\partial\boldsymbol{x}}=\mathbf{0}_{n\times1}$$

证明过程：
$$\begin{aligned}\frac{\partial c}{\partial\boldsymbol{x}}&=\begin{bmatrix}\frac{\partial c}{\partial x_1}\\\frac{\partial c}{\partial x_2}\\\vdots\\\frac{\partial c}{\partial x_n}\end{bmatrix}\\\\&=\begin{bmatrix}0\\0\\\vdots\\0\end{bmatrix}\\\\&=\mathbf{0}_{n\times1}\end{aligned}$$

1. 线性法则
   与一元函数求导线性法则相同：相加再求导等于求导再相加，常数提外面
   $$\frac{\partial[c_1f(\boldsymbol{x})+c_2g(\boldsymbol{x})]}{\partial\boldsymbol{x}}=c_1\frac{\partial f(\boldsymbol{x})}{\partial\boldsymbol{x}}+c_2\frac{\partial g(\boldsymbol{x})}{\partial\boldsymbol{x}}$$

证明：

$$\begin{aligned} \frac{\partial[c_1f(\boldsymbol{x})+c_2g(\boldsymbol{x})]}{\partial x}& \left.=\left[\begin{array}{c}\frac{\partial(c_1f+c_2g)}{\partial x_1}\\\frac{\partial(c_1f+c_2g)}{\partial x_2}\\\vdots\\\frac{\partial(c_1f+c_2g)}{\partial x_n}\end{array}\right.\right] \\ &=\begin{bmatrix}c_1 \frac{\partial f}{\partial x_1} + c_2 \frac{\partial g}{\partial x_1}\\\\c_1 \frac{\partial f}{\partial x_2} + c_2 \frac{\partial g}{\partial x_2}\\\\\vdots\\c_1 \frac{\partial f}{\partial x_n} + c_2 \frac{\partial g}{\partial x_n}\end{bmatrix} \\ &=c_1\begin{bmatrix}\frac{\partial f}{\partial x_1}\\\frac{\partial f}{\partial x_2}\\\vdots\\\frac{\partial f}{\partial x_n}\end{bmatrix}+c_2\begin{bmatrix}\frac{\partial g}{\partial x_1}\\\frac{\partial g}{\partial x_2}\\\vdots\\\frac{\partial g}{\partial x_n}\end{bmatrix} \\ &=c_1\frac{\partial f(\boldsymbol{x})}{\partial\boldsymbol{x}}+c_2\frac{\partial g(\boldsymbol{x})}{\partial\boldsymbol{x}} \end{aligned}$$

1. 乘积法则
   与一元函数求导乘积法则相同：前导后不导 加 前不导后导

$$\frac{\partial[f(\boldsymbol{x})g(\boldsymbol{x})]}{\partial\boldsymbol{x}}=\frac{\partial f(\boldsymbol{x})}{\partial\boldsymbol{x}}g(\boldsymbol{x})+f(\boldsymbol{x})\frac{\partial g(\boldsymbol{x})}{\partial\boldsymbol{x}}$$

证明：

$$\begin{aligned} \frac{\partial[f(\boldsymbol{x})g(\boldsymbol{x})]}{\partial\boldsymbol{x}}& =\begin{bmatrix}\frac{\partial(fg)}{\partial x_1}\\\frac{\partial(fg)}{\partial x_2}\\\vdots\\\frac{\partial(fg)}{\partial x_n}\end{bmatrix} \\ &\left.=\left[\begin{array}{c}\frac{\partial f}{\partial x_1}g+f\frac{\partial g}{\partial x_1}\\\frac{\partial f}{\partial x_2}g+f\frac{\partial g}{\partial x_2}\\\vdots\\\frac{\partial f}{\partial x_n}g+f\frac{\partial g}{\partial x_n}\end{array}\right.\right] \\ &=\left[\begin{array}{c}\frac{\partial f}{\partial x_1}\\\frac{\partial f}{\partial x_2}\\\vdots\\\frac{\partial f}{\partial x_n}\end{array}\right]g+f\left[\begin{array}{c}\frac{\partial g}{\partial x_1}\\\frac{\partial g}{\partial x_2}\\\vdots\\\frac{\partial g}{\partial x_n}\end{array}\right] \\ &=\frac{\partial f(\boldsymbol{x})}{\partial\boldsymbol{x}}g(\boldsymbol{x})+f(\boldsymbol{x})\frac{\partial g(\boldsymbol{x})}{\partial\boldsymbol{x}} \end{aligned}$$

1. 商的法则
   与一元函数求导商法则相同：（上导下不导 减 上不导下导）除以（下的平方）：
   $$\frac{\partial\left[\frac{f(\boldsymbol{x})}{g(\boldsymbol{x})}\right]}{\partial\boldsymbol{x}}=\frac1{g^2(\boldsymbol{x})}\left[\frac{\partial f(\boldsymbol{x})}{\partial\boldsymbol{x}}g(\boldsymbol{x})-f(\boldsymbol{x})\frac{\partial g(\boldsymbol{x})}{\partial\boldsymbol{x}}\right]\\\text{其中,}g(\boldsymbol{x})\neq0\text{ 。}$$

证明：

$$\begin{aligned} \frac{\partial\biggl[\frac{f(x)}{g(x)}\biggr]}{\partial x}& =\left[\begin{array}{c}\frac{\partial(\frac{f}{g})}{\partial x_{1}}\\\\\frac{\partial(\frac{f}{g})}{\partial x_{2}}\\\vdots\\\frac{\partial(\frac{f}{g})}{\partial x_{n}}\end{array}\right] \\ &=\begin{bmatrix}\frac{1}{g^{2}}\left(\frac{\partial f}{\partial x_{1}}g-f\frac{\partial g}{\partial x_{1}}\right)\\\frac{1}{g^{2}}\left(\frac{\partial f}{\partial x_{2}}g-f\frac{\partial g}{\partial x_{2}}\right)\\\vdots\\\frac{1}{g^{2}}\left(\frac{\partial f}{\partial x_{n}}g-f\frac{\partial g}{\partial x_{n}}\right)\end{bmatrix} \\ &=\frac{1}{g^2}\left(\begin{bmatrix}\frac{\partial f}{\partial x_1}\\\frac{\partial f}{\partial x_2}\\\vdots\\\frac{\partial f}{\partial x_n}\end{bmatrix}g-f\begin{bmatrix}\frac{\partial g}{\partial x_1}\\\frac{\partial g}{\partial x_2}\\\vdots\\\frac{\partial g}{\partial x_n}\end{bmatrix}\right) \\ &=\frac{1}{g^{2}(\boldsymbol{x})}\left[\frac{\partial f(\boldsymbol{x})}{\partial\boldsymbol{x}}g(\boldsymbol{x})-f(\boldsymbol{x})\frac{\partial g(\boldsymbol{x})}{\partial\boldsymbol{x}}\right] \end{aligned}$$

几个经典的公式：

1. $$\frac{\partial(\boldsymbol{x}^{T}\boldsymbol{a})}{\partial\boldsymbol{x}}=\frac{\partial(\boldsymbol{a}^{T}\boldsymbol{x})}{\partial\boldsymbol{x}}=\boldsymbol{a}$$
   其中$\alpha $为常数向量，$\boldsymbol{a}=(a_1,a_2,\cdots,a_n)^T$
   证明：
   $$\begin{aligned} \frac{\partial(\boldsymbol{x}^T\boldsymbol{a})}{\partial\boldsymbol{x}}& =\frac{\partial(\boldsymbol{a}^T\boldsymbol{x})}{\partial\boldsymbol{x}} \\ &=\frac{\partial(a_1x_1+a_2x_2+\cdots+a_nx_n)}{\partial\boldsymbol{x}} \\ &=\left[\begin{array}{c}\frac{\partial(a_1x_1+a_2x_2+\cdots+a_nx_n)}{\partial x_1}\\\frac{\partial(a_1x_1+a_2x_2+\cdots+a_nx_n)}{\partial x_2}\\\vdots\\\frac{\partial(a_1x_1+a_2x_2+\cdots+a_nx_n)}{\partial x_n}\end{array}\right] \\ &=\begin{bmatrix}a_1\\a_2\\\vdots\\a_n\end{bmatrix} \\ &=\boldsymbol{a} \end{aligned}$$

2. $$\frac{\partial(\boldsymbol{x}^{T}\boldsymbol{x})}{\partial\boldsymbol{x}}=2\boldsymbol{x}$$
   证明：
   $$\begin{aligned} \frac{\partial(\boldsymbol{x}^T\boldsymbol{x})}{\partial\boldsymbol{x}}& =\frac{\partial(x_1^2+x_2^2+\cdots+x_n^2)}{\partial\boldsymbol{x}} \\ &=\begin{bmatrix}\frac{\partial(x_1^2+x_2^2+\cdots+x_n^2)}{\partial x_1}\\\frac{\partial(x_1^2+x_2^2+\cdots+x_n^2)}{\partial x_2}\\\vdots\\\frac{\partial(x_1^2+x_2^2+\cdots+x_n^2)}{\partial x_n}\end{bmatrix} \\ &=\begin{bmatrix}2x_1\\2x_2\\\vdots\\2x_n\end{bmatrix} \\ &=2\begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix} \\ &=2\boldsymbol{x} \end{aligned}$$

之后的后续再更吧hh