偷来的思维导图 感觉不错

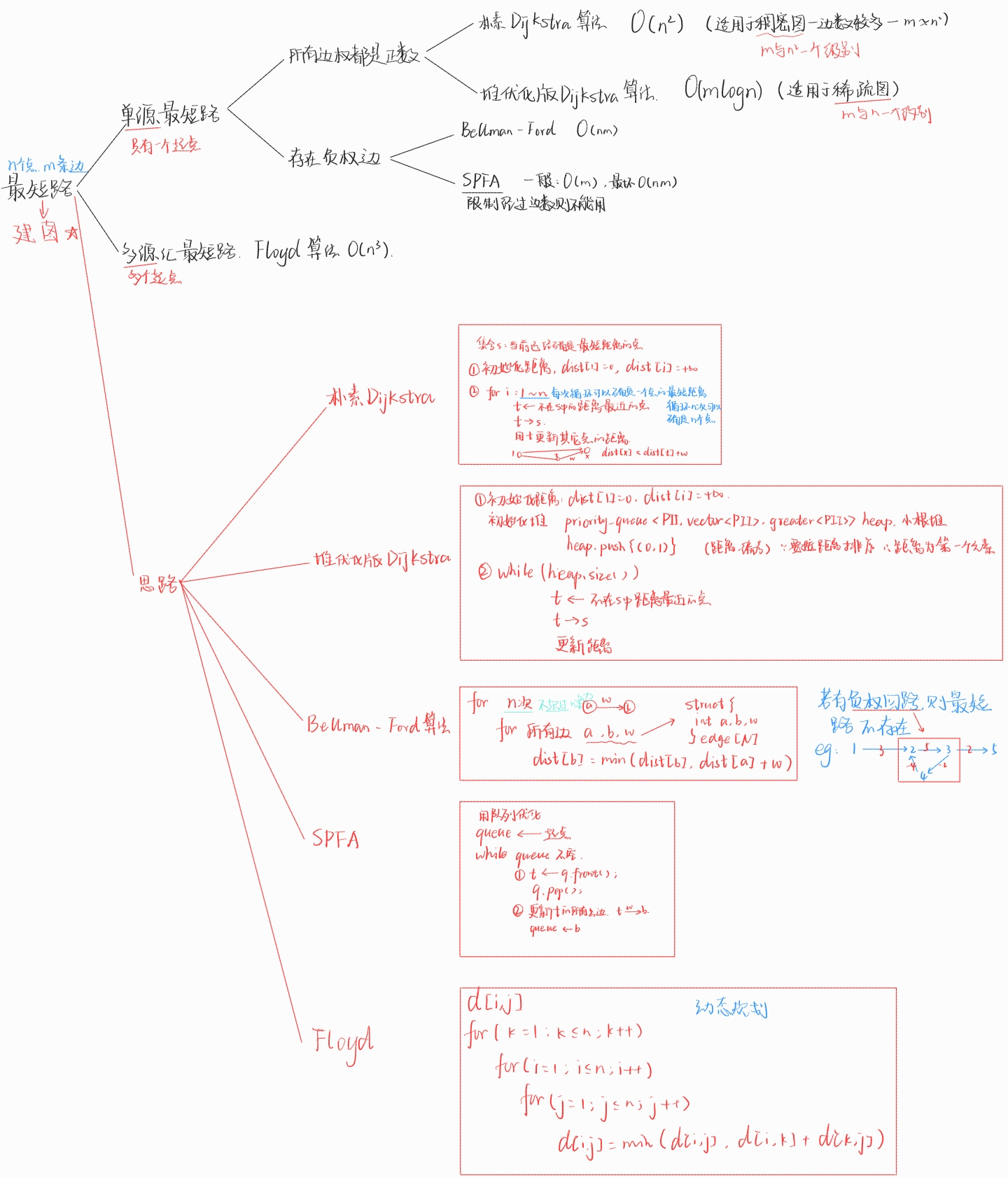
稠密图用邻接矩阵
伪代码：

int d[n],st[n];
d[1] = 0, st[1] = 1;
for(i:1 ~ n)
{
    t <- 没有确定最短路径的节点中距离源点最近的点;
    st[t] = 1;
    更新d;
}

#include<bits/stdc++.h>
using namespace std;
const int N=510;
#define int long long 
#define FAST ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define For(i, x) for (int i = 0; i < x; i++)
#define For1(i, x) for (int i = 1; i <= x; i++)
int g[N][N];//稠密图用邻接矩阵
int d[N];//距离
bool st[N];//状态
int n,m;
void dj(){
    memset(d,0x3f,sizeof d);
    d[1]=0;
    For(i,n){        //有n个点所以要进行n次 迭代
        int t=-1;        //存当前访问的点
                           最后为要找的当前距离源点最近的点 
                         //开局置为-1是为了先找到第一个没有确定的数
        for(int j=1;j<=n;j++)
            if(!st[j]&&(t==-1||d[t]>d[j]))
                t=j;
        st[t]=1;
        for(int j=1;j<=n;j++){
            d[j]=min(d[j],d[t]+g[t][j]);//原来的最短距离
                                        //当前点到该点的距离
        }

    }
}

signed main(){
    FAST
    cin>>n>>m;
    memset(g,0x3f,sizeof g);//初始化权重
    For(i,m){
        int x,y,z;
        cin>>x>>y>>z;
        g[x][y]=min(g[x][y],z);//保留短边
    }
    dj();
    if(d[n]==0x3f3f3f3f3f3f3f3f)cout<<"-1";
    else cout<<d[n];



    return 0;
}

稀疏图用邻接表(stl)
利用小顶堆（距离,编号） 每次弹出距离源点最近的点

#include<bits/stdc++.h>
using namespace std;
const int N=1.5e5+10;
#define int long long 
#define FAST ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define For(i, x) for (int i = 0; i < x; i++)
#define For1(i, x) for (int i = 1; i <= x; i++)
typedef pair<int, int> PII;
vector<PII>v[N];
int d[N],st[N];

void dj(){
    memset(d,0x3f,sizeof d);
    d[1]=0;
    priority_queue<PII, vector<PII>, greater<PII>>q;//小顶堆
    q.push({0,1});// 距离&节点 距离放前面 方便堆排序
    while(q.size()){
        auto t=q.top();
        q.pop();
        int node=t.second,len=t.first;//这里没用到 因为他就是d[node]
        if(st[node])continue;//定了就跳过
        st[node]=1;
        for(auto i:v[node]){
            int newnode=i.first,w=i.second;
            if(d[newnode]>d[node]+w){
                d[newnode]=d[node]+w;
                q.push({d[newnode],newnode});
            }
        }
    }



}
int n,m;
signed main(){
    FAST
    cin>>n>>m;
    For(i,m){
        int x,y,z;
        cin>>x>>y>>z;
        v[x].push_back({y,z});
    }
    dj();
    if(d[n]==0x3f3f3f3f3f3f3f3f)cout<<-1;
    else cout<<d[n];



    return 0;
}

练习：
https://www.acwing.com/problem/content/description/1377/

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
//#define int long long 
#define FAST ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define endl '\n'
#define For(i, x) for (int i = 0; i < x; i++)
#define For1(i, x) for (int i = 1; i <= x; i++)
typedef pair<int,int> PII;
int T,x,d[N],st[N];char n,m;
vector<PII>v[N];
int get(char x){
    if(x>='a'&&x<='z')return x-'a'+1;
    else return x-'A'+27;
}
void dij(){
    memset(d,0x3f,sizeof d);
    d[52]=0;
    priority_queue<PII,vector<PII>,greater<PII>>q;
    q.push({0,52});

    while(q.size()){
        auto t=q.top();q.pop();
        int node=t.second,len=t.second;
        if(st[node])continue;
        st[node]=1;
//      cout<<node<<endl;
        for(auto i:v[node]){
            int newnode=i.first,w=i.second;
//          cout<<newnode<<" ";
            if(d[newnode]>d[node]+w){
                d[newnode]=d[node]+w;
                q.push({d[newnode],newnode});
            }
        }
    }
}

signed main(){
    FAST
    cin>>T;
    while(T--){
        cin>>n>>m>>x;
        int nn=get(n),mm=get(m);
//      cout<<nn<<" "<<mm<<endl;
        v[nn].push_back({mm,x});
        v[mm].push_back({nn,x});
    }

    dij();
    int res=0x3f3f3f3f,ans=52;
    for(int i=27;i<=51;i++){
        if(d[i]<res){
            res=d[i];
            ans=i;
        }
    }

    cout<<char(ans-27+'A')<<" "<<res;


    return 0;
}