原题链接：3786. 二叉排序树

问题

分析

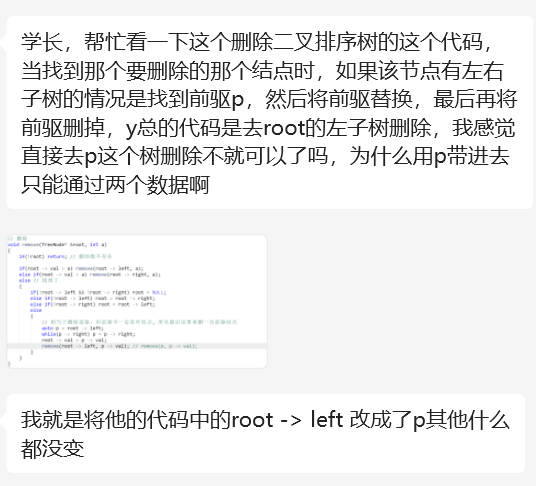
我们来看第43行的代码：

1. remove(root->left, p->val) 的含义

• root->left 是 root 的左子树。
• p->val 是前驱节点的值。
• 调用 remove(root->left, p->val) 意味着我们从 root 的左子树中删除这个前驱节点。

这个操作确保了我们在删除节点时，正确地调整了 root->left 这棵子树的结构。

2. remove(p, p->val) 的含义

• p 是 root->left 这棵子树中的一个节点，可能是其最右的节点。
• 调用 remove(p, p->val) 意味着我们从 p 开始的子树中删除值为 p->val 的节点。

这里的问题在于，如果你从 p 开始删除，这个操作不会影响 root->left 这个子树本身的结构。也就是说，虽然你删除了 p 节点，但 root->left 这个指针所指向的子树并没有得到正确的更新。

这其实这是一个经典的链表删除问题：

#include <iostream>

using namespace std;

struct Node
{
    int val;
    Node* next;
    Node(int x) : val(x), next(NULL) {}
};

void print(Node* head)
{
    for (auto p = head; p; p = p->next)
        cout << p->val << ' ';
    puts("");
}

int main() 
{
    Node *a = new Node(1), *b = new Node(2), *c = new Node(3);
    a->next = b;
    b->next = c;
    print(a);
    c = NULL;   // 这样并不会将c从链表中删除
    print(a);
    b->next = NULL; // 这样才会删除c
    print(a);   

    return 0;
}

输出

1 2 3 
1 2 3 
1 2 

将 c = NULL; 只是改变了指针 c 的值，它不再指向原来的节点 Node(3)，但原来 b->next 仍然指向那个节点。
在C++中，指针实际上是用来存储内存地址的变量。因此，当你创建一个指针（如 Node* c），它存储的是某个对象在内存中的地址。当你执行 c = NULL 时，你只是把指针 c 重新指向 NULL，也就是把 c 的值改为 NULL，但并没有影响到之前 c 所指向的那个内存位置（即链表中的节点）。

原题完整的正确代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int INF = 1e8;

// 二叉树结点的定义
struct TreeNode {
    int val;
    TreeNode *left, *right;
    TreeNode(int _val) : val(_val), left(NULL), right(NULL) {}
}* root;

// 插入结点操作
void insert(TreeNode* &root, int x) {
    if (!root) 
        root = new TreeNode(x);
    else if (x < root->val) 
        insert(root->left, x);
    else 
        insert(root->right, x);
}

// 删除结点操作
void remove(TreeNode* &root, int x) {
    if (!root) return;    // 如果删除的数不存在
    if (root->val == x) {
        if (!root->left && !root->right) 
            root = NULL; // 没有子节点，直接删除
        else if (!root->right) 
            root = root->left; // 只有左子节点
        else if (!root->left) 
            root = root->right; // 只有右子节点
        else {  
            // 左右儿子都存在的情况下，找到前驱结点（左子树中的最大值）
            TreeNode* p = root->left;
            while (p->right) 
                p = p->right;
            root->val = p->val;
            // p = NULL;   // 这里不能直接将p置为NULL，否则当p有左儿子会报错
            remove(root->left, p->val); // 递归删除前驱结点
        }
    } 
    else if (x > root->val) 
        remove(root->right, x);
    else 
        remove(root->left, x);
}

// 获取小于等于 x 的最大值
int get_pre(TreeNode* root, int x) {
    if (!root) 
        return -INF;
    else if (x <= root->val) 
        return get_pre(root->left, x);
    return max(root->val, get_pre(root->right, x));
} 

// 获取大于等于 x 的最小值
int get_post(TreeNode* root, int x) {
    if (!root) 
        return INF;
    else if (x >= root->val) 
        return get_post(root->right, x);
    return min(root->val, get_post(root->left, x));
}

int main() {
    int n;
    cin >> n;
    while (n --) {
        int t, x;
        cin >> t >> x;
        if (t == 1) 
            insert(root, x);
        else if (t == 2) 
            remove(root, x);
        else if (t == 3) 
            cout << get_pre(root, x) << endl;
        else 
            cout << get_post(root, x) << endl;
    }
    return 0;
}