历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

悟空都能学会的倍增求LCA

作者：

whale77 , 2024-08-22 21:49:18 , 所有人可见 , 阅读 110

17

4

倍增求LCA

（可新学，亦可复习）

水一次分享，望谅解（悟空：这年头你小子敢水，哼）

什么是LCA？

LCA（Least Common Ancestors），即最近公共祖先，是指在有根树中，找出某两个结点u和v最近的公共祖先。

当我们处理树上点与点关系的问题时（例如，最简单的，树上两点的距离），常常需要获知树上两点的最近公共祖先。

暴力求解LCA

求解点的LCA，我们先来讨论朴素的暴力O(N)做法。

我们需要知道每个点的深度，于是首先进行一趟dfs：

int dep[MAXN];
bool vis[MAXN];
void dfs(int cur, int fath = 0) 
{
    if (vis[cur])
        return;
    vis[cur] = true;
    dep[cur] = dep[fath] + 1; // 每个点的深度等于父节点的深度 + 1
    for (int eg = head[cur]; eg != 0; eg = edges[eg].next) // 遍历子节点
        dfs(edges[eg].to, cur);
}

现在A点的深度比B点深，所以我们先让B点往上“爬”，爬到与A点深度相等为止。然后A点和B点再一起往上爬，直到两点相遇，那一点即为LCA：

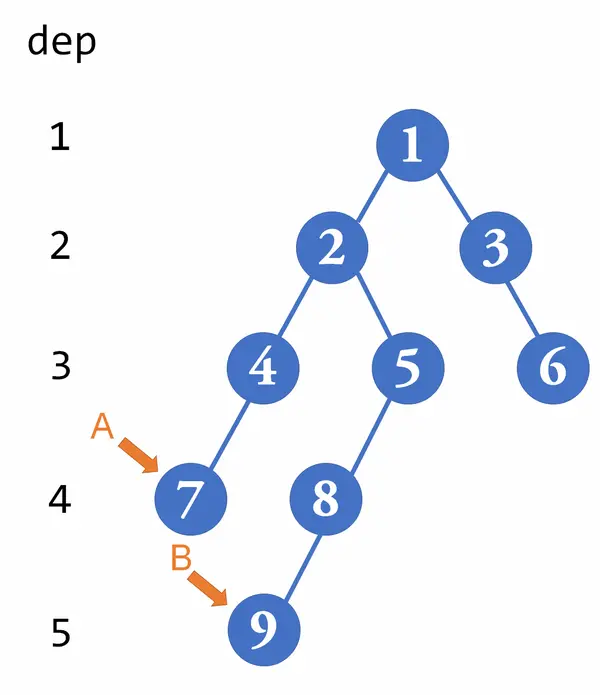
由此容易发现，每次查询LCA的最坏时间复杂度是 O(N) 的。

有时候，我们需要进行很多次查询，这时朴素的复杂度就不够用了。我们考虑倍增算法来优化 it。

倍增优化LCA

倍增是在朴素算法上的一个优化，朴素算法就是两个点一步一步跳，而倍增是利用二进制性质大步大步跳。

倍增：从字面的上意思看就是成倍的增长 ,这是指我们在进行递推时,如果状态空间很大,通常的线性递推无法满足时间和空间复杂度的要求 ,就可以通过成倍的增长,只递推状态空间中在2的整数次幂位置上的值作为代表。

$首先要dfs获取a, b节点的深度,记录为dep[a],dep[b];$

$不妨让a在b的下方,即dep[a] > dep[b]。$

于是，求LCA的方式为:

1. 先让更深的a向上爬,直到和b深度一致。
2. 再a和b一起向上爬，二者一定会在某个祖先节点上首次相遇,即为LCA。

But ！

如果是逐层的往上爬,和后序递归求LCA复杂度一样,都是O(N),后序递归其实是逐节点向下的.

一种改进的上爬策略是:

$$不是一步步向上爬，而是2^j步向上跳跃,因此必要记录深度信息和祖先信息。$$

倍增预处理

对于每个节点，计算它的2^i级祖先节点，其中i从0开始递增。这可以通过自底向上的动态规划来实现。

void dfs(int u , int pre) { // u表示当前节点，pre表示它的父亲节点
    dep[u] = dep[pre] + 1 ;
    fa[u][0] = pre;
    for(int i = 1 ; (1 << i) <= dep[u] ; i++) { 
        fa[u][i] = fa[fa[u][i - 1]][i - 1]; // 核心DP转移
        //意思是now的2^i祖先等于now的2^(i-1)祖先的2^(i-1)祖先
        //2^i = 2^(i-1) + 2^(i-1)
    }
    for(int i = h[u] ; ~i ; i = ne[i]){ // 遍历子节点
        int j = e[i] ;
        if(j == pre) continue;
        dfs(j , u);
    }
}

这样，往上爬的次数可以被大大缩短（现在变成“跳”了）。

例如，a和b本来相差22的深度，现在b不用往上爬22次，只需要依次跳16、4、2个单位，3次便能达到与a相同的距离。

LCA过程

预处理完毕后，我们就可以去找它的LCA了，为了让它跑得快一些，我们可以加一个常数优化 (From 洛谷) orz

for(int i = 1; i <= n; ++i) //预先算出log_2(i)+1的值，用的时候直接调用就可以了
      lg[i] = lg[i-1] + (1 << lg[i-1] == i);  //看不懂的可以手推一下

接下来可以LCA了。

首先使两点深度相等, 两者深度相等后，如果两个点已经相遇，那么问题就得以解决。
如果尚未相遇，我们再让它们一起往上跳。问题在于，如何确定每次要跳多少？正面解决也许不太容易，我们逆向思考：如何在a、b不相遇的情况下跳到尽可能高的位置？如果找到了这个位置，它的父亲就是LCA了！ヾ(^▽^ヾ)

送上LCA板子：

int LCA(int x, int y) 
{
    if(depth[x] < depth[y]) //用数学语言来说就是：不妨设x的深度 >= y的深度
        swap(x, y);

    while(depth[x] > depth[y])
        x = fa[x][lg[depth[x]-depth[y]] - 1]; //先跳到同一深度

    if(x == y)  //如果x是y的祖先，那他们的LCA肯定就是x了
        return x;

    for(int k = lg[depth[x]] - 1; k >= 0; --k) //不断向上跳

        if(fa[x][k] != fa[y][k])  //因为我们要跳到它们LCA的下面一层，所以它们肯定不相等，如果不相等就跳过去。
            x = fa[x][k], y = fa[y][k];

    return fa[x][0];  //返回父节点
}