前言

这是很久以前写的东西了。
完整版的笔记在这里。

一、如何表示多项式

现在给你一个问题：给定两个多项式，计算二者的乘积。（多项式乘法）
非常简单啊，我们直接采用乘法分配律秒了这题，时间复杂度是 $O(nm)$。（即高精度乘法）

我们想学会多项式乘法，当然要先知道如何存储多项式。很显然地，我们可以用数组存储多项式每一项系数。
如 $A(x)=x^2 + 3x + 2 \rightarrow A = [2,3,1]$。这种存储方式的优点在于，数组第 $k$ 项即多项式的 $k$ 次方项的系数。这就是系数表示法。

众所周知，我们以最简单的多项式 $y=kx+b$ 为例，发现它可以对应到平面直角坐标系中的唯一一条直线。所以我们只要知道 $k$ 和 $b$ 就能知道这个多项式。
回到了起点，还是要求出多项式每一项的系数。
但由于两点确定一条直线，我们只要知道直线上的 $(x_1,y_1)$ 和 $(x_2,y_2)$ 两点，就可以求出这条直线（代入后联立得二元一次方程组）。

事实上，任意一个 $d$ 次多项式都可以由平面直角坐标系中的 $d+1$ 个点唯一确定，这就是点值表示法。
这么说好像仍然不是很好理解，我们把这 $d+1$ 个点代入到原来这个多项式中：
$\{ (x_0,P(x_0)),(x_1,P(x_1)),\dots,(x_d,P(x_d)) \}$
$P(x)=p_0 + p_1x + p_2x^2 + p_3x^3 + \dots + p_dx^d$

我们把这 $d+1$ 个点代入多项式，得到了 $d+1$ 个 $d$ 元方程，于是就可以解出各个系数了！！

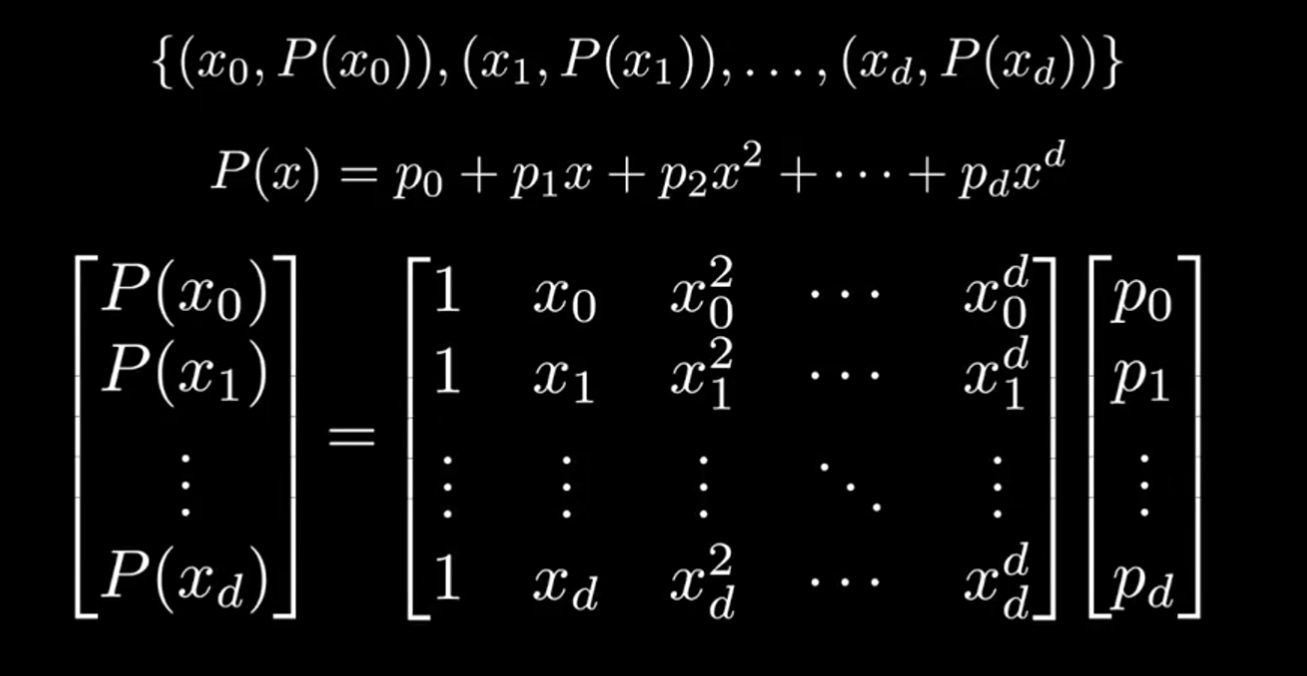
二、点值表示法的优点与缺点

那么回到原题，假设两个多项式都是 $n$ 次的，则它们的乘积就是 $2n$ 次的，需要用 $2n+1$ 个点来表示。
那么我们只要挑这两个多项式图像上的 $2n+1$ 个点，算出它们的值，并且把 $x$ 相同的两个点的 $y$ 值相乘，就能得到答案！
这似乎是 $O(N)$ 的复杂度！
但分析一下：先选取 $2n+1$ 个点，对每个点需要 $O(n)$ 计算它的值，于是乎瓶颈成为了预处理——这仍然是 $O(N^2)$ 的复杂度……

三、系数表示法到点值表示法的快速转换

于是问题就转化为，如何快速计算每个多项式的值？即如何把系数表示法与点值表示法快速转换？
FFT 横空出世！

先考虑这个问题：给定一个 $d$ 次多项式 $P$ 和 $n$，你需要选 $n$ 个 $x_1,x_2,\dots,x_n$，计算 $P(x_1),P(x_2),\dots,P(x_n)$，其中 $n \geq d+1$。
最暴力的做法当然是求出每个点的值，然后 $O(nd) \geq O(n^2)$，回到起点。

我们来整点更快的！给定一个函数 $y=x^2$，它大概长成 “U” 的形状。那么我们会发现，只要求出 $(x,y)$，就能知道 $(-x,y)$，其原因是因为这是一个偶函数，即 $f(x)=f(-x)$。
同样的，对于 $y=x^3$，只要求出 $(x,y)$，就能知道 $(-x,-y)$，它是一个奇函数，即 $f(x)=-f(-x)$。

于是，对于一个奇函数或偶函数，只要计算一半的点就好了，剩下的一半我们都可以通过奇偶性直接推出。

对于一个一般的多项式呢？我们可以把它分成奇函数和偶函数的和，把奇函数部分提出来一个 $x$，就可以得到两个偶多项式函数。

根据刚刚的分析，就有：
$P(x_i)=P_e(x_i^2)+x_i P_o(x_i^2)$
$P(-x_i)=P_e(x_i^2)-x_i P_o(x_i^2)$
二者只需计算一个就可得出另一个。

于是我们把一个多项式分解为奇偶两部分，每部分降到了 $\lceil \frac{n}{2} \rceil + 1$ 次。
对于两个新的函数，又是一个子问题，只不过要求最开始点的平方的函数值。由于最开始我们取了一对相反数 $x,-x$，平方后就只剩下 $\lceil \frac{n}{2} \rceil$ 个点了。子问题？？直接递归！！
我们只要递归求 $P_e(x)$ 和 $P_o(x)$，即可合并到 $P(x)$ 原问题！
分析一下复杂度，$T(n)=2T(\frac{n}{2}) +O(n)=O(n \log n)$！

然而你会发现，两个子问题代入的值都是平方形式的，它一定是非负，而我们解决该问题的基础是代入一对相反数！所以这个做法被否定了。

四、复数

$i=\sqrt{-1}$ 任意一个复数都可以被表示为 $a + bi$，$a$ 是实部， $b$ 是虚部。
任意一个复数都可以表示在复平面中，复数的模长就是其向量的长度，即 $\sqrt{a^2+b^2}$。
向量和 $x$ 轴的夹角被称作辐角。

所以我们需要选一些复数，让它们平方后仍然是正负成对出现（注意区分负和复）。
观察到这相当于是要求出 $1$ 的 $n$ 次方根！（我真的累了不想解释了，可以拉到底部看视频解释）
则任意相邻两点的夹角为 $\frac{2 \pi}{n}$。

五、停更

由于 NOIP 训练、五十连测，停更。

Upd On 2025.05.23：开！