上一节介绍了组合数Cmn的计算公式和从公式入手的直接计算方法,本节将介绍关于组合数的两个重要定理。第一个定理来源于二项式x+1的指数展开以及杨辉三角,它的表达式为Cmn=Cm−1n−1+Cmn−1。本节首先介绍,杨辉三角是什么,以及它如何与组合数互相联系起来。
杨辉三角的历史渊源可以自己去了解,不属于本帖的重点讨论内容,下图中的三角形数表就是杨辉三角的一部分。
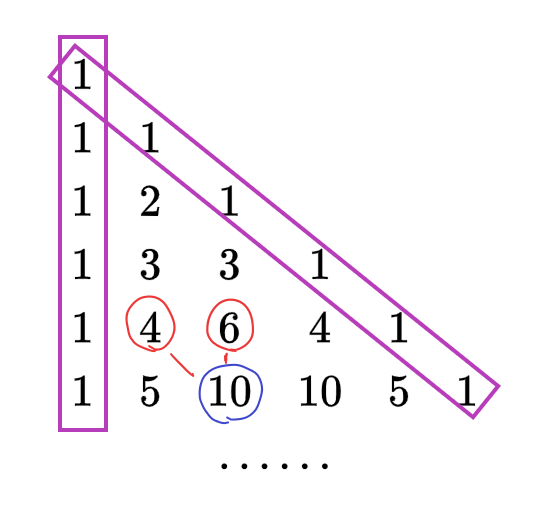
从中可以得出以下结论:
1. 每一行的第一个和最后一个都是1(如紫色方框所示)
2. 每一个数都由其正上方和左上方的数累加而得(如蓝色圈中的10,是由上一行红色圈中的4和6累加得到)
而结合(x+1)n的展开式C0n∗x0+C1n∗x1+…+Cn−1n∗xn−1+Cnn∗xn即∏ni=0Cin∗xi,将组合数公式代入计算后得知,其中每一行的n个数,都和C0n,C1n,…,Cnn一一对应,可以利用这样的对应关系,通过构造杨辉三角来求得某一确定的Cmn
size_t combine(size_t n, size_t m, size_t p) {
if (n < 2) return 1;
vector<vector<size_t>> cb = { //先把三角形顶部构造好
{1}, {1, 1}
};
for (int i = 2; i <= n; i++) { //然后按照上述定理构造完n层
cb.push_back(vector<size_t>(i + 1, 1)); //两端一定是1
for (int j = 1; j < i; j++) { //除了两端之外,其余部分都要累加
cb[i][j] = (cb[i - 1][j] + cb[i - 1][j - 1]) % p;
}
}
return cb[n][m];
}
第二个定理也许只有数学系的才会知道,不过本帖可将其作为补充。如果将组合数计算函数combine的参数m,n,p利用起来,将m,n转换成为p进制下的¯a0a1a2…an和¯b0b1b2…bn(其中ai,bi是转换后各数位上的数码,那么Cmn%p=(∏ni=0Caibi)%p。考虑到an,bn分别相当于m%p,n%p,而¯a0a1a2…an−1和¯b0b1b2…bn−1分别相当于m/p,n/p,该定理又可以写成同余方程式Cmn≡Cm/pn/p∗Cm%pn%p(mod p)。此即Lucas定理,比之前的所有方法都省时间。
证明如下:
1. 令m=x1∗p+y1,n=x2∗p+y2,则等式右侧可转化为Cx1x2∗Cy1y2;
2. Cmn是(x+1)n的展开式中xm项的系数,用x1∗p+y1替换m,就转化为了xx1∗p∗xy1;用x2∗p+y2替换n,可以得到(x+1)x2∗p+y2,即((x+1)p)x2∗(x+1)y2,模p的情况下,可以替换成(xp+1)x2∗(x+1)y2;
3. 由最初的代换可得y1=m%p,y2=n%p,必然小于p,而xp+1的幂次展开式中,除了常数项外,包含x的幂次必然是p的倍数,不可能小于p,因此xy1项必然由(x+1)y2提供,xx1∗p项必然由(xp+1)x2提供;
4. xx1∗p项的系数为Cx1x2,xy1项的系数为Cy1y2,相乘即为Cx1x2∗Cy1y2,它等同于Cmn;
5. Cmn≡Cm/pn/p∗Cm%pn%p(mod p)得证,则Cmn%p=(∏ni=0Caibi)%p也一定是正确的
该部分的函数用lucas命名,以区别于前面的combine,在计算过程中,前面的combine需要重复利用。函数lucas有迭代和递归两种写法,迭代法用到了Cmn%p=(∏ni=0Caibi)%p,而递归法用到了Cmn≡Cm/pn/p∗Cm%pn%p(mod p)
迭代:
size_t lucas(size_t n, size_t m, size_t p) {
size_t ans = 1;
while (n > 0 && m > 0) { //取到0那就是1
size_t a = m % p, b = n % p; //依次取一位
m /= p;
n /= p;
ans = (ans * combine(b, a, p)) % p; //按累乘式计算
}
return ans;
}
递归:
size_t lucas(size_t n, size_t m, size_t p) {
if (m == 0) return 1;
//取模部分的组合数用combine算出来,除法部分的组合数继续递归调用lucas
return lucas(n / p, m / p, p) * combine(n % p, m % p, p);
}

