质数的定义都知道吧（小学三四年级就学过）不知道也没关系，质数的定义就是说，在大于 $1$ 的整数中，如果这个数只包含 $1$ 和它本身两个因数，这个数就叫做质数（也叫素数）。

第一个知识点：质数的判定——试除法

这个非常简单，估计很多人都学过，首先，先从定义开始暴力写代码。

bool is_prime(int n){
    if (n <= 1) return false;
    for (int i = 2; i < n; i++){
        if (n % i == 0)
            return false;
    }
    return true;
}

这个算法时间复杂度明显是 $O(n)$ 的，很慢，所以我们要优化。
对于一个数 $n$，如果能被 $x$ 整除，那么他一定也能被 $n \div x$ 整除，所以我们模拟到 $\sqrt n$ 就行了。

bool is_prime(int n){
    if (n <= 1) return false;
    for (int i = 2; i <= n / i; i++){ // 用 i * i <= n 或 i <= sqrt(n) 也行，不过前者怕溢出（倒也没啥，开long long就行了），后者怕超时（前面先设一个变量就行了）
        if (n % i == 0)
            return false;
    }
    return true;
}

第二个知识点：分解质因数——也是试除法

这个也是很简单，三四年级都学过分解质因数，用的是短除法，比如 $180$。

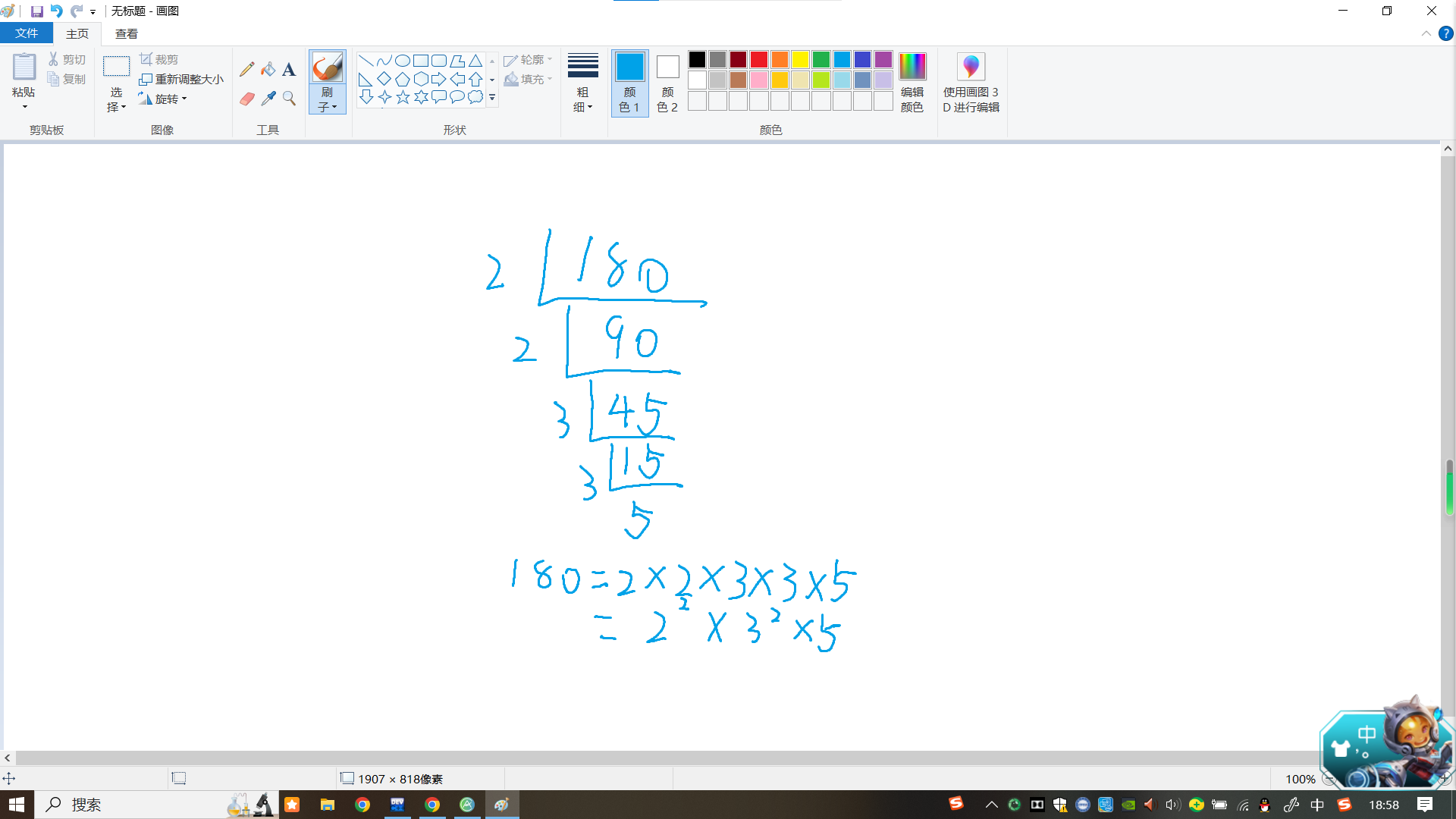
照着这个模拟就行了。

void divide(int n){
    for (int i = 2; i <= n / i; i++){
        if (n % i == 0){
            int ans = 0;
            while (n % i == 0){
                n /= i;
                ans++;
            }
            printf("%lld %lld\n", i, ans);
        }
    }
    if (n != 1) printf("%lld 1", n);
}

时间复杂度明显也是 $\sqrt n$，但他的实际复杂度是小于 $\sqrt n$ 的。

第三个知识点：质数筛——埃氏筛、线性筛

质数筛的意思就是从 $1 \sim n$ 中把所有的质数挑出来，最简单的方法就是从 $1 \sim n$ 遍历一遍依次判断是不是质数，当然，时间复杂度很慢，所以我们要用筛法。

埃氏筛

从 $2$ 开始如果遇到质数，就把它放到数组内，顺便把它的倍数全部标为不是质数。

void get_primes(){
    for (int i = 2; i <= n; i++){
        if (!st[i]){ // st[i] = true，说明i不是质数
            primes[++cnt] = i;
            for (int j = i + i; j <= n; j += i) st[j] = true;
        }
    }
}

这样，$primes$ 数组里存的是 $1 \sim n$ 里所有的质数，$cnt$ 是 $1 \sim n$ 中质数的数量。
通过推一些式子后，可以发现时间复杂度大约是 $O(n \log\log n)$，跟线性时间复杂度差不多了，完全可以接受。
虽然这个不是埃及人发明的，但他是一个叫做埃拉托斯特尼（他是希腊人）的人发明的，所以叫做埃氏筛法。

线性筛

可以发现，埃氏筛筛得过程中，有些数可能会被重复筛多次，于是线性筛的思路就是，每一个合数只用它的最小因子筛掉。
先看代码：

void get_primes(){
    for (int i = 2; i <= n; i++){
        if (!st[i]) primes[++cnt] = i;
        for (int j = 1; primes[j] <= n / i; j++){
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

思路就是上面的那些，然后来证明一下正确性。
首先，$primes$数组里的质数是从小到大排列的，所以在第 $6$ 行的 break 没发生之前，$primes[j]$ 始终是小于等于 $i$ 的最小质因子的，那么 $primes[j]$ 绝对是 $primes[j] * i$ 的最小质因数。
所有的合数，肯定都会有最小质因数，所以肯定会被筛掉，而肯定只有一个最小的，所以只会被筛一次，这就是这个算法的原理。