Dijkstra算法

Dijkstra算法用于单源最短路问题，且用于的情况是边权值都是正数的情况下，常见的问题为从1号节点到n号节点的最短距离， Dijkstra算法又分为朴素Dijkstra算法和堆优化版的Dijkstra算法 。

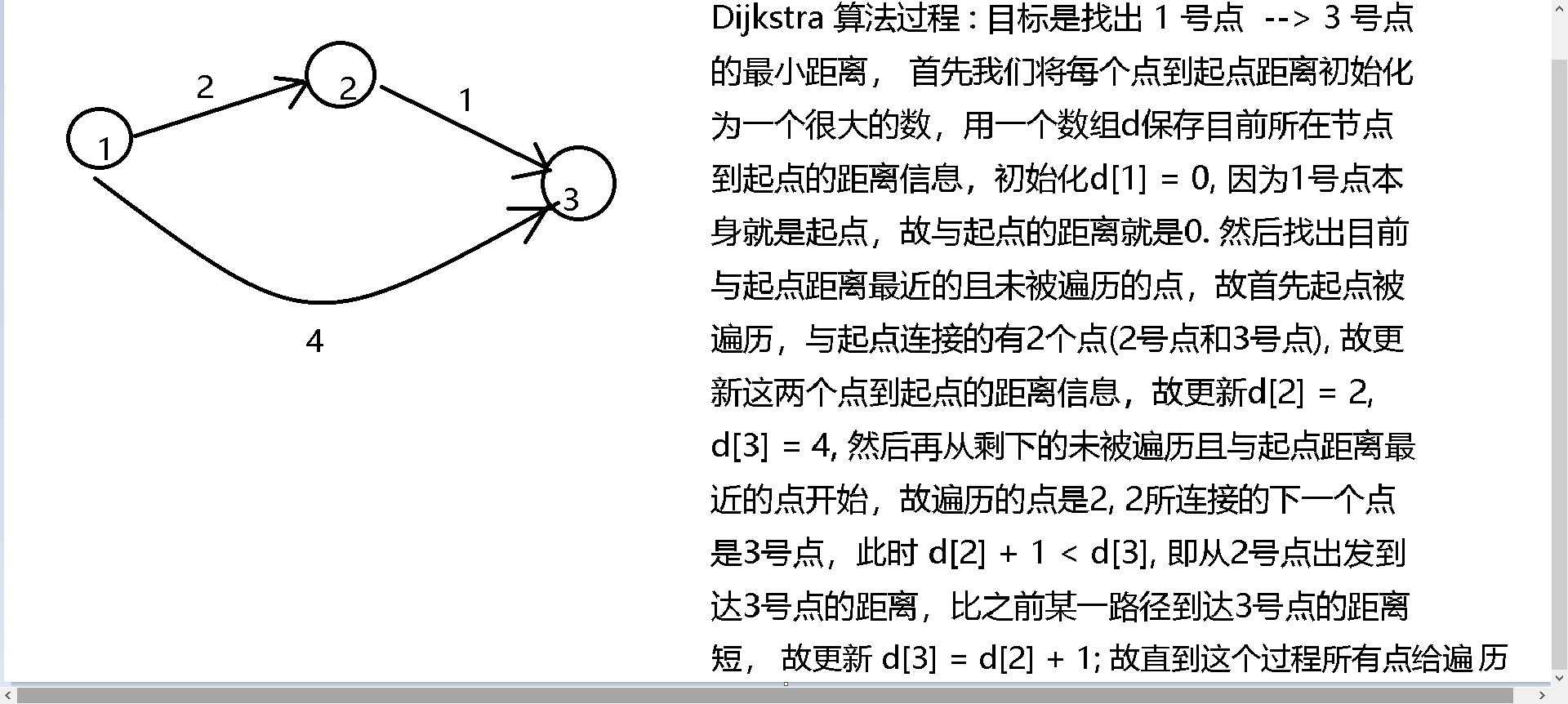
Dijkstra算法大致思路：主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止.故首先从未遍历的点中找出一个距离起点最近的一个点， 然后比较从目前遍历的点到其下个点的距离 + 自身到起点的距离 与 下一个点目前到起点的距离决定是否更新, 由于其每次是从当前距离起点最近的点到其连接下一个点的距离来判断是否进行距离的更新，因为每次拿来更新的点都是先找出当前未遍历的点中距离起点最近的那个点，故用这个点更新其连接的下一个点到起点的距离，若满足更新条件那么被更新的点是目前遍历情况下该点的距离起点一定是最小的，故当遍历完所有的点后，即可以在d[n]得到正确的答案， 具体见下图.

1.朴素Dijkstra算法实现 时间复杂度 O($n^2$)
练习的链接 : Dijkstra求最短路 I

#include<iostream>
#include<cstring>
using namespace std;

constexpr int N = 510;
constexpr int INF = 0x3f3f3f3f;

int n, m, g[N][N], d[N];    // 通过题目信息判断, 此时 n 最多为500, 而m最多为10^5.属于稠密图, 故这里用邻接矩阵存储比较好。
bool st[N];   // 保存某个节点是否被遍历过

auto dijkstra()
{
    d[1] = 0;           // 更新第一个点到起点的距离为0

    for(int i = 1; i <= n; ++i)       // 遍历所有节点    
    {
        int t = -1;
        for(int j = 1; j <= n; ++j)     // 找出目前剩余未被遍历节点中距离起点最小的节点
            if(!st[j] && (t == -1 || d[t] > d[j])) t = j;

        st[t] = true;            // 将该节点更新为已遍历状态

        for(int k = 1; k <= n; ++k)     // 更新距离 
            d[k] = min(d[k], d[t] + g[t][k]);
    }

    // 时间复杂度分析， 首先上面的大for循环为n , 然后里面看成2n, 故时间复杂度就是n2

    if(d[n] == INF) cout << -1 << endl;   // 若d[n] 未被更新则说明不存在到n号节点的路径
    else cout << d[n] << endl;
}

auto main() -> int
{
    memset(g, 0x3f, sizeof g);    // g邻接矩阵保存的信息为两条边之间的距离，初始化为一个很大的数
    memset(d, 0x3f, sizeof d);    // 同样初始化每个节点到起点1号节点的距离为一个很大的数
    cin >> n >> m;

    while(m--)      // 执行m次操作
    {
        int a, b, c; cin >> a >> b >> c;
        g[a][b] = min(g[a][b], c);      // 此时如果有多条重边，只保留一条最短距离的边
    }

    dijkstra();

    return 0;
}

2.堆优化的Dijkstra算法实现 O($mlogn$)

优化的思路，首先我们从上面的朴素做法可以看出，我们在找其中未被遍历且距离起点最短的点时间复杂度我们看为On, 故这里可以进行优化，使用小顶堆来保持，故此时找出距离最小的点的时间复杂度为O(1);然后对这个点的每一条边进行遍历，然后判断是否更新，若需要更新，则插入，堆的数据结构插入的时间复杂度为O($logn$); 故整个过程最坏的复杂度就是$mlogn$; 但我们这里实现一般都是使用C++里的优先队列，故每次插入一个数而不是修改某个数，故造成堆里面最坏有m个数字，故最坏的时间复杂度为 $mlogm$

练习链接: Dijkstra求最短路 II

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
using T = pair<int,int>;

constexpr int N = 1e+6, INF = 0x3f3f3f3f;
int n, m, e[N],w[N], ne[N], d[N], g[N], idx;    // n, m 都是 $10^5$级别的, 故这里看作稀疏图，采用邻接表来存储整个图
bool st[N];

auto add(int a, int b, int c)   // 邻接表来存储图需要进行插入操作，这里用w数组保存每一条边的权值
{
    e[idx] = b;
    ne[idx] = g[a], w[idx] = c, g[a] = idx++;
}

auto dijkstra()
{
    priority_queue<T, vector<T>, greater<T> > q;    // 堆优化，采用优先队列，并以小顶堆的方式进行存储
    d[1] = 0;
    q.emplace(0, 1);
    while(q.size())
    {
        auto item = q.top(); q.pop();
        int dist = item.first;
        int node = item.second;
        if(st[node]) continue;
        st[node] = true;
        for(int i = g[node]; i != -1; i = ne[i])    // 判断与目前遍历点其连接的点是否需要更新
        {
            int t = e[i];
            if(d[t] > dist + w[i])
            {
                d[t] = dist + w[i];
                q.emplace(d[t], t);       // 更新完一个点则入堆，表示未被遍历且距离得到更新
            }
        }
    }

    if(d[n] == INF) cout << -1 << endl;
    else cout << d[n] << endl;
}

auto main() -> int
{
    memset(g, -1, sizeof g);
    memset(d, 0x3f, sizeof d);
    cin >> n >> m;
    while(m--)
    {
        int a, b, c; cin >> a >> b >>c;
        add(a,b,c);
    }
    dijkstra();
    return 0;
}

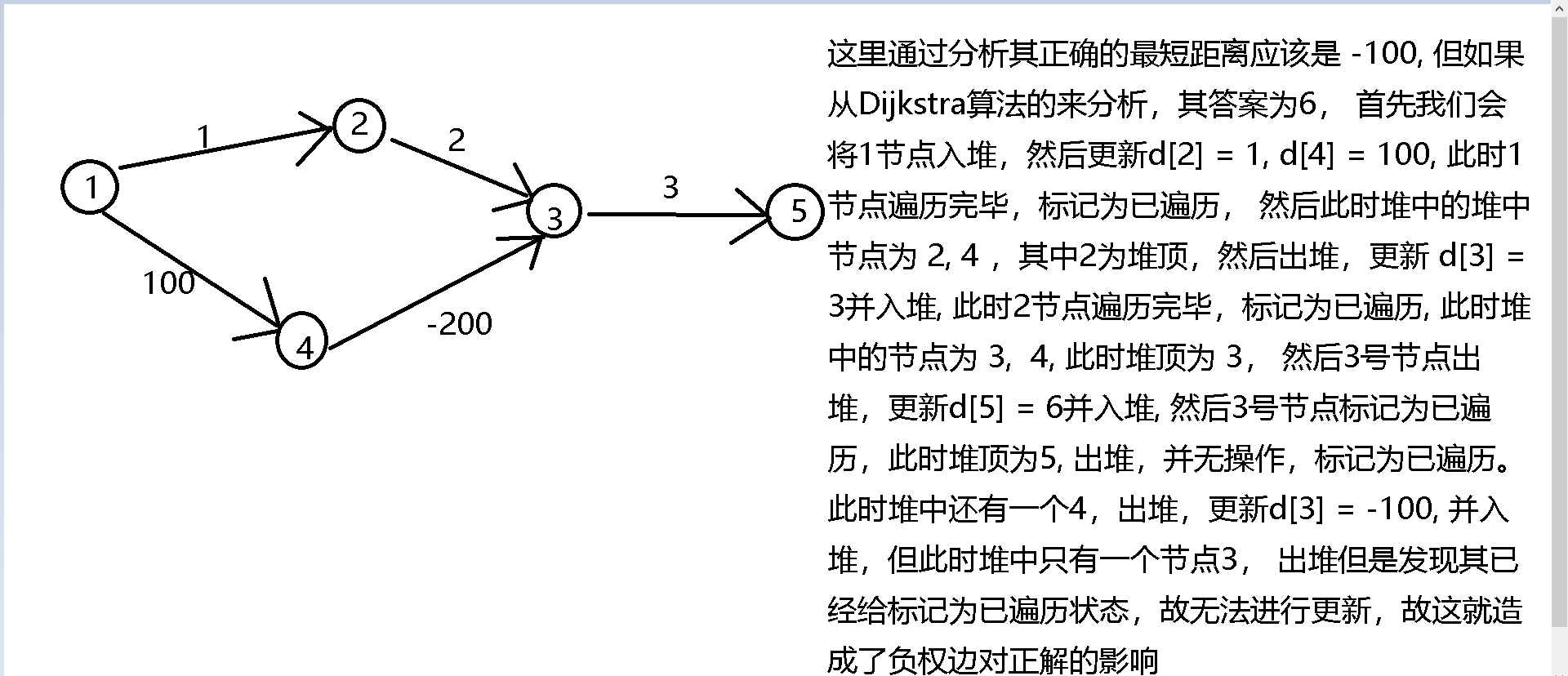
注意 : Dijkstra 算法不能用于负权边的情况

对于某些带负权边的情况，可能输出正确的结果，但某些情况是会输出错误的结果的,如下图的情况分析: