KMP算法
首先KMP模式匹配算法是针对朴素匹配算法的不足和低效提出的,要想真正理解KMP算法,我认为应该先理解朴素算法为什么低效
朴素算法的不足
来看下面这个例子 —> 摘自《大话数据结构》的一个例子
主串 S = “abcabcabc” , 要匹配的模式串 T = “abcabx”, 根据我们的朴素算法,其比较的过程如下:
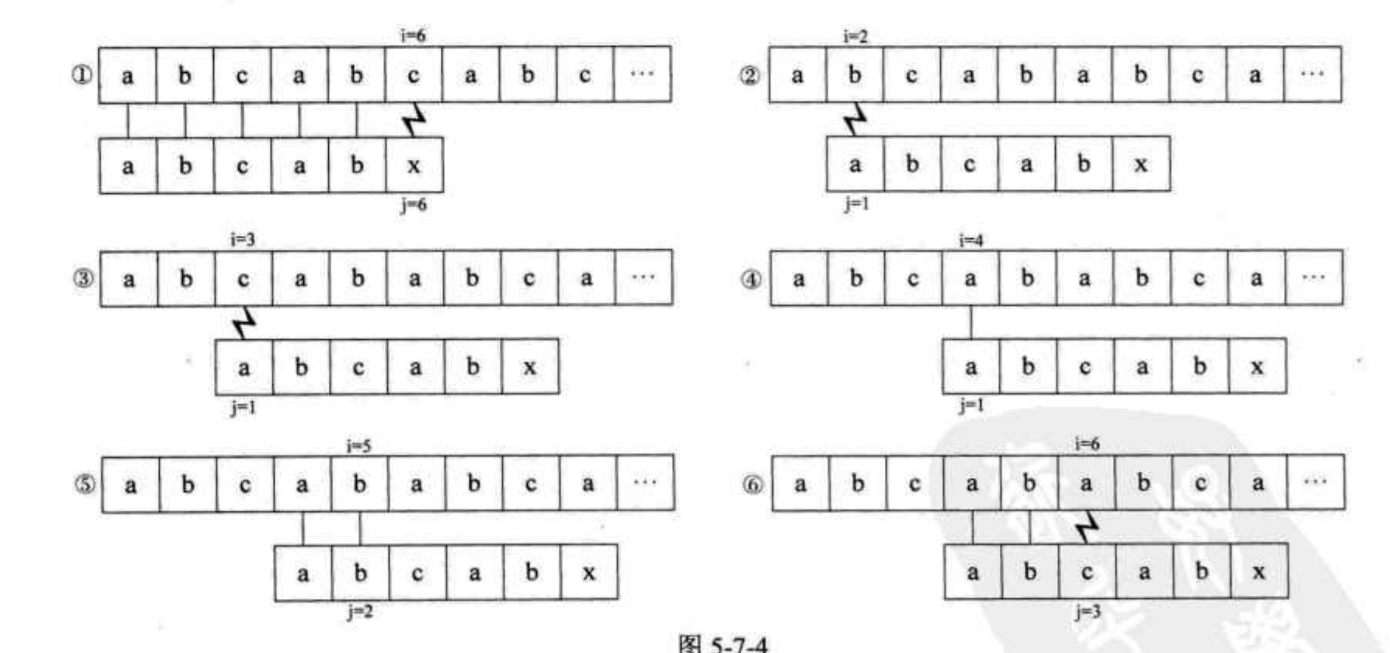
这里①中, 以主串的第一个字符作为起点与模式串进行匹配,当匹配到模式串第6个字符时二者不等,故重新回溯到主串的第二个字符作为起点开始匹配 (②的匹配情况), 故朴素算法的过程就是①②③④⑤⑥⑦⑧⑨这种的比较过程,我们来看看这个算法有那些冗余的操作,我们观察我们的模式串可以发现,abcabx种, 第1,2 个字符和第4,5个字符是相同的,即我们在分析上面①这种情况时,此时T[6] != S[6];但这说明前面第1 ~ 5 个字符是匹配的, 此时我们又知道我们模式串中第1,2 个字符和第4,5个字符是相同的,故此时并不需要将我们的j从1开始,直接从j = 3, T[3]与此时的S[6]开始比较,因为T[1], T[2] 已经跟S[4],S[5]匹配上了。即上图中的②③④⑤⑥⑦⑧这几步并没有必要,属于冗余操作.故要想直接省去这些步骤,我们就需要事先知道当某个字符串不匹配后应该从那个位置开始比较,这里这个例子中,当模式串的第六个字符不匹配时,我们从模式串的第三个开始和目前不匹配的主串的那个字符比较,而不是模式串从第一个开始和主串又一次回溯。故我们这里就需要预处理一下我们的模式串,保存其中每一个字符发生不匹配后,j下标应该移动到值,故这就是我们见到的KMP的代码中的next数组,这个例子中我们的next[6] = 3; 故KMP的一个核心就是如何求解next数组。
next数组的求解
1.首先我们要明白next数组的含义, 这里说下我的理解,我的理解是next数组以其下标表示模式串中的第几个字符,其所存储的内容为当这个位置的字符不匹配时,此时应该从模式串的第几个位置继续比较判断,当然若目前比较的字符前面的都没有相同的前缀和后缀,那只能从模式串的第一个位置继续比较,故KMP算法的高效取决于要比较的模式串本身各个字串的相似程度。
//next数组求解的代码 其中 p数组为模式串字符数组,下标从1开始,长度为n. ne[1] = 0;
for(int i = 1, j = 0; i <= n;)
{
while (j && p[i] != p[j]) j = ne[j];
if (j == 0 || p[i] == p[j]) ++j, ++i, ne[i] = j;
// 若此时为j = 0,表示回溯到原点,没有相应的后缀和前缀匹配.故++j,表示1,即此时重新从第一个字符开始匹配
// 由于next[x] = k 表示的含义是当前第x个字符不匹配,第1 ~ 第k - 1 个字符和 第x - k + 1 ~ 第 x - 1 个字符相同
//故这里if如果是第二种情况为真,是先++i,++j,然后再next[i] = j;
}
// 注意这里代码的话其for循环的终止条件是 i <= n, 其实这里往前后多算了 next[n + 1] 的值
// 主要是针对多次匹配的问题做的考虑。因为如果在著主串中找到了第一个匹配的子串时,这时想
// 要继续求解的话,此时主串的位置下标是i, 即S[i] == T[j], 且j == n, 此时在主串S中完成了
// 第一条完整模式串的匹配,此时想继续匹配下一个同样通过next数组跳过一些相同的前缀和后缀的长度
KMP匹配过程
// 其中 m 为主串的长度,n为模式串的长度,下标从1开始,
for(int i = 1, j = 1; i <= m; ++i)
{
while (j && s[i] != p[j]) j = ne[j]; // 若不匹配直接j下标根据next数组跳到相应的位置
if (!j || s[i] == p[j]) j ++ ; // 若j为0,j = 1 或者此时两个字符相等 ++j;
if (j == n + 1) // 若 j == n + 1, 说明完成了n个字符的匹配,说明完成一次子串的匹配
{
j = ne[j]; // 若只需找到最前面的子串出现的位置则不需要这句,若要找多处则需要
// 匹配成功后的逻辑
}
}
例题练习 : 831. KMP字符串
#include<iostream>
using namespace std;
constexpr int N = 1e+6 + 10;
int n, m;
char p[N], s[N];
int ne[N];
auto main() -> int
{
cin >> n; cin >> p + 1;
cin >> m; cin >> s + 1;
for(int i = 1, j = 0; i <= n;)
{
while (j && p[i] != p[j]) j = ne[j];
if (j == 0 || p[i] == p[j]) ++j, ++i, ne[i] = j;
}
//匹配
for(int i = 1, j = 1; i <= m; ++i)
{
while (j && s[i] != p[j]) j = ne[j];
if (!j || s[i] == p[j]) j ++ ;
if (j == n + 1)
{
cout << i - n << " ";
j = ne[j];
}
}
cout << endl;
return 0;
}

