位运算更新中

位运算技巧：
(1) 获取二进制最低位的1：x & -x;
(2) 将二进制中最低位的1设置为0：x &= (x - 1); 或 x ^= x & -x;
(3) 求x的第k位数字：n >> k & 1; 或 1 << k & n;

• 1、为什么一个整数的负数是补码？
• 2、$lowbit(x)$
• 3、 快速幂求 $a^{b} \bmod p$
• 4、树状数组

1、为什么一个整数的负数是补码？

1.1 原码、反码、补码

举例：比如十进制数 $10$，其二进制数为 $1010$

原码：0...01010
反码：1...10101
补码：1...10110 （补码为反码加1）

int $32$ 位：

$1$：0000000000...01

$2$：0000000000...10

$3$：0000000000...11

1.2 补码如何计算

1 + x = 00000000000000000000000000000000
1 + 1111111111...1111 = 0000000000...00
2 + 1111111111...1110 = 0000000000...00
x +          ?        = 0000000000...00

$\color{#0000FF}{? = \sim x + 1}$

比如：

• $2$ 的补码，是将 $2$ 的二进制数先取反得1111111111...01，再加1，得1111111111...10

• 验证 $2$ 加上 $2$ 的补码是不是等于零？是的。

  • $2$ 的原码：0000000000...10
  • $2$ 的补码：1111111111...10
  • 加起来得：0000000000...00

所以，一个整数的负数是补码。

例子：程序验证 $10$ 的补码，补码为 反码加$1$，即 $\sim x + 1$。

#include <iostream>

using namespace std;

int lowbit(int x)
{
    return x & -x;
}

int main()
{
    int n = 10;
    unsigned int x = -n;
    for (int i = 31; i >= 0; i--)  cout << (x >> i & 1);
    // Output: 10的补码为：11111111111111111111111111110110
    cout << endl;
    return 0;
}

2、$lowbit(x)$

2.1 $lowbit(x)$ 的作用

• $lowbit(x)$：非负整数 $n$ 在二进制表示下最低位 $1$ 及其后面的 $0$ 构成的数值

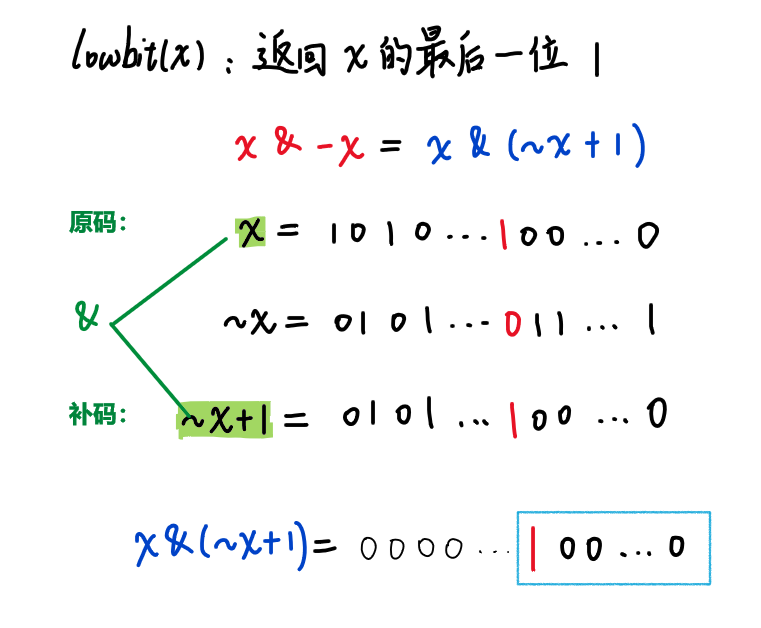
• $lowbit(x)$ 操作返回 $x$ 的最后一位 $1$

  • $x = {1010}_2$，那么 $lowbit(x)$ 返回 ${10}_2$，即 $lowbit(x) = 10$

  • $x = {101000}_2$，那么 $lowbit(x)$ 返回 ${1000}_2$，即 $lowbit(x) = 1000$

• 第一步：先把第 $k$ 位移到最后一位：$n$ 右移 $k$ 位：$n \gg k$

• 第二步：看个位是几？$x \And 1$

• 所以最后写成：$\color{#FF0000}{n \gg k \And 1}$

例子：将 $10$ 的二进制数输出：得到 $1010$

#include <iostream>
#include <string.h>

using namespace std;

int main()
{
    int n = 10;

    for (int k = 3; k >= 0; k--)  cout << (n >> k & 1);

    return 0;
}
// Output: 1010

2.2 $lowbit(x)$ 的实现

• $lowbit(x)$ 实现的时候就是 $\color{#FF0000}{x \And-x}$

• 首先，一个整数的负数是（原数的）补码。补码是取反$+1$，即 $\color{#0000FF}{-x = \sim x + 1}$

• 所以，$\color{#0000FF}{x \And (\sim x + 1)}$ = $\color{#FF0000}{x \And-x}$

2.3 为什么 $lowbit(x)$ 可以得到 $x$ 的最后一位？

2.4 $lowbit$ 的应用：可以统计 $x$ 中 $1$ 的个数

思路：就是每一次把 $x$ 的最后一位 $1$ 减掉，即 $x - lowbit(x)$，只需要算下减多少次，减多少次就有多少个 $1$

题目：位运算 —— 模板题 AcWing 801. 二进制中1的个数

n >> k & 1;         //求x的第k位数字
lowbit(n) = n & -n; //返回x的最后一位1

int solve(uint32_t n) {
    int res = 0;
    while (n)  n -= n & -n, res++;
    return res;
}

2.5 $lowbit$ 的应用：求一个数是否是 $2$ 的幂 (力扣231题)

思路：如果 n <= 0 则显然是 $false$；否则，有如下两种做法（不限于这两种）：

• $lowbit$：判断 n & (-n) == n，取负运算时将 $n$ 的二进制位取反然后再加 $1$。lowbit 的作用是取出 $n$ 二进制中从低位数第一个 $1$ 的位置 $k$，并返回 $2^{k}$。判断 n & (-n) == n 成立即意味着 $n$ 二进制位中从低位数第一个 $1$ 的位置就是最高位，因为 $2$ 的整数幂，二进制形式是 $n = (100......0)_{2}$。

• 判断 n & (n - 1) == 0，若成立，则表示 $n$ 只有最高的二进制位是 $1$，后续的二进制位都是 $0$，符合 2 的幂次。考虑一个数字是不是 $2$ 的整数次方：如果一个数字 $n$ 是 $2$ 的整数次方，那么它的二进制一定是 0...010...0 这样的形式；考虑到 $n - 1$ 的二进制是 0...001...1，这两个数求按位与的结果一定是 $0$。因此如果 n & (n - 1) == 0，那么这个数是 $2$ 的次方。

2.6 如何枚举二进制中的下一个 1？

• 我们可以用 $b$ 和最低位的 $1$ 进行按位异或运算，就可以将其从 $b$ 中去除，这样就可以枚举下一个 $1$。

for (; 条件; b ^= b & -b) {
    //...;
}

• 同样地，我们也可以用 $b$ 和 $b−1$ 进行按位与运算达到相同的效果，读者可以自行尝试推导。

for (; 条件; b &= (b - 1)) {
    //...;
}

LeetCode 37 解数独
链接：https://leetcode-cn.com/problems/sudoku-solver/solution/jie-shu-du-by-leetcode-solution/

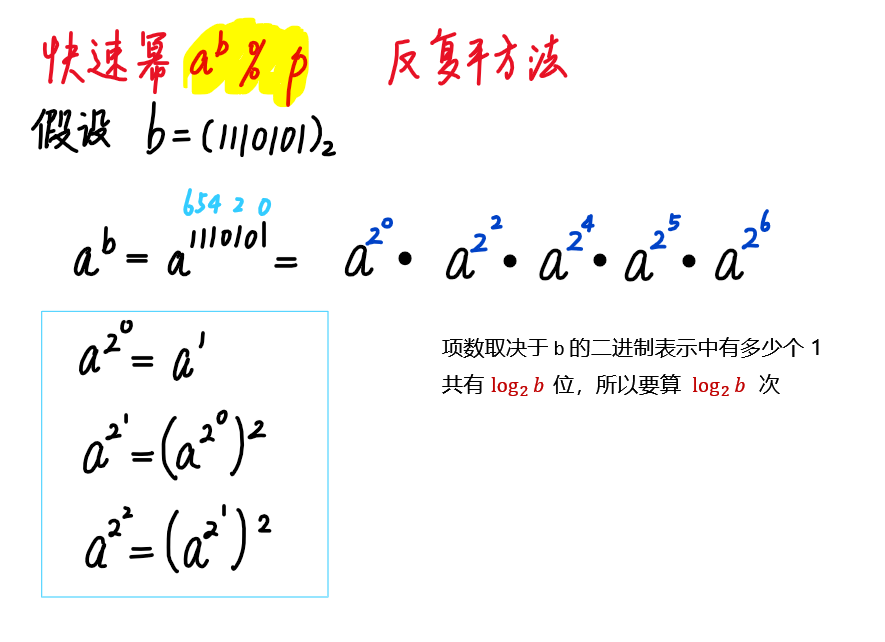
3、 快速幂求 $a^{b} \bmod p$

讲解：

例：$3 ^ 7 = ?$

$7 = 111_{2}$ (二进制)
$3 ^ 1 = 3$
$3 ^ 2 = 9$
$3 ^ 4 = 81$

这里 $3^1 * 3^2 * 3^4 = 3^7$

代码：

AcWing 89. a^b

#include <iostream>

using namespace std;

typedef long long LL;

int main()
{
    int a, b, p;
    cin >> a >> b >> p;

    // int res = 1; // 数据  123456789 0 1 会出错
    int res = 1 % p; //防止 b=0, p=1 的情况
    while (b) {
        //如果b的个位为1，b是奇数，那么拿一个a出来
        // 1ll是long long类型的整数1
        if (b & 1) res = (LL)res * a % p;
        a = (LL)a * a % p; //底数自乘
        b >>= 1; //再把个位去掉，即指数除2
    }
    cout << res << endl;

    return 0;
}

// 举例：(p随便取个模)
// 如果 b 是奇数，就取个 a 出来乘到 res 上，之后底数 a 自乘，指数 b 除 2（右移1位）
res  a  b  p    
1    3  7  1008
3    9  3
27   81 1
27 * 81 % 1008 = 171

4、 树状数组

优秀的树状数组学习笔记：https://www.acwing.com/file_system/file/content/whole/index/content/3084/

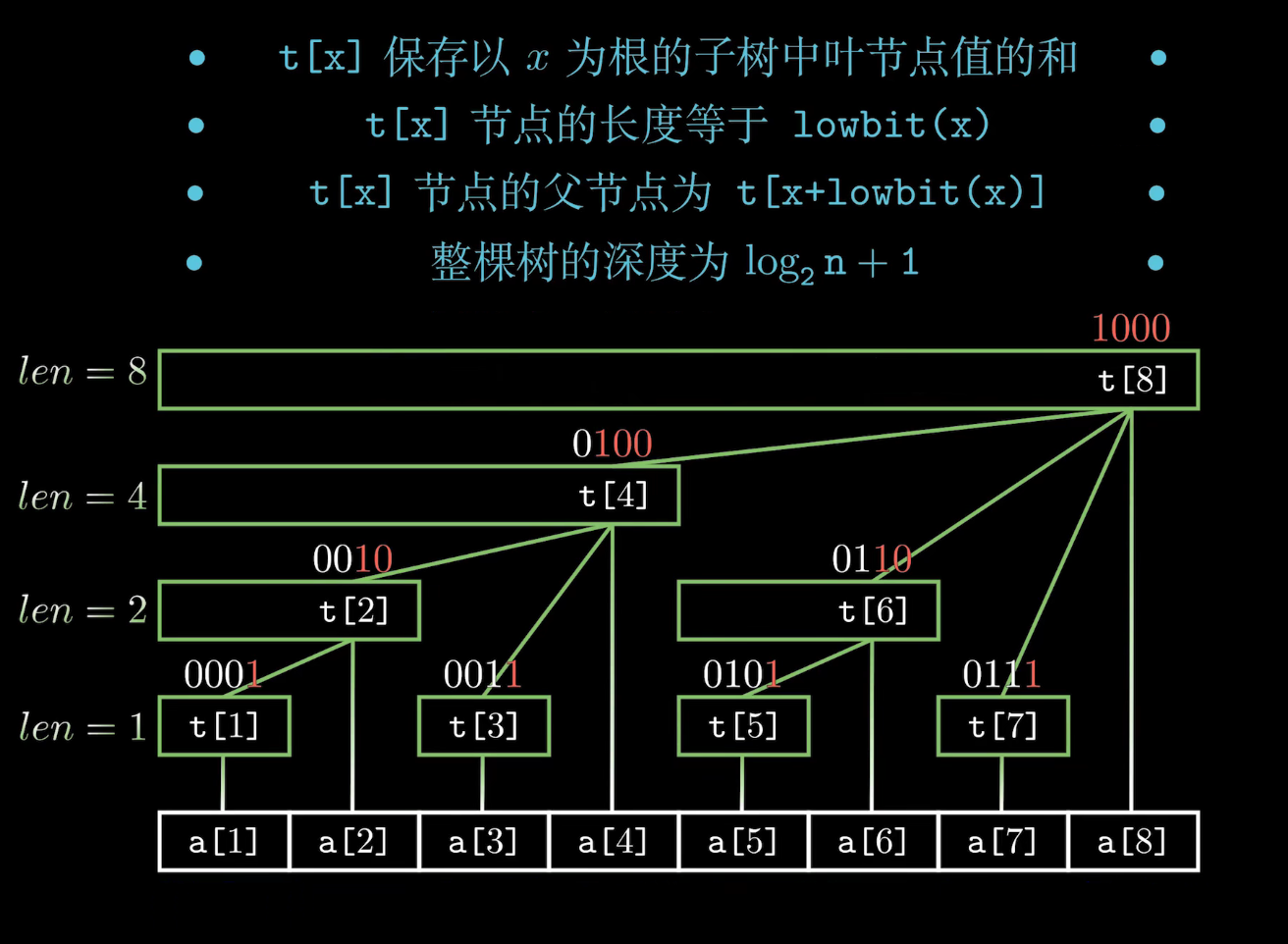
（图片来自B站视频：https://www.bilibili.com/video/BV1pE41197Qj ）

如何理解 $t[x]$ 节点的父节点为 $t[x+lowbit(x)]$？

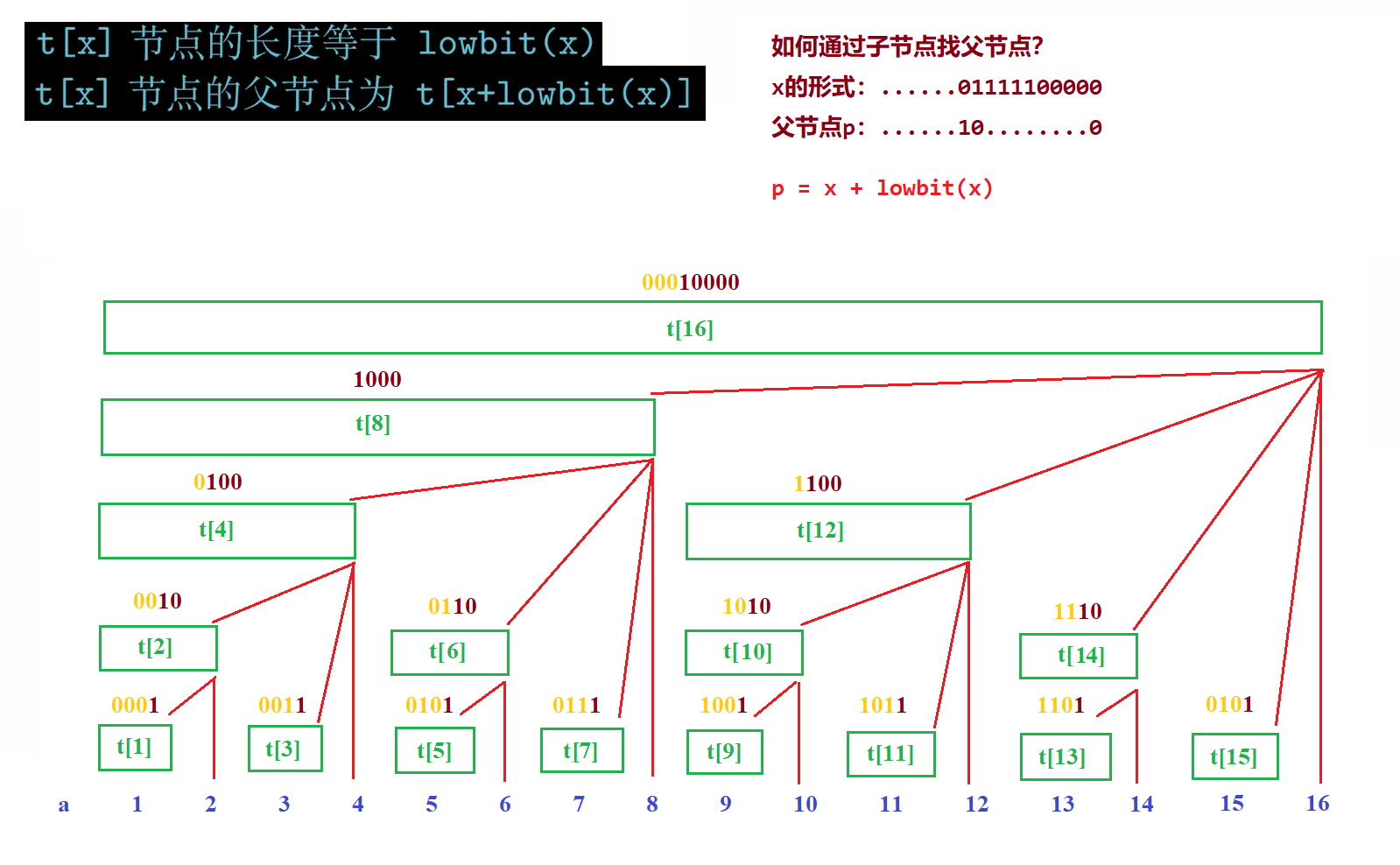
常用操作

$lowbit(x)$ : $x & -x$

① 求前缀和：

for (i = x; i; i -= lowbit(i))  res += tr[i];

② $a_{x} += v$

for (i = x; i ≤ n; i += lowbit(i))  tr[i] += v;

|--------------------|----------------|
                     x

x 往左是减- lowbit(x)，往右是加+ lowbit(x)。