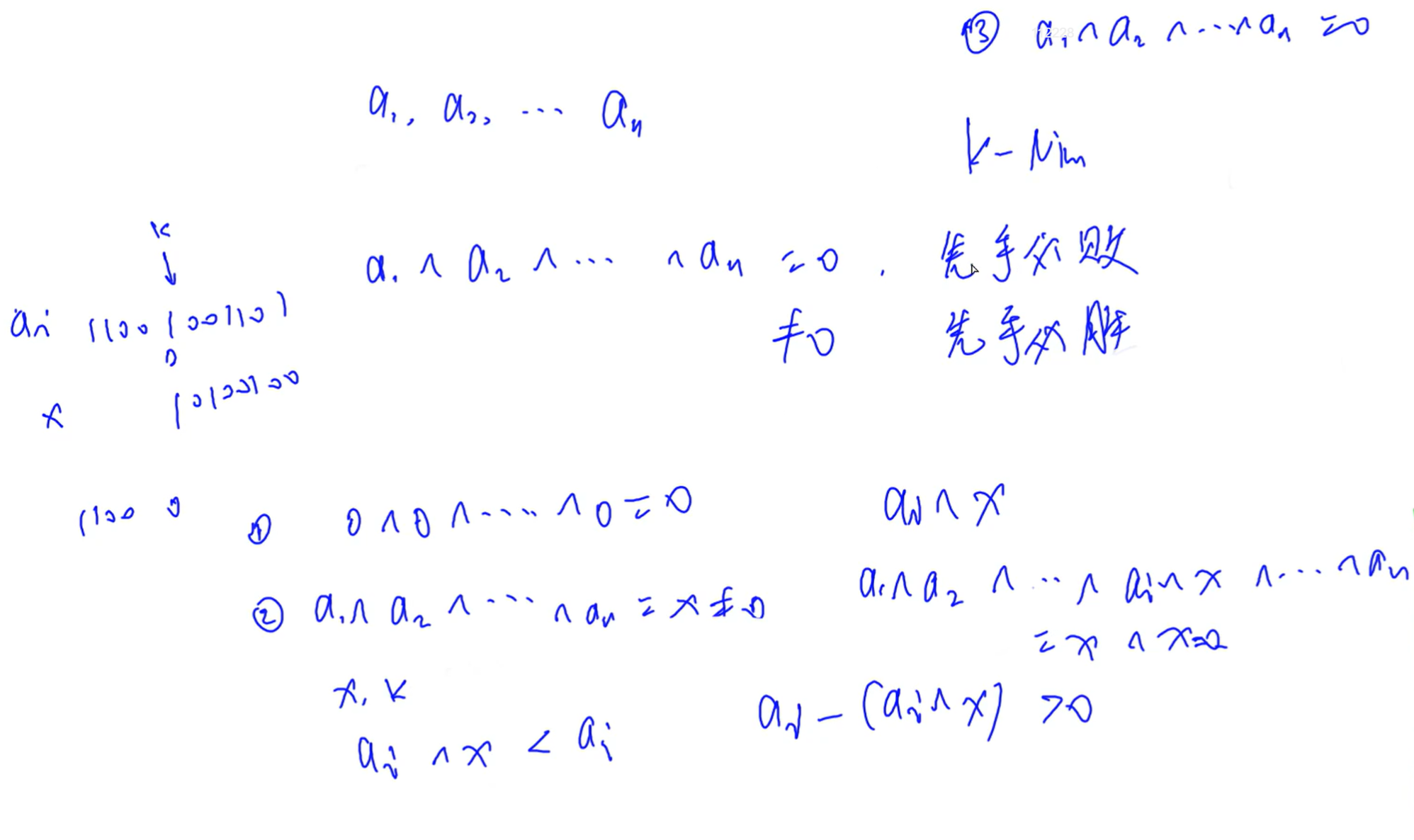$ 第一板块 $ $ 数学公式 $

目录

1.

组合数:$ C_n^m $ = $ n! \over (n-m)! \times m! $

排列数:$ A_n^m $ = $ n! \over (n-m)! $

2. 卡特兰数:$ Catalan_n $ = $ {1 \over n + 1} \times C_{2n}^n $(此公式用于求卡特兰数的第$n$项$C_n$)

3.完全平方数

# include <bits/stdc++.h>
# define sc scanf
# define pr printf
using namespace std;

typedef long long LL;

LL n;

int main(){
    sc("%lld", &n);

    LL s = sqrt(n);
    if(s * s == n){
        pr("1\n");
        return 0;
    }

    // 1 直接判定

    for(LL i = 1; i <= n / i; i ++){
        LL res = n - i * i;
        LL s = sqrt(res);
        if(s * s == res){
            pr("2\n");
            return 0;
        }
    }

    // 2 类似于勾股定理

    while(n % 4 == 0) n /= 4;

    if(n % 8 == 7){
        pr("4\n");
        return 0;
    } // 勒让德三平方和定理

    pr("3\n"); // 拉格朗日四平方和定理

    return 0;
}

4.博弈论:

1).891. Nim游戏

• 思路
• y总讲题

/*
重要结论：
先手必胜状态：可以走到某一个（于对手而言的）必败状态
先手必败状态：走不到任何一个（于对手而言的）必败状态
*/ 
# include <bits/stdc++.h>
# define sc scanf
# define pr printf
using namespace std;

int n, sum;

int main(){
    sc("%d", &n);

    for(int i = 1, x; i <= n; i ++){
        sc("%d", &x);
        sum ^= x;
    }

    if(!sum) pr("No");
    else pr("Yes");

    return 0;
}