一、定义

一个无向连通图中，

若删除一条边后，图分裂成两个不相连的子图，则该边为图的一条 割边 （或称 桥 ）；

若删除一个点及其相连的边后，图分裂成两个及以上不相连的子图，则该点为图的一个 割点 。

一般无向图（不一定连通）的割边和割点就是它各个连通快的割边和割点。

二、时间戳

1 - 定义

在图的深度遍历（ $DFS$ ） 过程中，

每个节点 $i$ 第一次被访问的时刻就是 $i$ 的时间戳 $dfn[i]$ 。

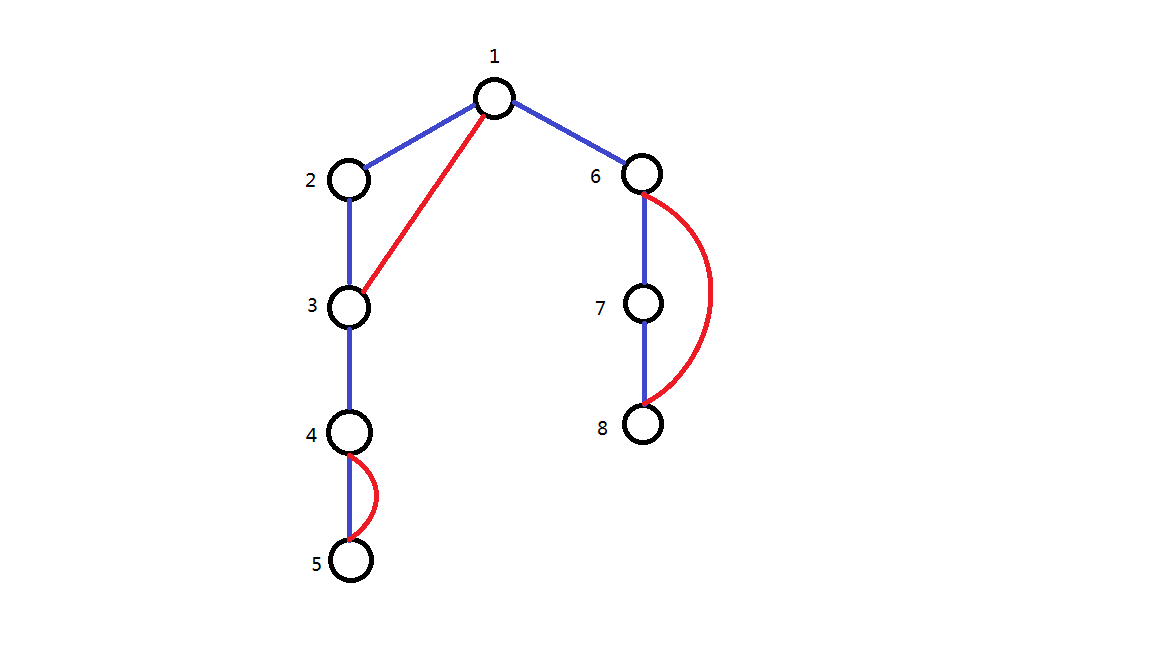
如图是 $dfn$ 示意图，

蓝色边是深度优先遍历时走过的边，我们称为 下降边 ；

红色边是未走过的边，我们称为 上升边 。

节点旁的数字为该节点的时间戳。

2 - 性质

$DFS$ 过程中，前 $t-1$ 个时刻已经完成，

目前下一个要访问的点是 $c$ ，那么 $dfn[c] = t$ ，

已知有两个已访问过的点 $a$ ， $b$ ， $dfn[a]<dfn[b]<t$ ，且 $(a,c)$ ， $(b,c)$ 都有边，

则 $DFS$ 时，会优先选择经过 $(b,c)$ 这条边访问 $c$ ，

即将 $(b,c)$ 作为下降边， $(c,a)$ 作为上升边。

从上图中 $6$ ， $7$ ， $8$ 号点的情况可以更直观地感受到。

证明：

因为 $DFS$ 的原则就是：能不回溯就不回溯，

既然从 $b$ 能直接到 $c$ ，就不用从 $b$ 回溯到 $a$ 再访问 $c$ 。

这就造成了一个重要的性质： 尽量把连接着上升边的点纳为儿子 ，

三、追溯值

1 - 定义

设 $subtree(x)$ 为以 $x$ 为根的子树，

节点 $i$ 的追溯值 $low[i]$ 为以下节点的时间戳最小值：

• 1. $subtree(i)$ 中的节点
• 1. 与 $i$ 之间用上升边连接的节点

2 - 性质

根据我们推出的时间戳的性质，

$i$ 会尽量把有上升边的点纳为儿子， $i$ 的儿子也会尽量把有上升边的点纳为自己的儿子。

以此类推， $i$ 想要上升，又不想逆着下降边走，

要么自己就连着上升边；要么就顺着下降边，找子树里的后代要。

这与 $low[i]$ 的定义不谋而合，

因此 $low[i]$ 就是 $i$ 不逆着下降边走，到达的最早的节点的时间戳 。

三、割边

在 $DFS$ 树中， $x$ 是 $y$ 的父亲，

若 $dfn[x]<low[y]$ ，则 $(x,y)$ 是割边。

很好理解，不允许 $y$ 逆着 $(x,y)$ 走和把 $(x,y)$ 删除是等效的，

$y$ 只能靠自己或者后代的上升边与时间戳小于等于 $dfn[x]$ 的点保持连通。

如果这都做不到（即 $low[y]>dfn[x]$ ），那么这棵以 $y$ 为根的子树就完全孤立了。

四、割点

在 $DFS$ 树中， $x$ 是 $y$ 的父亲，

若 $dfn[x]<=low[y]$ ，则 $x$ 是割点，

特别地，若 $x$ 是 $DFS$ 树的根节点，则它至少要有两个儿子，才能是割点。

证明与割边类似，不再赘述。