概述
我们在前面学习了最短路径与最小生成树的图论问题,所以我们今天来看一下二分图相关问题。当然这一部分还是算法基础课的图论简单知识点!大佬可以不用看 hh
我们来看一下这一次分享的目录::
- 二分图相关知识点
- 染色法判定二分图
- 匈牙利算法(匹配问题)
- 网络流问题(最大流与最小流)
这个知识点我会在图论四补充下面我们来看一下这一部分相关知识点!
什么是 二分图
二分图又称作二部图,是图论中的一种特殊模型。
官方定义:
设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。简而言之,就是顶点集V可分割为两个互不相交的子集,并且图中每条边依附的两个顶点都分属于这两个互不相交的子集,两个子集内的顶点不相邻。
二分图的一个等价定义是:不含有「含奇数条边的环」的图
通俗点讲:
就是将图中的节点分到两个集合中,满足:只存在由一个集合中的点指向另一个集合中的点的边。(也就是说两个集合中点不互通)
上面由于太过于官方,我们来这样理解!
论谈恋爱关系的二分图:
首先通过简单的例子来引入二分图的定义。假如我们有一群男生和女生,任意一对男女之间都可以建立暧昧关系。这样我们可以将所有男女作为分属两个集合中的点,一对男女分属两个集合,可以建立关系;但是两个在同一集合中的男生或者女生就不能建立关系,因为他们中没有搞基或者搞LES的。这样的一群男女以及他们的暧昧关系就构成一个二分图。也就是说,对于任意一个图G = (V, E),如果我们能够将它的点集V划分为这样的两个点集V1和V2,使得边集E中所有边的两端点一定分属两个点集,那么称这个图为二分图。
图论中,一个「匹配」(matching)是指一个边的集合,其中任意两条边都没有公共顶点。还是以上述例子来说明,同一个男生(或者女生)可以有多个暧昧对象,但是只能和一个异性建立恋爱关系。这样这群男女中所能够产生的恋爱关系,称为他们的一个“匹配”。所谓二分图的最大匹配,就是指边数最多的匹配,对应到上述例子中就是指所能够产生的最多对情侣。所以我们可以感受到,“匹配”这个翻译还是非常形象的,它就是指节点“一对一”的对应关系。
看个图:
二分图:
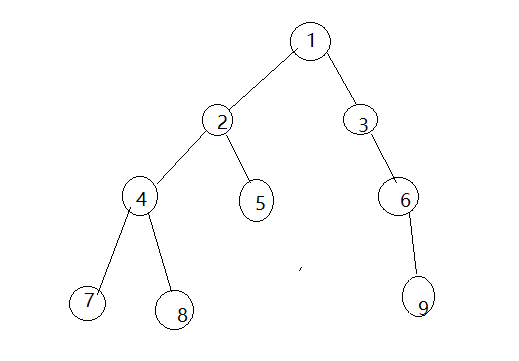
更加容易理解的二分图:
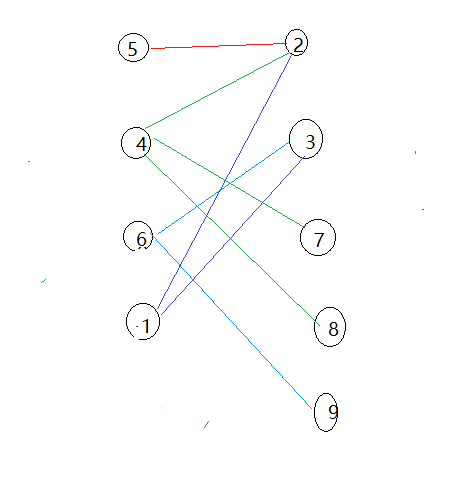
二分图的几个性质:
1)二分图的最大匹配数等于最小覆盖数,即求最少的点使得每条边都至少和其中的一个点相关联,很显然直接取最大匹配的一段节点即可。
2)二分图的独立数等于顶点数减去最大匹配数,很显然的把最大匹配两端的点都从顶点集中去掉这个时候剩余的点是独立集,这是|V|-2*|M|,同时必然可以从每条匹配边的两端取一个点加入独立集并且保持其独立集性质。
3)DAG的最小路径覆盖,将每个点拆点后作最大匹配,结果为n-m,求具体路径的时候顺着匹配边走就可以,匹配边i→j’,j→k’,k→l’….构成一条有向路径。
4)最大匹配数=左边匹配点+右边未匹配点。因为在最大匹配集中的任意一条边,如果他的左边没标记,右边被标记了,那么我们就可找到一条新的增广路,所以每一条边都至少被一个点覆盖。
5)最小边覆盖=图中点的个数-最大匹配数=最大独立集。
有了二分图与图论基础知识点,我们来看一下我们怎么去判断一个二分图!
染色法判定二分图
我们找到无向二分图本质上就是一种不存在奇数环的图,使用染色法就可以进行快速判定。
方法步骤:
首先随意选取一个未染色的点进行染色,然后尝试将其相邻的点染成相反的颜色。如果邻接点已经被染色并且现有的染色与它应该被染的颜色不同,那么就说明不是二分图。而如果全部顺利染色完毕,则说明是二分图。染色结束后的情况(记录在数组中)便将图中的所有节点分为了两个部分,即为二分图的两个点集。
图解
我们来看一下具体过程:
- 1.随意选取点1未染色的点进行染色
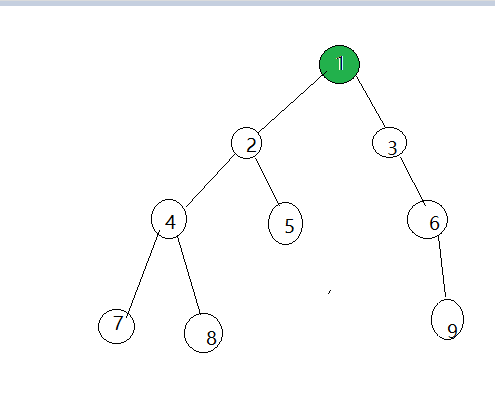
- 2.扫描与他相邻的点2,3,染成相反对颜色
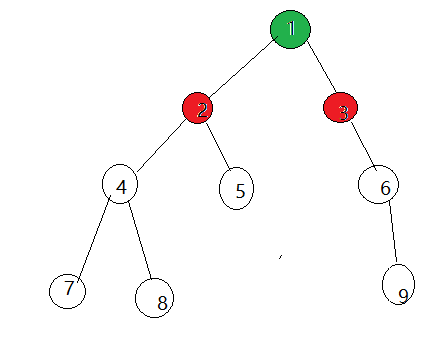
- 3.枚举每一条边
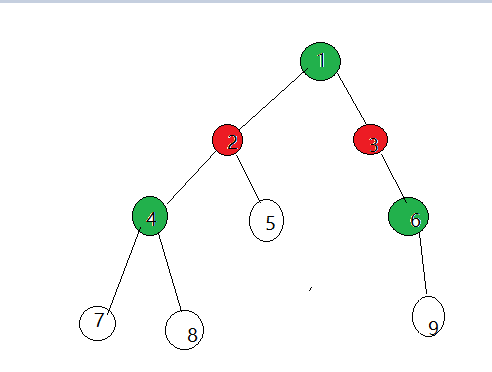
- 4.邻接点已经被染色并且现有的染色与它应该被染的颜色不同,那么就说明不是二分图。而如果全部顺利染色完毕,则说明是二分图
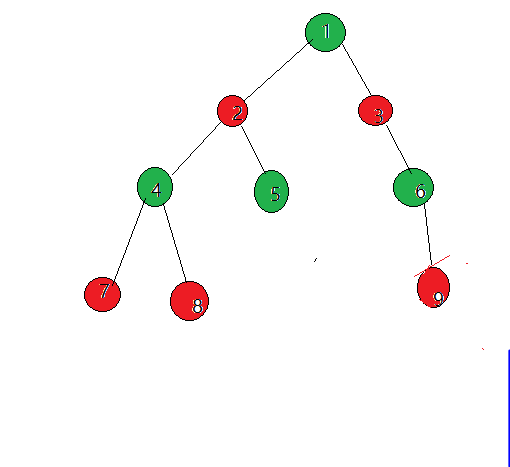
实现方式(BFS/DFS)
vector<int> g[maxn];//邻接表
int color[maxn];//1,2分别代表绿色和红色,0表示还没着色,调用前要把color数组初始化为0
bool bipartite(int u) {//判断结点u所在的联通分量是否为二分图
for (int i = 0; i < g[u].size(); ++i) {
int v = g[u][i];//枚举每条边(u,v)
if (color[v] && color[u] == color[v]) return false;//结点v已经着色,且和结点u颜色冲突
if (0 == color[v]) {
color[v] = 3 - color[u];//给结点v着与结点u相反的颜色
if (!bipartite(v)) return false;
}
}
return true;
}
改写成BFS,这样搜索不会造成栈溢出,变量的意义与之前的相同
vector<int> g[maxn];
int color[maxn];
bool bfs() {
for (int i = 1; i <= n; ++i) {
if (g[i].size() > 0 && 0 == color[i]) {
queue<int> que;
while (!que.empty()) que.pop();
que.push(i);
while (!que.empty()) {
int u = que.front();
que.pop();
for (int i = 0; i < g[u].size(); ++i) {
int v = g[u][i];
if (color[v] && color[v] == color[u]) return false;
if (color[v] == 0) {
color[v] = 3 - color[u];
que.push(v);
}
}
}
}
}
return true;
}
例题 例题链接
AC代码:(水题)
题意:就是让我们去判别一个图是否是一个二分图!!
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=100010,M=200010;
int n,m;
int h[N],e[M],ne[M],idx;
int color[N];
bool dfs(int u,int c){
color[u]=c;
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if(!color[j])
{
if(!dfs(j,3-c))return false;
}
else if (color[j]==c)return false;
}
return true;
}
int add(int a,int b){
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
int main(){
cin>>n>>m;
memset(h,-1,sizeof h);
while(m--){
int a,b;
cin>>a>>b;
add(a,b),add(b,a);
}
bool flag=true;
for(int i=1;i<=n;i++){
if(!color[i]){
if(!dfs(i,1)){
flag=false;
break;
}
}
}
if(flag)puts("Yes");
else puts("No");
return 0;
}
我们已经基本解决一个二分图是不是的问题!我们现在来看一下异性建立恋爱关系的问题!!
匈牙利算法(匹配问题)
对于二分图匹配问题,我们来看一个特殊的问题—最大匹配问题(特殊的最大流问题)!!一般匹配问题于其方法类似
最大匹配:求解二分图最大匹配问题的一个算法是匈牙利算法,为了进行解释,首先引入两个定义:
交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
增广路:从一个未匹配点出发,并且以一个未匹配点结束的交替路称为增广路。
增广路有一个重要性质:路径上的非匹配边比匹配边多一条。因此,为了改进现有匹配以获得更大的匹配,我们只需要找出一条合法的增广路,并把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边,所以这样做不会破坏匹配的性质。交换后,图中的匹配边数目就会比原来增加1条,也就是完成了一次改进。重复这样的过程,直到找不到一条增广路为止,此时得到的匹配即为二分图的最大匹配。寻找增广路的算法使用DFS实现出来极其简洁优雅,函数DFS()返回由某一未匹配节点开始的路径是否为增广路。
为什么我们要去找增广路呢?
因为接下来要讲的匈牙利算法就是去寻找增广路而求出最大匹配数的(一句废话),对于求二分图最大匹配的算法可以用网络流去跑一个最大流求解,还可以用二分图的常见算法匈牙利算法,这里我就只讲一下匈牙利算法,这个算法的核心就是去找未匹配的点,然后从这个点出发去寻找增广路,因为增广路有几个主要的特点:
- 增广路有奇数条边 。
- 路径上的点一定是一个在X边,一个在Y边,交错出现。
- 起点和终点都是目前还没有配对的点。
- 未匹配边的数量比匹配边的数量多1。
匈牙利算法要点:
- 1从左边第 1 个顶点开始,挑选未匹配点进行搜索,寻找增广路。
> 1)如果经过一个未匹配点,说明寻找成功。更新路径信息,匹配边数 +1,停止搜索。
> 2)如果一直没有找到增广路,则不再从这个点开始搜索。事实上,此时搜索后会形成一棵匈牙利树。我们可以永久性地把它从图中删去,而不影响结果。- 2由于找到增广路之后需要沿着路径更新匹配,所以我们需要一个结构来记录路径上的点。DFS 版本通过函数调用隐式地使用一个栈,而 BFS 版本使用 prev 数组。
实现
下面先以一个简单图为例来演示一下算法的整个流程,最好对照着代码实现来看。首先我们有一个由6个节点组成的二分图,上下各有三个节点以如图所示方式连接,我们分别称之为“上1-3点”和“下1-3点”。我们约定建图时的加边顺序为从上三个节点向下三个节点连有向边;约定以Match数组记录其中下三点所对应的匹配点,这样如果Match中某个节点的值为undefined,说明这个节点还未被匹配。
所以问题来了:
- 为什么我们只从一个点集(也就是上侧)开始DFS?
- 为什么我们研究的是无向二分图的最大匹配,但在这里加的却是有向边,只从一侧连向另外一侧?
- 为什么上下节点的编号可以相同却不影响结果?
这两个问题将在下文给出分析。
两个问题将在下文给出分析。
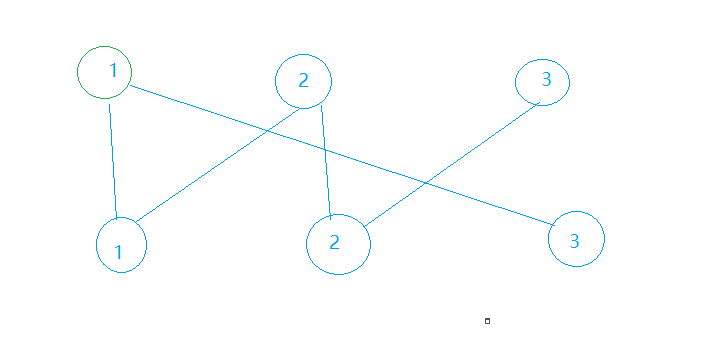
我们要遍历上侧点集进行DFS寻找增广路。首先我们从上1节点进行DFS,走到了下1节点,此时下1节点的Match[1]为undefined,说明这两个点可以匹配,于是记录Match[1] = 1并返回True,此时DFS就结束了,总匹配数为1。
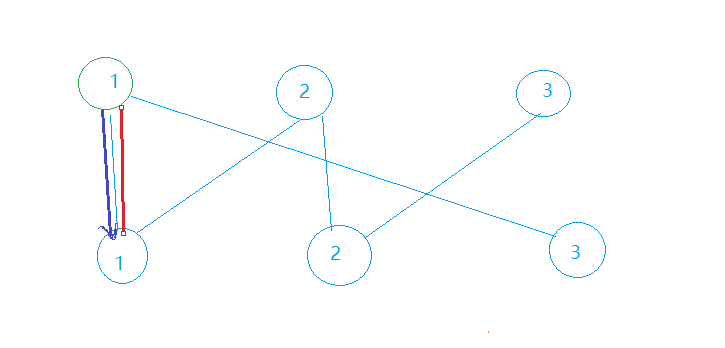
同理,从上2节点进行DFS,记录Match[2] = 2后返回,总匹配数加1后为2。
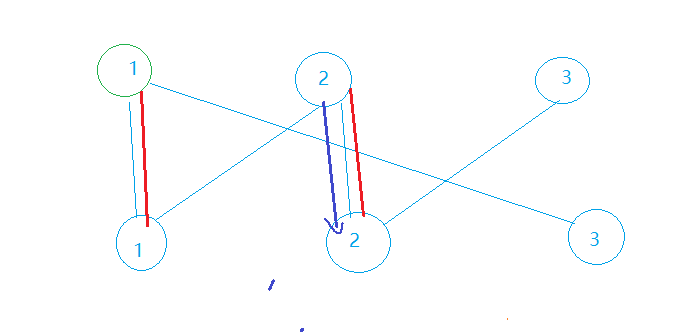
下面就到了匈牙利算法的核心部分,寻找增广路并进行增广的过程:
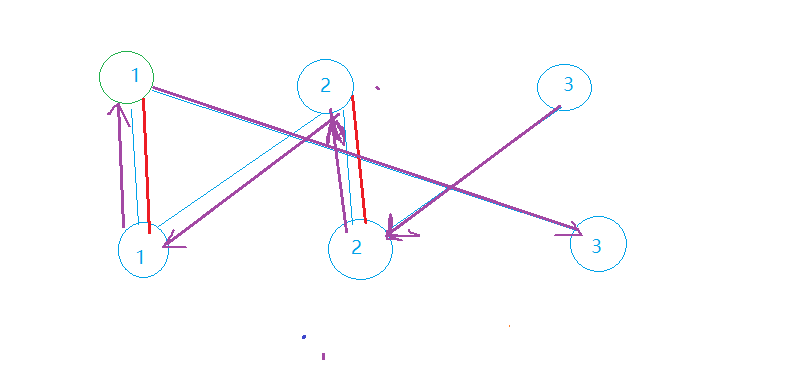
首先我们可以看到,从上3节点进行DFS,第一次走到了下2节点。显然这个节点被红边所连接,是一个已匹配点,于是就从下2节点所对应的匹配节点——上2节点开始DFS。从上2节点进行DFS时,由于下2节点已经访问过不能再走,所以就走到了下1节点。下1节点仍然是已匹配点,于是从它的对应点上1节点再进行DFS。又因为下1节点已经访问过,所以此次从上1节点的DFS只能走到下3节点。终于,下3节点是一个未匹配点,我们找到了一条增广路,返回True之后总匹配数加1变成了3,即为这个图的最大匹配。
将匹配边与非匹配边交换的代码实现非常简单,在回溯的过程中加一句Match[v] = u即可。这样做的合法性在于,这句代码第一次执行是在找到了增广路的结束点,即未配对点时,然后会不断回溯更新。在这个例子中,我们总共进行了三次递归调用,即在递归终点处存在一个三层的函数调用栈。当DFS走到下3节点时确定找到了一条增广路,这时在调用栈顶,于是将未配对的下3节点与上1节点配对(因为是从上1节点DFS过来的);然后回溯并退栈一层之后,由于上1节点是从下1节点的配对点Match[1]执行DFS(Match[v])来调用的,所以函数调用栈中u为2而v为1,下1节点会与上2节点配对;同理,下2节点会与上3节点配对。这样最终得到的最大匹配就如下所示了:
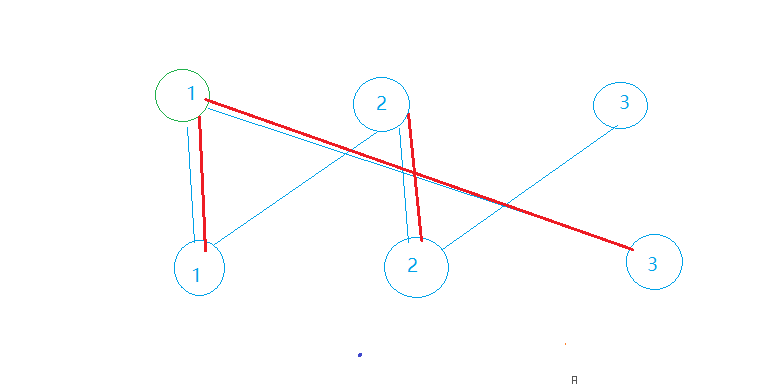
通过上述过程我们可以看出,只需要用一个Match数组就可以记录下层节点对应上层节点的匹配关系。并且只要调用DFS寻找增广路时是以上层节点编号作为参数,那么每次递归调用时传递的参数就都是指上层节点的编号,也就是说遍历边时只存在由上层节点走向下层节点的走法。因此判断点能不能走的时候也只需要判断下层节点是不是走过(是否已经加入了增广路)即可。由对称性可知,如果选择从下层节点出发寻找增广路,那么每次函数调用只会以下层节点的编号作为参数,情况是一样的。
这样梳理整个流程后,我们就回答了上述的问题:
增广路是对称的——以未覆盖点开始,同样以未覆盖点结束;如果我们从一侧未覆盖点进行DFS时找不到增广路,那么从另外一侧再DFS当然也一样找不到。由于在DFS寻找增广路的过程中只用到了从一个点集走向另外一个点集的边,因此单向加有向边即可。双向加边当然也可以,不过这样就相当于求了两次最大匹配,结果应该除以2。而当我们不需要输出具体的匹配方案,只需要输出最大匹配数时,两个点集中节点的编号完全可以存在重合,因为每次DFS调用时的参数(节点编号)都只是属于其中一个点集的。这样做会带来一个好处:每次DFS求增广路前必须清空标记数组,如果节点编号重合,就可以减小这个开销,数组可以减少一半的大小。
例题 例题链接
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=510,M=100010;
int n1,n2,m;
int h[N],e[M],ne[M],idx;
int match[N];
void add(int a,int b){
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
bool st[N];
int find(int x){
for(int i=h[x];i!=-1;i=ne[i]){
int j=e[i];
if(!st[j]){
st[j]=true;
if(match[j]==0||find(match[j]))
{
match[j]=x;
return true;
}
}
}
return false;
}
int main(){
cin>>n1>>n2>>m;
memset(h,-1,sizeof h);
while(m--){
int a,b;
cin>>a>>b;
add(a,b);
}
int res=0;
for(int i=1;i<=n1;i++)
{
memset(st,false,sizeof st);
if(find(i))res++;
}
cout<<res<<endl;
return 0;
}
小结
对于二分图,其实就是老师说的一个月老的游戏,当然我们先理解二分图的一些基本知识点,对于用染色法去解决二分图判定问题,其实就是图论搜索的扩展知识点,当然我们选择用BFS/DFS要看题目的数据大小,而匈牙利算法的核心就是增广路径,你如何去满足异性匹配最大值,还有就是的图用什么去存储,而且他们带来的时间复杂度是不一样的
我们来看一下这个分析:
| 找一次增广路径的时间 | 总时间 | 空间复杂度 | |
|---|---|---|---|
| 邻接矩阵 | O(n^2) | O(n^3) | O(n^2) |
| 邻接表 | O( n+m) | O(nm) | O( m+n) |
当然对于二分图问题,这是入门,例如网络流问题等,由于问题太多整理资料分析过于庞大,所以我将他们分为三节,后续会在图论小知识四五中介绍,感谢你的阅读,希望有所收获,当然有问题请及时体现作者,以避免其他人的错误理解!!
yxc老师的模板
注意:
前面的二分图实现我们用来动态数组去实现邻接表,雪菜老师用的是静态!!!(所以不要产生疑惑)
染色法判别二分图
时间复杂度是 O(n+m)O(n+m), nn 表示点数,mm 表示边数
int n; // n表示点数
int h[N], e[M], ne[M], idx; // 邻接表存储图
int color[N]; // 表示每个点的颜色,-1表示为染色,0表示白色,1表示黑色
// 参数:u表示当前节点,father表示当前节点的父节点(防止向树根遍历),c表示当前点的颜色
bool dfs(int u, int father, int c)
{
color[u] = c;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (color[j] == -1)
{
if (!dfs(j, u, !c)) return false;
}
else if (color[j] == c) return false;
}
return true;
}
bool check()
{
memset(color, -1, sizeof color);
bool flag = true;
for (int i = 1; i <= n; i ++ )
if (color[i] == -1)
if (!dfs(i, -1, 0))
{
flag = false;
break;
}
return flag;
}
匈牙利算法
时间复杂度是 O(nm)O(nm), nn 表示点数,mm 表示边数
int n; // n表示点数
int h[N], e[M], ne[M], idx; // 邻接表存储所有边
int match[N]; // 存储每个点当前匹配的点
bool st[N]; // 表示每个点是否已经被遍历过
bool find(int x)
{
for (int i = h[x]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true;
if (match[j] == 0 || find(match[j]))
{
match[j] = x;
return true;
}
}
}
return false;
}
// 求最大匹配数
int res = 0;
for (int i = 1; i <= n; i ++ )
{
memset(st, false, sizeof st);
if (find(i)) res ++ ;
}
作者:yxc
链接:https://www.acwing.com/blog/content/405/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。


# 大佬!Orz
选中一下看看是啥能否帮忙看一下,我是按照你和yxc的思路写的,但是BFS和DFS在n=10000,m=100000的时候都超时了
#include<stdio.h> #include<cstring> #include<iostream> #include<queue> using namespace std; const int N = 100010,M = 100010; int h[N],e[N],ne[N],idx = 0; int st[N];//0代表未染色,1代表颜色1,2代表颜色2 bool res = true; void add(int from,int to) { e[idx] = to; ne[idx] = h[from]; h[from] = idx ++; } bool bfs(int u) { queue<int> q; q.push(u); st[u] = 1; while(!q.empty()) { int p = q.front(),color = st[p],next_color = 3 - color; q.pop(); for(int i = h[p] ; i != -1 ; i = ne[i]) { int j = e[i]; if(st[j] == color) return false; else if(st[j] == 0) { st[j] = next_color; q.push(j); } } } return true; } bool dfs(int u,int c) { st[u] = c; for(int i = h[u] ; i != -1 ; i = ne[i]) { int j = e[i]; if(st[j] == c) return false; else if(st[j] == 0 && !dfs(j,3 - c)) return false; } return true; } int main() { int n,m,from,to; scanf("%d %d",&n,&m); memset(h,-1,sizeof(h)); memset(st,0,sizeof(st)); for(int i = 0 ; i < m ; i ++) { scanf("%d %d",&from,&to); add(from,to); add(to,from); } for(int i = 1 ; i <= n ; i ++) { if(st[i] == 0) { if(dfs(i,1) == false) { res = false; break; } } } if(res) printf("Yes"); else printf("No"); return 0; }边的数组开小啦
不错啊hh 很棒!